Синквейн как составить по математике: Синквейн к слову «Математика»

Мастер- класс « Синквейн на уроках математики»

Сценарий мастер- класса « Синквейн на уроках математики».

1. Актуальность выбранной темы

Математика.
Элементарная, высшая.
Изучает, рассчитывает, описывает.
Наука о количественных отношениях.
Числа.

Математика.
Вычислительная, дискретная.
Вычитает, умножает, делит.
Царица всех наук.
Действие.

Математика.
Сложная, полезная.
Пополняет, обучает, тренирует.
Порой не каждому дается.
Ум.

Речь пойдет о синквейне.

Синквейн используют преподаватели разных предметов. А чем наш хуже?

  Важнейшая задача цивилизации — научить человека мыслить»,- писал Т. Эдисон

Переход образования на обучение по Федеральным государственным Стандартам второго поколения требует от педагогов абсолютно нового подхода к организации обучения.

Для этого необходимы новые педагогические технологии, эффективные формы организации образовательного процесса, активные методы обучения.

На любом уроке учащиеся получают информацию, знакомятся с новыми терминами, учатся делать выводы, искать взаимосвязи. Для прочного усвоения знаний, отработки умений и приобретения конкретных навыков учащимся необходимо иметь способность резюмировать информацию, излагать сложные идеи, чувства и представления в нескольких словах. Это требует вдумчивой рефлексии, основанной на богатом понятийном запасе и смысле. Но как развить такие важные умения? Ответ на данный вопрос нашла совершенно случайно и там, где меньше всего этого ожидала! В этом мне помог Синквейн.

Цель сегодняшнего мастер-класса: создание оптимальной среды, позволяющей участникам мастер-класса за короткое время погрузиться в сущность представляемого опыта, оценить возможность использования представленного метода в собственной практике.

Задачи:

познакомить коллег с приёмом технологии критического мышления через чтение ; пропагандировать использование синквейна в урочной и внеурочной деятельности;

организовать профессионально-педагогическое общение по существу представленного опыта;

привлечь педагогов к участию в целенаправленном создании нового опыта профессионального взаимодействия.  

2. Начало образовательного мероприятия 
Начать урок можно необычно , предложив ученикам поздороваться глазами. 

Упражнение «Поздоровайся глазами» 
Цель – положительный настрой на работу, установление контакта между учениками.

— Уважаемые коллеги, давайте мы тоже начнём наш мастер-класс с этого упражнения.

— Сейчас я с каждым из вас поздороваюсь. Но поздороваюсь не словами, а молча — глазами. При этом постарайтесь глазами показать, какое у вас сегодня настроение.

-Вам придется работать в группах, а в отличии от учеников вы видитесь редко или может быть даже не знакомы, то сейчас я предлагаю вам познакомиться поближе друг с другом. Для этого я попрошу вас стать лицом друг к другу в два ряда:

1.Познакомиться, начав со слов «Меня зовут и рассказать о себе..» (поменяться ролями)

2.Поменяться местами, и начать со слов «Я счастлив с тобой общаться..»

3. Поменяться местами, и начать со слов «Я тебе желаю. ..»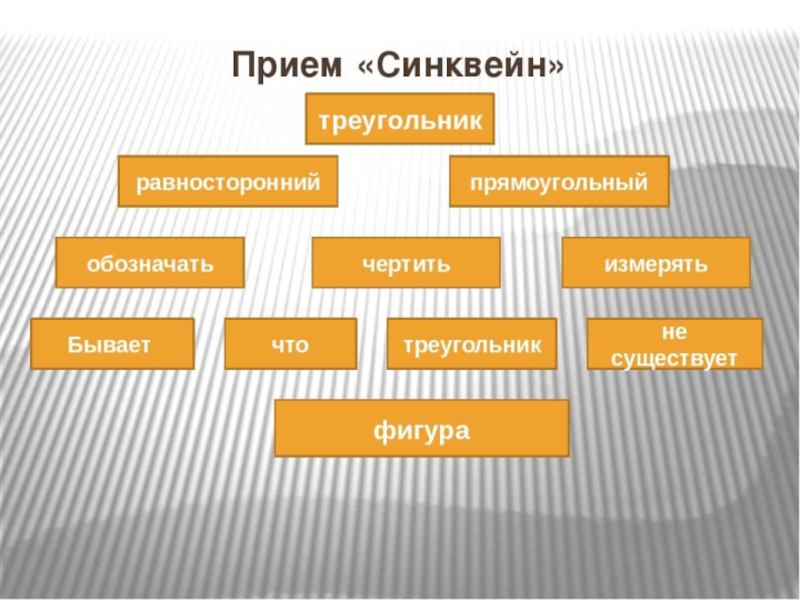

3. Выяснение ожиданий и опасений слушателей мастер-класса

-Для выяснения образовательных целей учеников, их ожиданий и опасений можно использовать следующий метод: 
Метод «Фруктовый сад» 
Учителю этот метод позволит лучше понять класс и каждого ученика, полученные материалы можно использовать при подготовке и проведении уроков (внеклассных мероприятий) для обеспечения личностно-ориентированного подхода. 

Ученикам данный метод позволит более четко определиться со своими образовательными целями, озвучить свои ожидания и опасения, с тем, чтобы педагоги могли их знать и учитывать в образовательном процессе.

Оборудование: заранее готовятся два больших плаката с нарисованным на каждом из них деревом. Одно дерево подписано «Яблоня», второе – «Лимонное дерево». Обучающимся раздаются также заранее вырезанные из бумаги крупные яблоки и лимоны. (Слайд 3)

— Уважаемые коллеги, предлагаю на яблоках записать свои ожидания от мастер-класса, а опасения на лимонах.

— Зачитайте вслух свои ответы. (По желанию).

4. Постановка задач мастер-класса

Задачи:

• познакомить коллег с приёмом технологии критического мышления через чтение ; пропагандировать использование синквейна в урочной и внеурочной деятельности;

• организовать профессионально-педагогическое общение по существу представленного опыта;

• привлечь педагогов к участию в целенаправленном создании нового опыта профессионального взаимодействия.

5. Презентации учебного материала 
Метод «Пометки на полях».

Следующий метод «Пометки на полях» или . Он позволяет   ученику отслеживать свое понимание прочитанного задания или текста. Технически он достаточно прост. Учеников надо познакомить с маркировочными знаками и предложить им по мере чтения ставить их карандашом на полях статьи учебника или специально подобранного текста. Помечать следует,  отдельные задания или предложения в тексте.

Пометки должны быть следующие (Слайд 8)

Данный метод обязывает ученика не просто читать, а вчитываться в задание, в текст, отслеживать собственное понимание в процессе чтения. Использование маркировочных знаков позволяет соотносить новую информацию с имеющимися знаниями.

Метод «Написание синквейна»

Что же такое синквейн?

Изначально синквейн возник в США как стихотворная форма. Разработала его американская поэтесса Аделаида Крэпси, опираясь на знакомство с японскими силлабическими миниатюрами хокку и танка. Традиционный синквейн состоит из пяти строк и основан на подсчёте слогов в каждом его стихе. Если интересно, то его слоговая структура – 2-4-6-8-2, всего 22 слога. Авторы, развивавшие стихотворную форму в дальнейшем, предложили ряд её вариаций: обратный синквейн, зеркальный, «бабочка», корона и даже гирлянда синквейнов.

Но нас, как учителей-предметников, будет интересовать дидактический синквейн – приём технологии критического мышления через чтение и письмо.

Дидактический синквейн

• 1 строка—тема синквейна, заключает в себе одно слово (обычно существительное или местоимение), которое обозначает объект или предмет, о котором пойдет речь.

• 2 строка—два слова (чаще всего прилагательные или причастия), они дают описание признаков и свойств выбранного в синквейне предмета или объекта.

• 3 строка—образована тремя глаголами или деепричастиями, описывающими характерные свойства объекта.

• 4 строка—фраза из четырех слов, выражающая личное отношение автора синквейна к описываемому предмету или объекту.( На четвертой строчке размещается целая фраза. Это может быть крылатое выражение, чувство, цитата или составленная учеником предложение в контексте темы)

• 5 строка—одно слово—резюме, характеризующее суть предмета или объекта. (Последняя строчка — это слово-синоним, своё отношение к данной теме, чувство или сравнение)

В этом случае текст основывается не на слоговой зависимости, а на содержательной и синтаксической заданности каждой строки. Чёткое соблюдение правил написания синквейна не обязательно. Например, для улучшения текста в четвёртой строке можно использовать три или пять слов, а в пятой – два слова. Возможны варианты использования и других частей речи.

Синквейн — это приём технологии развития критического мышления на уроках . Написание синквейна является формой свободного творчества, требующей от автора умения находить в информационном материале наиболее существенные элементы, делать выводы и кратко их формулировать. Относительная простота построения синквейна позволяет быстро получить результат. Эта работа требует вдумчивой рефлексии, основанной на богатом понятийном запасе, а также развитого образного мышления. Метод эффективен как при работе с отстающими, так и при работе с одарёнными детьми. Каждый ребёнок имеет реальную возможность стать успешным, почувствовать радость от процесса познания. А это в нашей работе самое главное.

В методике синквейн является быстрым, эффективным инструментом для анализа, синтеза и обобщения понятия и информации. Он учит осмысленно использовать понятия и определять своё отношение к рассматриваемой проблеме, используя всего пять строк. Ребёнок на основе больших объёмов информации, вырабатывая свою способность к анализу, составляет относительно небольшой текст. Составление этого текста требует сравнительно небольших временных затрат, хотя и имеет жёсткие рамки по форме изложения.

Математика – сложный предмет, не всем она даётся, поэтому не все любят её. Особенно часто приходится сталкиваться с проблемой непонимания у детей гуманитарного склада ума. Их надо заинтересовать. Это сложно. А вот написание синквейна требует от составителя реализации практически всех его личностных способностей: интеллектуальных, творческих, образных.

С точки зрения педагогики, процедура составления синквейна позволяет гармонично сочетать элементы всех трёх основных образовательных походов: информационного, деятельностного и личностно-ориентированного.

6. Релаксация

Не стоит забывать о восстанавливающей силе релаксации на уроке. Ведь иногда нескольких минут достаточно, чтобы встряхнуться, весело и активно расслабиться, восстановить энергию. Активные методы релаксации позволят сделать это, не выходя из класса. 

Упражнение «Четыре стихии» (Слайд 10)

(Чистякова М.И. Психогимнастика. М., 1995, с. 66)

— Упражнение называется «Четыре стихии». Это земля, вода, воздух, огонь. Если я скажу «земля» — вы приседаете на корточки и дотрагиваетесь руками до пола. Если я скажу «вода» — вы вытягиваете руки вперед и совершаете плавательные движения. Если скажу «воздух» — вы поднимаетесь на носочки и поднимаете руки вверх. Если я скажу «огонь» — вы вращаете руками в локтевых и лучезапястных суставах. Выполняем.

Как можно использовать этот приём в практике?

Во-первых, можно составлять текст как в школе, на уроке (я уже упоминала, что времени этот вид работы требует немного), так и дома, в качестве домашнего задания. Дети могут выполнять его как индивидуальное задание или как дополнительное к основному.

1.предмет 
2.базовый, профильный
3.учит вычислять, строить, анализировать
4.царица всех наук
5. математика

Во-вторых, работать над составлением синквейна можно как самостоятельно, так и в паре и даже в группе. Рассмотрев какой-либо теоретический материал на уроке, можно предложить в качестве рефлексии составить синквейн вдвоём. Если в паре оказываются учащиеся с разными способностями ( а как правило так и происходит), то более сильный ученик, используя посильную поддержку второго, анализирует изученное. Более сложной является работа в группе. Здесь кроме интеллектуальных способностей ребёнок должен проявить и коммуникативные.

В-третьих, использовать данный приём можно как для анализа достаточно узкого понятия (например, при рассмотрении понятия «Смежные углы»), так и при изучении достаточно объёмного материала, например, изучаемого раздела геометрии. Можно дать задание в качестве творческого.

1.Смежные углы.
2. разные, граничащие
3. Чертим, измеряем, вычисляем и знаем,
4. Что сумма их равна 180⁰.
5. Теорема.

1.наука

2.древняя, нужная

3.измеряем,строим, рассчитываем

4.возникла из практической деятельности людей и занимается изучением геометрических фигур

5.геометрия

В-четвёртых, можно придумать огромное количество способов работы с готовым синквейном. Например, можно составить краткий рассказ на заданную тему, используя подготовленный дома синквейн как подсказку. Можно, используя все свои знания по теме, внести коррекцию и совершенствовать текст, созданный товарищем, или текст с сознательно, запланировано сделанными ошибками. Наконец, можно учиться определять тему синквейна при отсутствующей части, к примеру, без первой строчки.

Давайте попробуем стать учениками 6,11 классов и составить синквейн по тем понятиям, как которые рассматривались на открытых уроках.

1. Дроби 
   2. Правильные, неправильные. 
   3. Делили, переворачивали, умножали. 
   4. делимое умножить на дробь обратную делителю
   5. Правило 

2. 1.Проценты 
   2.Сложные, интересные, увлекательные 
   3.Превращаем, вычисляем, применяем 
   4.Они выражают снижение и повышение цен 
   5.Необходимые

Чтобы вам было интересно, я предлагаю немного поиграть. Попробуйте догадаться по деформированному тексту, на какую тему был составлен синквейн.

1.
2. Строгая, логичная.
3. Строим, доказываем, вычисляем.
4. Квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.
5. Прямоугольный треугольник.

1.
2. Точная, практичная.
3. Доказываем, учим, считаем.

4. Строим мы угол прямой, 
Катеты на нём отмечаем,
А квадрат гипотенузы – 
Легко вычисляем:

с²= а² + в²

5. Красота!

1. 

2. Необходимая, важная.
3. Строим, учим, измеряем.

4. Сумму квадратов катетов – мы знаем, 
Квадрат гипотенузы – вычисляем, 
Корень квадратный из неё извлекаем
И результат — всегда получаем.

5. “Пифагоровы штаны на все стороны равны!”

1. Экзамен.
2. Строгий, трудный.
3. Проверяет, доказывает, подтверждает

4. Что ты знаешь, а чего не знаешь,
И какую оценку за это получаешь.

5. Испытание

1. Прямые. 
2. Пересекающиеся, параллельные. 
3. чертим, обозначаем, совмещаем. 
4. они не имеют ни начала, ни конца. 
5. бесконечность 

Согласитесь, что использование этого приёма на уроках математики оправдано. Чем разнообразнее формы и методы нашей с вами работы, тем больше шанс, что ребёнку на уроке не будет скучно, что каждый день принесёт ему радость пусть маленького, но открытия. Надеемся, что открытие сегодня сделал и каждый из вас. Желаем вам дальнейших творческих успехов в нашем нелёгком, но благодарном труде, дорогие коллеги!

Рефлексия. Подведение итогов мастер-класса.

— Подводя итог нашего мастер-класса, вернёмся к «Фруктовому саду». Вспомните, какие ожидания и опасения были у вас в начале мастер-класса. Определите для себя, оправдались ли они.

— И в заключении хочу пожелать всем успехов в нашей работе и напомнить, что больше всего дети утомляются в бездействии.

Мастер-класс.

Волнующий, интересный.

Учит, вдохновляет, показывает.

Мысли будоражит, уверенность пробуждает.

Полезно.

Приложения

Примеры синквейнов:

1. Теорема Пифагора
2. Строгая, логичная.
3. Строим, доказываем, вычисляем.
4. Квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.
5. Прямоугольный треугольник.

(Никонкова Анастасия, 8*а класс)

1. Теорема Пифагора
2. Точная, практичная.
3. Доказываем, учим, считаем.

4.

Строим мы угол прямой, 
Катеты на нём отмечаем,
А квадрат гипотенузы – 
Легко вычисляем:

с²= а² + в²

5. Красота!

(Удовина Руслана, 8*а класс)

1.  Теорема Пифагора
2. Необходимая, важная.
3. Строим, учим, измеряем.

4.

Сумму квадратов катетов – мы знаем, 
Квадрат гипотенузы – вычисляем, 
Корень квадратный из неё извлекаем
И результат — всегда получаем.

5. “Пифагоровы штаны на все стороны равны!”

(Удовина Руслана, 8*а класс)

1. Египетский треугольник.
2. Нужный, точный. 
3. Показывает, определяет, помогает

4.

Три, четыре и ровно – пять
Прямой угол нам отыскать:

5²= 4² + 3²

5. Практика!

(Никонкова Анастасия, 8*а класс)

1. Прямые.
2. Пересекающиеся, параллельные.
3. Строим, проектируем, совмещаем.
4. Все прямые не имеют ни начала, ни конца.
5. Это бесконечность!

(Гущин Владимир, 7*а класс)

1. Смежные углы.
2. Красивы, но не всегда равны.
3. Чертим, измеряем и знаем,
4. Что сумма их равна 180⁰.
5. Теорема.

(Ткачёва Алина, 7*а класс)

1. Контрольная работа.
2. Интересная, понятная.
3. Пишем, строим, вычисляем.
4. Тетрадь для контрольных работ.
5. Математика.

(Казаков Артём , 5*а класс)

1. Экзамен.
2. Строгий, трудный.
3. Проверяет, доказывает, подтверждает

4.

Что ты знаешь, а чего не знаешь,
И какую оценку за это получаешь.

5. Подведение итогов, испытание.

В одной притче говорится: “Жил мудрец, который знал всё.

Один человек захотел доказать, что мудрец знает не всё. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мёртвая или живая?” А сам думает: “Скажет живая – я ее умерщвлю, скажет мёртвая – выпущу”. Мудрец, подумав, ответил: “Всё в твоих руках”. В наших руках, чтобы ребенок чувствовал себя любимым Слайд 4нужным Слайд 5
а главное, успешным.