Умозаключения виды: Определение и структура умозаключения. Виды умозаключений -Логика

§ 1. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. ВИДЫ УМОЗАКЛЮЧЕНИЙ. Логика: учебник для юридических вузов

§ 1. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. ВИДЫ УМОЗАКЛЮЧЕНИЙ. Логика: учебник для юридических вузов

ВикиЧтение

Логика: учебник для юридических вузов
Кириллов Вячеслав Иванович

Содержание

§ 1. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. ВИДЫ УМОЗАКЛЮЧЕНИЙ

В процессе познания мы приобретаем новые знания. Некоторые из них — непосредственно, в результате воздействия предметов внешнего мира на органы чувств. Но большую часть знаний — путем выведения новых знаний из знаний уже имеющихся. Эти знания называются опосредствованными, или выводными.

Логической формой получения выводных знаний является умозаключение.

Умозаключение — это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение.

Умозаключение состоит из посылок, заключения и вывода. Посылками умозаключения называют исходные суждения, из которых выводится новое суждение. Заключением называется новое суждение, полученное логическим путем из посылок. Логический переход от посылок к заключению называется выводом.

Например, из посылок «Преступление наказуемо» и «Мошенничество — преступление» следует заключение «Мошенничество наказуемо». Заключение получено благодаря связи посылок общим понятием «преступление».

При анализе умозаключения посылки и заключение принято записывать следующим образом:

} посылки.

Мошенничество наказуемо — заключение.

Посылки записываются над чертой, заключение — под чертой.

При содержательной связи между посылками заключение будет истинным, если соблюдаются два условия: во-первых, исходные суждения — посылки умозаключения должны быть истинными; во-вторых, в процессе рассуждения следует соблюдать правила вывода, которые обусловливают логическую правильность умозаключения.

Умозаключения делятся на следующие виды.

1. В зависимости от строгости правил вывода различают демонстративные (необходимые) и недемонстративные (правдоподобные) умозаключения. В демонстративных умозаключениях заключение с необходимостью следует из посылок, т. е. логическое следование представляет собой логический закон. В недемонстративных умозаключениях правила вывода обеспечивают лишь вероятностное следование заключения из посылок.

2. По направленности логического следования, т. е. по характеру связи между знанием различной степени общности, выраженному в посылках и заключении, различают три вида умозаключений: дедуктивные (от общего знания к частному), индуктивные (от частного знания к общему), умозаключения по аналогии

(от частного знания к частному).

Эта классификация будет положена в основу дальнейшего изложения.

Рассмотрим дедуктивные умозаключения.

Дедуктивными (от латинского deductio — «выведение») называется умозаключение, в котором переход от общего знания к частному является логически необходимым.

Правила дедуктивного вывода определяются характером посылок, которые могут быть простыми (категорическими) или сложными суждениями.

3. В зависимости от количества посылок дедуктивные выводы из категорических суждений делятся на непосредственные, в которых заключение выводится из одной посылки, и опосредствованные, в которых заключение выводится из двух посылок.

Вопросы для самопроверки

1. Что такое умозаключение? Приведите определение.

2. Что называется посылкой, заключением, выводом?

3. На какие виды делятся умозаключения по строгости вывода, по

направленности логического следования, по количеству посылок?

Данный текст является ознакомительным фрагментом.

2 ГЛАВА. Понятие как форма мышления

2 ГЛАВА. Понятие как форма мышления В современной логике, особенно математической, которая ориентируется на дедуктивные, доказательные рассуждения, проблема понятия утратила то значение, которая она имела в традиционной логике. Со времен Г. Фреге понятие рассматривается

§ 1. Понятие как форма мышления

§ 1. Понятие как форма мышления Окружающий нас мир предстает перед человеком не скоплением одинаковых предметов, а как множество предметов, явлений, процессов, наделенных различными свойствами. Любые свойства, черты, состояния, отношения предме­та, которые характеризуют

Понятие как форма мышления и его структура

Понятие как форма мышления и его структура Понятие – это форма мышления, отражающая предметы в их существенных признаках.Признаком предмета называется то, в чем предметы сходны друг с другом или отличаются друг от друга. Т. о., признаки представляют собой черты, свойства

3.2. Виды умозаключений

3.2. Виды умозаключений Умозаключения, или опосредованные умозаключения делятся на три вида. Они бывают дедуктивными, индуктивными и умозаключениями по аналогии.Дедуктивные умозаключения или дедукция (от лат. deductio – выведение) – это умозаключения, в которых из общего

11. ФОРМА АРИЙСКОГО МЫШЛЕНИЯ

11. ФОРМА АРИЙСКОГО МЫШЛЕНИЯ Если нам даже здесь пришлось различать между формой и материей мышления — что было вызвано требованиями тогдашнего момента нашего исследования — то можно себе представить, как должно было пренебрежение этим формальным элементом повлиять на

§ 1. ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ

§ 1. ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ Понятие — это форма мышления, отражающая предметы в их существенных признаках. Признаком предмета называется то, в чем предметы сходны друг с другом или чем они друг от друга отличаются.Любые свойства, черты, состояния предмета, которые так

3. Содержание и форма мышления

3. Содержание и форма мышления Выясним теперь, что такое «форма мышления», которую изучает логика и которую поэтому называют еще логической формой. Это понятие является в логике одним из фундаментальных. Вот почему остановимся на нем специально.Из философии известно, что

Глава I. Понятие как форма мышления

Глава I. Понятие как форма мышления 1. Понятие и предмет Происхождение и сущность понятия1. Из следующих высказываний выделите все понятия и определите, что именно в них отражается — предмет (явление), свойство или отношение: «Земля — планета». «В России проводится

Глава I.

Суждение как форма мышления

Глава I. Суждение как форма мышления 1. Суждение и связь (отношение) предметов 1. Какие конкретно связи (отношения) между предметами действительности отражены в следующих суждениях: «Земля — планета». «Кит —не рыба, а млекопитающее». «Человек — существо

Глава I. Умозаключение как форма мышления

Глава I. Умозаключение как форма мышления 1. Умозаключение и взаимосвязь (взаимоотношение) предметов 1. Из приведенных примеров выделите умозаключения: «Таможня». «Правоохранительный орган». «Петров». «Таможня — правоохранительный орган». «Петров работает в таможне».

Глава I. Доказательство как форма мышления

Глава I. Доказательство как форма мышления 1. Доказательство и всеобщая обусловленность предметов Какова объективная основа следующего доказательства: «Поскольку римляне кремировали усопших, в распоряжении ученых было очень мало скелетов римской эпохи. Однако уже

10. Понятие как форма мышления

10. Понятие как форма мышления Понятие – это форма мышления, отражающая предметы и явления в их существенных признаках.Признаками могут быть свойства предмета, которые объединяют или отделяют предметы один от другого. Иными словами, признаки – это свойства предметов, в

44. Виды индуктивных умозаключений

44. Виды индуктивных умозаключений Первоначально следует сказать об основополагающем разделении индуктивных умозаключений. Они бывают полные и неполные.Полными называются умозаключения, в которых вывод делается на основе всестороннего изучения всей совокупности

ЛЕКЦИЯ № 5 Понятие как форма мышления

ЛЕКЦИЯ № 5 Понятие как форма мышления 1. Общая характеристика понятий Понятие — это форма мышления, отражающая предметы и явления в их существенных признаках. Как уже говорилось выше, человек воспринимает тот или иной предмет, выделяя характерные свойства (признаки)

ЛЕКЦИЯ № 15 Умозаключение. Общая характеристика дедуктивных умозаключений

ЛЕКЦИЯ № 15 Умозаключение. Общая характеристика дедуктивных умозаключений 1. Понятие умозаключения Умозаключение — это форма абстрактного мышления, посредством которой из ранее имевшейся информации выводится новая. При этом не задействуются органы чувств, т. е. весь

3. Виды индуктивных умозаключений

3. Виды индуктивных умозаключений Первоначально следует сказать об основополагающем разделении индуктивных умозаключений. Они бывают полные и неполные.Полными называются умозаключения, в которых вывод делается на основе всестороннего изучения всей совокупности

Урок 6.

Умозаключения

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

• Критерии истинности умозаключений
• Умозаключения по логическому квадрату
• Операция обращения
• Игра «Подбери ключ»
• Упражнения
• Проверочные вопросы на усвоение материала

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»

Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.

Логики записывают умозаключения следующим образом:

Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы.

В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.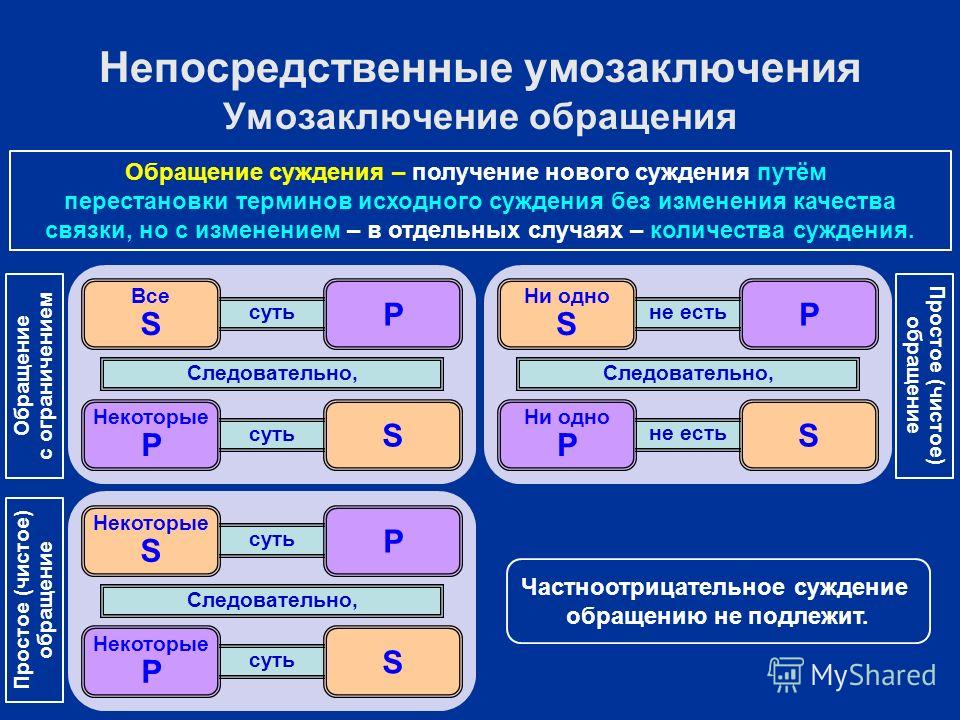

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

Умозаключения по логическому квадрату

Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

• Все S есть P
• Некоторые S есть P
• Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
• Ни один S не есть P
• Некоторые S не есть P
• Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

• Неверно, что некоторые S есть P
• Неверно, что все S есть P
• Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
• Неверно, что некоторые S не есть P
• Неверно, что все S не есть P
• Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

• Все S есть P
• Неверно, что ни один S не есть P
• Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
• Ни один S не есть P
• Неверно, что все S есть P
• Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

• Согласно этому закону правильными будут следующие умозаключения:
• Неверно, что некоторые S есть P
• Некоторые S не есть P
• Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
• Неверно, что некоторые S не есть P
• Некоторые S есть P
• Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

• Все S есть P
• Неверно, что некоторые S не есть P
• Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
• Некоторые S не есть P
• Неверно, что все S есть P
• Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
• Неверно, что все S есть P
• Некоторые S не есть P
• Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
• Неверно, что некоторые S не есть P
• Все S есть P
• Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
• Ни один S не есть P
• Неверно, что некоторые S есть P
• Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
• Некоторые S есть P
• Неверно, что ни один S не есть P
• Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
• Неверно, что ни один S не есть P
• Некоторые S есть P
• Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
• Неверно, что некоторые S есть P
• Ни один S не есть P
• Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

• Ни один S не есть P
• Ни один P не есть S
• Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
• Некоторые S есть P
• Некоторые P есть S
• Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
• Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
• Все S есть P
• Некоторые P есть S
• Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
• Ни один S не есть P
• Некоторый P не есть S
• Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
• Высказывания типа «Некоторые S не есть P» вообще не обращаются.

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Cтатистика На весь экран

Упражнения

1

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

• Все медведи на зиму залегают в спячку.
• Неверно, что все люди завистливы.
• Ни один гном не достигает роста в два метра.
• Неверно, что ни один человек не был на Северном полюсе.
• Некоторые люди никогда не видели снега.
• Некоторые автобусы ходят по расписанию.
• Неверно, что некоторые слоны летали на луну.
• Неверно, что некоторые птицы не имеют крыльев.

2

Сделайте обращения с теми, высказываниями, с которыми это возможно:

• Никто ещё не построил машину времени.
• Некоторые официанты очень назойливы.
• Все профессионалы опытны в своём деле.
• Некоторые книги не имеют твёрдой обложки.

3

Проверьте, правильно ли сделаны следующие умозаключения:

• Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
• Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
• Все люди смертны. Поэтому все смертные – это люди.
• Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
• Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
• Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Cтатистика На весь экран

Ксения Галанина

← 5 Законы и противоречия7 Силлогизмы →

5.4 Типы умозаключений — Введение в философию

Цели обучения

К концу этого раздела вы сможете:

• Дайте определение дедуктивным, индуктивным и абдуктивным выводам.
• Классифицируйте выводы как дедуктивные, индуктивные или абдуктивные.
• Объясните различные объяснительные достоинства, используемые в абдуктивных рассуждениях.

Выводы могут быть дедуктивными, индуктивными или абдуктивными. Дедуктивные выводы являются самыми сильными, потому что они могут гарантировать истинность своих выводов. Индуктивные выводы используются наиболее широко, но они не гарантируют истинности, а вместо этого позволяют делать выводы, которые, вероятно, верны. Абдуктивные умозаключения также имеют дело с вероятностью.

Дедуктивное рассуждение

Дедуктивные выводы, которые являются выводами, полученными посредством дедукции (дедуктивного рассуждения), могут гарантировать истину, поскольку они сосредоточены на структуре аргументов. Вот пример:

1. Либо ты можешь пойти в кино сегодня вечером, либо ты можешь пойти на вечеринку завтра.
2. Сегодня ты не можешь пойти в кино.
3. Итак, завтра ты можешь пойти на вечеринку.

Этот аргумент хорош, и вы, вероятно, знали, что он хорош, даже не слишком задумываясь об этом. В аргументе используется «или», что означает, что по крайней мере одно из двух утверждений, соединенных «или», должно быть истинным. Если вы обнаружите, что одно из двух утверждений, соединенных союзом «или», ложно, вы узнать , что другое утверждение истинно, используя дедукцию. Обратите внимание, что этот вывод работает независимо от того, какие утверждения. Взгляните на структуру этой формы рассуждения:

1. X или Y верно.
2. X не соответствует действительности.
3. Следовательно, Y истинно.

Заменив операторы переменными, мы получим форму исходного аргумента выше. Независимо от того, какими утверждениями вы заменяете X и Y, если эти утверждения верны, то вывод также должен быть верным. Эта распространенная форма аргумента называется дизъюнктивным силлогизмом.

Действительные дедуктивные выводы

Хороший дедуктивный вывод называется верным выводом, что означает, что его структура гарантирует истинность его заключения при условии истинности предпосылок. Обратите внимание на это определение. В определении не говорится, что действительные аргументы имеют верных выводов. Обоснованность — это свойство логических форм аргументов, и помните, что логика и истина различны. В определении говорится, что действительные аргументы имеют такую ​​форму, что если посылки верны, то и заключение должно быть верным. Вы можете проверить правильность дедуктивного вывода, проверив, ведут ли посылки к заключению. Если вывод не может быть ложным, когда посылки предполагаются истинными, то аргумент действителен.

Дедуктивное рассуждение может использовать ряд допустимых структур аргументов:

Дизъюнктивный силлогизм :

1. X или Y.
2. Не Y.
3. Следовательно, X.

Модус Поненс :

1. Если X, то Y.
2. Х.
3. Поэтому Y.

Модус Толленс :

1. Если X, то Y.
2. Не Y.
3. Следовательно, не X.

Вы видели первую форму, разделительный силлогизм, в предыдущем примере. Вторая форма, modus ponens, использует условное предложение, и если вы подумаете о уже обсуждавшихся необходимых и достаточных условиях, то справедливость этого вывода станет очевидной. Условие в посылке 1 выражает, что X достаточно для Y. Итак, если X истинно, то Y должно быть истинным. А посылка 2 утверждает, что X истинно. Таким образом, вывод (истинность Y) обязательно следует. Вы также можете использовать свои знания о необходимых и достаточных условиях, чтобы понять последнюю форму modus tollens. Помните, что в условном предложении следствие является необходимым условием. Итак, Y необходимо для X. Но посылка 2 утверждает, что Y равно 9.0029 не верно. Поскольку Y должно иметь место, если X имеет место, и нам говорят, что Y ложно, тогда мы знаем, что X также ложно. Эти три примера — лишь некоторые из многочисленных возможных верных выводов.

Неверные дедуктивные выводы

Плохой дедуктивный вывод называется неверным выводом. В неверных выводах их структура не гарантирует истинности вывода, т. е. даже если посылки верны, вывод может быть ложным. Это не означает, что вывод должно быть ложным, но мы просто не можем знать, истинно это заключение или ложно. Вот пример неверного вывода:

1. Если выпало более трех дюймов снега, школы обязаны закрыться.
2. Школы закрыты.
3. Следовательно, снега выпало более трех дюймов.

Если предпосылки этого аргумента верны (а мы предполагаем, что они верны), то снега могло или не могло быть более трех дюймов. Школы закрываются не только из-за снега, но и по многим причинам. Возможно, в школьном округе произошло отключение электроэнергии или в этом районе было объявлено предупреждение об урагане. Опять же, вы можете использовать свои знания необходимых и достаточных условий, чтобы понять, почему эта форма недействительна. Посылка 2 утверждает, что необходимое условие имеет место. Но истинность необходимого условия не гарантирует истинности достаточного условия. Условие гласит, что закрытие школ гарантируется при выпадении снега более 3 дюймов, , а не , что снег толщиной более 3 дюймов гарантирован, если школы закрыты.

Неверные дедуктивные выводы также могут принимать общие формы. Вот две распространенные недопустимые формы вывода:

Подтверждение следствия:

1. Если X, то Y.
2. г.
3. Следовательно, Х.

Отрицание антецедента:

1. Если X, то Y.
2. Не Х.
3. Следовательно, не Y.

Вы видели первую форму, подтверждающую следствие, в предыдущем примере о закрытии школ. Заблуждение называется так потому, что истинность следствия (необходимого условия) утверждается, чтобы сделать вывод об истинности предшествующего утверждения. Вторая форма, отрицающая антецедент, возникает, когда истинность антецедентного утверждения отрицается, чтобы сделать вывод, что следствие ложно. Ваше знание достаточности поможет вам понять, почему этот вывод неверен. Истинности антецедента (достаточного условия) достаточно только для того, чтобы знать истинность следствия. Но консеквент может быть истинным более чем одним способом, а это означает, что ложность достаточного условия не гарантирует, что консеквент ложен. Возвращаясь к более раннему примеру, то, что существо не является собакой, не позволяет сделать вывод, что оно не является млекопитающим, хотя для того, чтобы быть млекопитающим, достаточно быть собакой. Посмотрите видео ниже, чтобы увидеть дополнительные примеры условного мышления. Посмотрите, сможете ли вы выяснить, какой неправильный выбор структурно идентичен подтверждению следствия или отрицанию предшествующего.

видео

Задача выбора Уэйсона

Проверка дедуктивных выводов

Ранее объяснялось, что логический анализ включает в себя допущение, что посылки аргумента верны, а затем определение того, логически ли следует заключение, учитывая истинность этих посылок. Для дедуктивных аргументов, если вы можете придумать сценарий, в котором предпосылки верны, но вывод ложен, вы доказали, что аргумент недействителен. Пример дедуктивного аргумента, в котором все посылки верны, но вывод ложен, называется контрпримером. Как и контрпримеры к утверждениям, контрпримеры к аргументам — это просто примеры, которые работает счетчик до аргумент. Контрпримеры к утверждениям показывают, что утверждение ложно, а контрпримеры к дедуктивным аргументам показывают, что аргумент недействителен. Выполните приведенное ниже упражнение, чтобы лучше понять, как придумывать контрпримеры для доказательства недействительности.

Думай как философ

Используя приведенные примеры аргументов, приведите контрпример, чтобы доказать, что аргумент недействителен. Контрпример — это сценарий, в котором посылки верны, но заключение ложно. Решения представлены ниже.

Аргумент 1:

1. Если животное — собака, то это млекопитающее.
2. Чарли не собака.
3. Следовательно, Чарли не млекопитающее.

Аргумент 2:

1. Все десерты сладкие.
2. Некоторые сладкие продукты содержат мало жира.
3. Итак, все десерты обезжиренные.

Аргумент 3:

1. Если Джад не сделает домашнее задание вовремя, он не пойдет на вечеринку.
2. Джад не идет на вечеринку.
3. Джад не сделал домашнее задание вовремя.

Когда вы закончите работу над тремя аргументами, сравните свои ответы с приведенными ниже решениями.

Решение 1: Недействительно. Если представить, что Чарли — это кошка (или другое животное, которое не является собакой, а является млекопитающим), то обе посылки верны, а вывод — ложен. Чарли — не собака, но Чарли — это млекопитающее.

Решение 2: Недействительно. Торт с масляным кремом — контрпример. Торт с масляным кремом — это десерт, и он сладкий, что показывает, что не все десерты с низким содержанием жира.

Решение3: Недействительно. Предполагая, что первые две посылки верны, вы все равно можете представить, что Джад слишком устал после выполнения домашнего задания и решает не идти на вечеринку, тем самым делая вывод ложным.

Индуктивные выводы

Когда мы рассуждаем индуктивно, мы собираем доказательства, используя наш опыт познания мира, и делаем общие выводы на основе этого опыта. Индуктивное рассуждение (индукция) — это также процесс, посредством которого мы использовать общих убеждений, которые у нас есть о мире, чтобы создать убеждения о нашем конкретном опыте или о том, чего ожидать в будущем. Кто-то может использовать свой прошлый опыт употребления свеклы и абсолютной ненависти к ней, чтобы сделать вывод, что он не любит свеклу любого вида, приготовленную любым способом. Затем они могут использовать этот вывод, чтобы не заказывать салат из свеклы в ресторане, потому что у них есть веские основания полагать, что он им не понравится. Из-за природы опыта и индуктивного вывода этот метод никогда не может гарантировать истинность наших убеждений. В лучшем случае индуктивный вывод дает только вероятные истинные выводы, потому что он выходит за рамки информации, содержащейся в предпосылках. В данном примере прошлый опыт употребления свеклы является конкретной информацией, но человек выходит за рамки этой информации, когда делает общее заявление о том, что ему не нравится вся свекла (даже те сорта, которые он никогда не пробовал, и даже способы приготовления свеклы, которые он никогда не пробовал). ).

Рассмотрим такое убеждение, как «завтра взойдет солнце». Почти три столетия назад шотландский философ Дэвид Юм выступил против достоверности этого убеждения ([1748, 1777] 2011, IV, i). Да, солнце всходило каждое утро в истории человечества (по правде говоря, мы были свидетелями того, что кажется восходом солнца, что является результатом вращения Земли вокруг своей оси и создания феномена дня и ночи). У нас есть наука, чтобы объяснить, почему солнце будет продолжать восходить (поскольку вращение Земли — стабильное явление). Основываясь на современной науке, мы можем обоснованно заключить, что солнце взойдет завтра утром. Но верно ли это предложение ? Чтобы ответить на этот вопрос, вы должны мыслить как философ, что включает в себя критическое осмысление альтернативных возможностей. Скажем, в Землю врезается массивный астероид, который ее уничтожает, или солнце взрывается сверхновой, которая охватывает внутренние планеты и испепеляет их. Эти события крайне маловероятны, хотя в представлении о том, что они могут произойти, не возникает противоречия. Мы верим, что завтра взойдет солнце, и у нас есть веские основания для этой веры, но восход солнца все еще только возможен (даже если он почти неизбежен).

Хотя индуктивные выводы не всегда точны, они все же могут быть вполне надежными. На самом деле многое из того, что мы думаем, что знаем, известно посредством индукции. Более того, хотя дедуктивное рассуждение может гарантировать истинность выводов, если посылки верны, во многих случаях сами посылки дедуктивных аргументов известны индуктивно. Изучая философию, мы должны привыкнуть к возможности того, что наши индуктивно полученные убеждения могут быть ошибочными.

Существует несколько типов индуктивных выводов, но для краткости в этом разделе будут рассмотрены три наиболее распространенных типа: рассуждения от конкретных примеров к общим, рассуждения от общих к конкретным случаям и рассуждения от прошлого к будущему.

Рассуждение от конкретных случаев к общему

Возможно, я сталкиваюсь с несколькими случаями какого-то явления и замечаю, что все экземпляры имеют схожие черты. Например, я заметил, что каждый год примерно во вторую неделю марта краснокрылые дрозды возвращаются оттуда, где они зимовали. Таким образом, я могу сделать вывод, что обычно краснокрылые дрозды возвращаются в район моего проживания (и наблюдаю за ними) во второй декаде марта. Все мои доказательства собраны из частных случаев, но мой вывод носит общий характер. Вот схема:

Экземпляр ₁ , Экземпляр ₂ , Экземпляр ₃ . . . Экземпляр _n —> Обобщение

И поскольку каждый пример служит основанием в поддержку обобщения, примеры являются предпосылками в форме аргумента этого типа индуктивного вывода:

Специально для общей формы индуктивного аргумента:

1. Экземпляр ₁
2. Экземпляр ₂
3. Экземпляр ₃
4. Общий вывод

Рассуждения от общего к конкретным случаям

Индукция может работать и в обратном направлении: рассуждение от общепринятых обобщений к конкретным случаям. Эта особенность индукции основана на том факте, что мы учимся и учимся на прошлом опыте и друг у друга. Многое из того, что мы узнаем, фиксируется в обобщениях. Вы, вероятно, приняли много обобщений от своих родителей, учителей и сверстников. Вы, наверное, считаете, что красный знак «СТОП» на дороге означает, что когда вы едете и видите этот знак, вы должны полностью остановить свой автомобиль. Вы также, вероятно, считаете, что вода замерзает при 32 градусах по Фаренгейту и что курение сигарет вредно для вас. Когда вы используете общепринятые обобщения для предсказания или объяснения вещей в мире, вы используете индукцию. Например, когда вы видите, что ночная минимальная температура прогнозируется на уровне 30°F, вы можете предположить, что вода в вашей ванночке для птиц замерзнет, ​​когда вы встанете утром.

Некоторые мыслительные процессы используют более одного типа индуктивного вывода. Возьмем следующий пример:

Все кошки, которых я когда-либо гладил, не терпят, когда их тянут за хвост.

Так что этот кот, вероятно, не потерпит, чтобы его дергали за хвост.

Обратите внимание, что этот рассудок прошел через ряд экземпляров, чтобы сделать вывод об одном дополнительном экземпляре. Поступая так, рассуждающий неявно предполагал обобщение по пути. Неявное обобщение рассудителя состоит в том, что ни одна кошка не любит, когда ее тянут за хвост. Затем они используют это обобщение, чтобы определить, что сейчас им не следует тянуть кошку перед собой за хвост. Рассуждающий может использовать несколько примеров из своего опыта в качестве посылок, чтобы сделать общий вывод, а затем использовать это обобщение в качестве предпосылки, чтобы сделать вывод о конкретном новом случае.

Индуктивное рассуждение находит отражение в повседневных выражениях, таких как «Где дым, там и огонь». Когда люди видят дым, они интуитивно верят, что есть огонь. Это результат индуктивного рассуждения. Подумайте о своем собственном мыслительном процессе, изучая рисунок 5.5.

Рисунок 5,5 «Где дым, там и огонь» — пример индуктивного рассуждения. (кредит: «20140803-FS-UNK-0017» Министерства сельского хозяйства США/Flickr, CC BY 2.0)

Рассуждение от прошлого к будущему

Мы часто используем индуктивные рассуждения, чтобы предсказать, что произойдет в будущем. Основываясь на нашем богатом опыте прошлого, у нас есть основа для предсказаний. Рассуждение от прошлого к будущему подобно рассуждению от конкретных случаев к общему. У нас есть опыт событий во времени, мы замечаем закономерности, касающиеся возникновения этих событий в определенное время, а затем делаем вывод, что событие произойдет снова в будущем. Например:

Каждое утро я вижу, как моя соседка выгуливает собаку. Так что моя соседка, вероятно, сегодня утром выгуляет свою собаку.

Может ли рассуждающий таким образом человек ошибаться? Да, сосед может быть болен, или собака может быть у ветеринара. Но в зависимости от регулярности утренних прогулок с собакой и количества таких случаев (скажем, сосед выгуливал собаку каждое утро в течение последнего года), вывод может быть верным, несмотря на то, что это возможно. неправильный.

Сильные индуктивные выводы

Сила индуктивных выводов зависит от надежности посылок, данных в качестве доказательства, и их отношения к сделанным выводам. сильный индуктивный вывод — это вывод, в котором, если предлагаемые доказательства верны, то вывод, вероятно, верен. слабый индуктивный вывод — это вывод, при котором, если предлагаемые доказательства верны, вывод, вероятно, не верен. Но насколько сильным должен быть вывод, чтобы считаться хорошим, зависит от контекста. Слово «вероятно» расплывчато. Если что-то более вероятно, чем нет, то это должно произойти как минимум с вероятностью 51 %. Однако в большинстве случаев мы ожидали бы иметь гораздо более высокую планку вероятности, чтобы считать вывод сильным. В качестве примера этой зависимости от контекста сравните вероятность, считающуюся высокой в ​​азартных играх, с гораздо более высокой вероятностью точности, которую мы ожидаем при определении вины в суде.

На рис. 5.6 показаны три формы рассуждений, используемых в научном методе. Индукция используется для сбора закономерностей и обобщений, на основе которых строятся гипотезы. Гипотезы проверяются, и если они остаются не опровергнутыми, снова используется индукция, чтобы предположить поддержку гипотезы.

Рисунок 5. 6 Введение в научный метод (атрибуция: Copyright Rice University, OpenStax, лицензия CC BY 4.0)

Абдуктивное рассуждение

Абдуктивное рассуждение похоже на индуктивное рассуждение тем, что обе формы вывода являются вероятностными. Однако они различаются отношением посылок к заключению. В индуктивной аргументации доказательства в посылках используются для обоснования вывода. В абдуктивных рассуждениях заключение предназначено для объяснения доказательств, предлагаемых в посылках. При индукции посылки объясняют заключение, а при абдукции заключение объясняет посылки.

Вывод наилучшего объяснения

Поскольку похищение происходит от улик к наиболее вероятному объяснению этих улик, его часто называют «выводом к наилучшему объяснению». Мы начинаем с набора данных и пытаемся придумать какую-нибудь объединяющую гипотезу, которая могла бы наилучшим образом объяснить существование этих данных. Учитывая эту структуру, доказательства, которые необходимо объяснить, обычно принимаются как истинные всеми вовлеченными сторонами. В центре внимания находится не истинность доказательств, а то, что они означают.

Хотя вы можете и не осознавать, вы регулярно используете эту форму рассуждений. Допустим, ваша машина не заводится, а двигатель даже не заводится. Кроме того, вы замечаете, что индикаторы радио и дисплея не горят, даже когда ключ вставлен и повернут в положение ON. Учитывая это свидетельство, вы заключаете, что лучшее объяснение состоит в том, что есть проблема с батареей (либо она не подключена, либо разряжена). Или, возможно, вы испекли тыквенный хлеб утром, но его нет на прилавке, где вы его оставили, когда пришли домой. На полу крошки, и мешок, в котором он был, тоже на полу, порванный в клочья. У вас есть собака, которая была дома весь день. Рассматриваемая собака лежит на диване, низко опустив голову, прижав уши назад, избегая зрительного контакта. Учитывая улики, вы заключаете, что лучшее объяснение пропажи хлеба состоит в том, что его съела собака.

Детективы и судебные следователи используют похищение, чтобы придумать лучшее объяснение того, как и кем было совершено преступление. Эта форма рассуждений также незаменима для ученых, которые используют наблюдения (доказательства) наряду с принятыми гипотезами для создания новых гипотез для проверки. Вы также можете распознать похищение как форму рассуждения, используемую в медицинских диагнозах. Врач рассматривает все ваши симптомы и любые дополнительные доказательства, полученные от предварительных анализов и причин, до наилучшего возможного заключения (диагноза) о вашем заболевании.

Объяснительные качества

Хорошие абдуктивные умозаключения имеют некоторые общие черты. Объяснительные достоинства — это аспекты объяснения, которые обычно делают его сильным. Есть много объяснительных достоинств, но мы сосредоточимся на четырех. Хорошая гипотеза должна быть объяснительной, простой и консервативной и должна иметь глубину .

Сказать, что гипотеза должна быть объяснительной просто означает, что она должна объяснять все имеющиеся данные. Слово «объяснительный» для наших целей используется в более узком смысле, чем в повседневном языке. Возьмем пример с тыквенным хлебом: человек может подумать, что его сосед по комнате съел буханку тыквенного хлеба. Однако такое объяснение не объясняло ни того, почему крошки и мешок оказались на полу, ни виноватой позы собаки. Обычно люди не съедают целую буханку тыквенного хлеба, а если и съедают, то не выпотрошат пакет при этом, а даже если бы и съели, то, вероятно, спрятали бы улики. Таким образом, объяснение, что ваш сосед по комнате съел хлеб, не так объяснительно, как то, которое указывает на вашу собаку как на виновника.

Но что, если вы решите, что другая собака зашла в дом и съела хлеб, а затем снова вышла, и ваша собака выглядит виноватой, потому что она ничего не сделала, чтобы остановить незваного гостя? Это объяснение, кажется, объясняет пропажу хлеба, но оно не так хорошо, как более простое объяснение, что преступником является ваша собака. Часто хорошим объяснением является простое . Возможно, вы слышали о бритве Оккама , сформулированной Уильямом Оккамом (1287–1347), которая гласит, что самое простое объяснение — лучшее объяснение. Оккам говорил, что «сущности не следует умножать сверх необходимости» (Spade & Panaccio 2019).). Под «сущностями» Оккам имел в виду понятия, механизмы или движущиеся части.

Примеров непростых объяснений предостаточно. Например, теории заговора представляют собой полную противоположность простоте, поскольку такие объяснения сложны по самой своей природе. Теории заговора должны постулировать заговоры, закулисные сделки, сокрытия (чтобы объяснить существование альтернативных доказательств) и маниакальных людей, чтобы объяснить явления и далее объяснить более простое объяснение этих явлений. Теории заговора никогда не бывают простыми, но это не единственная причина, по которой они вызывают подозрения. Теории заговора также, как правило, лишены достоинства быть консервативный и имеющий глубину .

консервативное объяснение поддерживает или сохраняет большую часть того, во что мы уже верим. Консервативность в науке — это когда теория или гипотеза согласуется с другими устоявшимися научными теориями и объяснениями. Например, теория, которая объясняет какое-то физическое явление, но при этом не нарушает первый закон движения Ньютона, является примером консервативной теории. С другой стороны, рассмотрим теорию заговора о том, что мы никогда не высаживались на Луну. Кто-то может предположить, что транслируемая по телевидению посадка Аполлона-11 была снята где-то в секретной студии. Но реальность первой показанной по телевидению высадки на Луну — не единственное убеждение, от которого мы должны избавиться, чтобы поддержать теорию. Произошло еще пять пилотируемых посадок на Луну. Кроме того, реальность высадок на Луну согласуется с представлениями о технологическом прогрессе в течение следующих пяти десятилетий. Многие из разработанных технологий позже были приняты военным и частным сектором (NASA, n.d.). Более того, миссии «Аполлон» являются ключевым фактором в понимании космической гонки эпохи холодной войны. Принятие теории заговора требует отказа от широкого круга убеждений, поэтому эта теория не является консервативной.

Теоретик заговора может предложить альтернативные объяснения, чтобы объяснить противоречие между их объяснением и устоявшимися убеждениями. Однако каждое объяснение, предлагаемое заговорщиком, вызывает все больше вопросов. И хорошее объяснение не должно вызывать больше вопросов, чем дает ответов. Эта характеристика является достоинством глубины . Глубокое объяснение избегает необъяснимых объяснителей, или объяснения, которое само нуждается в объяснении. Например, теоретик может заявить, что Джону Гленну и другим астронавтам промыли мозги, чтобы объяснить рассказы астронавтов из первых рук. Но это утверждение поднимает вопрос о том, как работает «промывание мозгов». Кроме того, как насчет учетных записей тысяч других сотрудников, работавших над проектом? Им всем промыли мозги? И если да, то как? Объяснение конспиролога вызывает больше вопросов, чем дает ответов.

Чрезвычайные претензии требуют экстраординарных доказательств

Возможно ли, что наши устоявшиеся убеждения (или научные теории) могут быть ошибочными? Зачем отдавать предпочтение объяснению, потому что оно поддерживает наши убеждения? Научная мысль никогда бы не продвинулась вперед, если бы мы все время полагались на консервативные объяснения. На самом деле объяснительные добродетели — это не законы, а эмпирические правила, ни одно из которых не является высшим или необходимым. Иногда правильное объяснение более сложное, а иногда правильное объяснение требует, чтобы мы отказались от давних убеждений. Новые и революционные объяснения могут быть сильными, если у них есть доказательства, подтверждающие их. В науках этот подход выражается в следующем принципе: Чрезвычайные претензии потребуют экстраординарных доказательств. Другими словами, новому утверждению, которое противоречит общепринятым знаниям, потребуется больше доказательств, чтобы сделать его достоверным, чем утверждению, которое уже согласуется с общепринятыми знаниями.

Таблица 5.2 суммирует только что рассмотренные три типа выводов.

Тип вывода	Описание	Соображения
Дедуктивный	Фокусируется на структуре аргументов	Обеспечивает достоверные выводы, когда его структура гарантирует истинность его вывода	Делает неверные выводы, когда, даже если посылки верны, вывод может быть ложным
Индуктивный	Использует общие представления о мире для создания убеждений о конкретном опыте или для предсказания будущего опыта	Сильный, если вывод, вероятно, верен при условии, что доказательства верны	Слабо, если вывод, вероятно, неверен, даже если предлагаемые доказательства верны
Похищение	Объяснение предлагается для обоснования и объяснения показаний	Сильный, если объяснительный, простой, консервативный и глубокий	Чрезвычайные заявления требуют экстраординарных доказательств

Стол 5. 2 Три типа умозаключений

логических выводов | Разоблачение науки

Введение

Рисунок 1. Вывод

Мы делаем выводы так же часто, как чистим зубы. Каждый день, часто неосознанно, мы делаем выводы на основе поведения самих себя и других, нашего окружения и нашего взаимодействия с окружающими нас людьми. Существует два типа умозаключений: индуктивный и дедуктивный. Индуктивные выводы начинаются с наблюдения и расширяются до общего вывода или теории. Например, если чья-то собака входит внутрь в День поминовения, когда начинается фейерверк, а затем снова входит внутрь 4 июля, когда начинаются фейерверки, но остается снаружи в течение всего барбекю в день вашего рождения без фейерверков, а затем входит внутрь на Новый год. Накануне во время фейерверка можно сделать вывод, что его собака боится фейерверков. Дедуктивные выводы противоположны. Процесс дедуктивного вывода начинается с общей теории, а затем оттачивается на конкретном наблюдении или подтверждении. Например, если кто-то знает, что фейерверки не могут запускаться под дождем, то он или она может сделать дедуктивный вывод и прийти к выводу, что если идет дождь, фейерверки будут отменены. Научный метод применяется к выводу посредством шагов, предпринимаемых для получения как индуктивных, так и дедуктивных выводов. Индуктивный вывод начинается с наблюдения, а затем развивается модель такого наблюдения. Затем делается гипотеза, основанная на образце, и, наконец, теория, основанная на гипотезе. Дедуктивное рассуждение начинается с широкой теории, затем формулируется гипотеза, и из этой гипотезы могут быть сделаны наблюдения, которые помогают прийти к заключению и подтвердить исходную теорию. Однако проблемы возникают, когда нет достаточного количества статистических данных для поддержки выводов ученых, потому что общественность часто считает определенные исследования и выводы ученых верными без надлежащих статистических данных. Общественность очень доверяет ученым, врачам и образованным специалистам, иногда не проверяя необходимые факты. Статистический вывод — это вывод, сделанный при наличии неопределенности, а ошибка — это неверный вывод. Ученые часто делают выводы на основе предположений, сделанных в отношении небольшого населения, а затем утверждают, что такие предположения репрезентативны и применимы ко всему населению. В этой главе мы обнаружим различные типы выводов на примерах и дополнительно оценим упомянутые неправильные представления о выводах, которые затрагивают как общественность, так и ученых.

Неправильные представления о выводах

Согласно Statistically Significant Consulting , статистический вывод «основан на математических законах вероятности». С помощью статистического вывода мы можем сформулировать гипотезу и использовать математику и вероятность, чтобы проверить, насколько верна наша гипотеза для выборочной совокупности. Значение p — это значение, используемое для определения точности данных выборки, даже если нулевая гипотеза эксперимента верна. Даже если мы не уверены в точных числах или вероятностях, мы можем сделать вывод, предоставляют ли наши данные убедительные доказательства в пользу нашей нулевой гипотезы или против нее. Редко кто-то знает форму или стандартное отклонение определенных данных, и возможность вернуться назад, чтобы получить наши собственные данные для определенного эксперимента, не является вариантом. Мы должны часто оценивать данные, не зная формы или стандартного отклонения совокупности. «Стандартные статистические тесты требуют предположений». Мы должны понимать, что точность и «достоверность наших данных» зависят от наших предположений. Статистический вывод можно описать как цепочку предположений и рассуждений. Распространенная ошибка возникает, когда кто-то путается в определении причины определенного аспекта цепочки. Большинство людей забывают, что выборочное распределение — это всего лишь распределение выборочных данных. Каждая часть данных представляет собой среднее значение одной выборки из предложенной совокупности. Распределение выборки никоим образом не является репрезентативным для всех или всего. Еще одно распространенное заблуждение состоит в том, что по мере роста размера выборки определенного эксперимента полученные данные должны становиться более похожими на данные генеральной совокупности. Больший размер выборки автоматически не приводит к более точному представлению выборочной совокупности.

Дедуктивное и индуктивное мышление часто путают друг с другом.

Рисунок 2. Логика

обоснованных рассуждений. Когда мы начинаем с большой мысли, идеи, гипотезы или концепции и приходим к конкретному подробному заключению посредством рассуждений, мы используем дедуктивный вывод. Ученые использовали дедуктивное рассуждение с научным методом, когда пытались проверить гипотезу или теорию. Часто люди выдвигают неверные гипотезы, что приводит к ошибочности их дедуктивного вывода. Чтобы дедуктивные выводы были верными, гипотеза или общая идея должны быть верными. Если что-то верно для подавляющего большинства или класса людей, то это верно и для каждого отдельного человека в большинстве или классе. Например: «Все растения — живые организмы. Папоротник — это растение». Следовательно, «Папоротник — это живой организм» верно. Поскольку две посылки «Все растения — живые организмы» и «Папоротник — это растение» верны, вывод «Папоротник — это живой организм» также верен. Проблема с дедуктивными выводами заключается в том, что можно прийти к логическому и общему заключению, даже если посылки ложны. Например: «Все бабушки пекут печенье и горячий шоколад. Мария — бабушка. Следовательно, Мэри печет печенье и горячий шоколад», — логичный вывод, однако он не соответствует действительности, поскольку первая посылка «Все бабушки пекут печенье и горячий шоколад» неверна. Легко совершить ошибку, приняв вывод за истину, даже если первая посылка ложна из-за стереотипов или общепринятых культурных идей. Часто в сказках или фильмах бабушки пекут теплое печенье и горячий шоколад для своих внуков, поэтому ребенок может поверить в то, что вывод «все бабушки пекут печенье и горячий шоколад» верен, однако зрелый взрослый или подросток может отличить вымысел от реальности. В науке посылки и выводы не всегда так легко определить, являются ли они истинными или ложными, что может заставить человека поверить в правильность определенного вывода, сделанного с помощью дедуктивных рассуждений, из-за путаницы или просто из-за недостатка образования.

Силлогизм — это форма дедуктивного рассуждения. В силлогизме есть две посылки: большая и меньшая. У основных и второстепенных посылок есть общая мысль или идея, которая связывает их и формирует логический вывод. Например, за фразой «Каждый график показывает положительный рост» следует предпосылка «Данные за 2011 год организованы в один из графиков». Обе эти предпосылки приводят к выводу: «Данные за 2011 год показывают положительный рост». Силлогизм часто используется для проверки обоснованности определенного аргумента.

Индуктивный вывод, с другой стороны, формирует общие выводы или обобщения, основанные на небольших конкретных наблюдениях. Паттерны формируются в рамках определенных наблюдений, что позволяет людям формировать обобщения, а затем выводить теорию. Индуктивный вывод трудно освоить, потому что обе посылки определенного вывода могут быть истинными и все равно приводить к ложному заключению. Например, «Кэти — студентка. У Кати учебный период. Поэтому у всех студентов есть периоды обучения». Вывод не только неверен, но и логически не следует двум посылкам. В науке может быть трудно распознать ложный вывод, если обе посылки верны, что часто бывает в индуктивных выводах. Вассертхейл-Смоллер сказал Live Science: «В науке происходит постоянное взаимодействие между индуктивным выводом (основанным на наблюдениях) и дедуктивным выводом (основанным на теории), пока мы не станем все ближе и ближе к «истине», к которой мы можем только приближаться, но не можем. установить с полной уверенностью».

Рисунок 3. Аргумент

Третий тип вывода, о котором меньше говорят, — абдуктивный вывод. Согласно Brute College, абдуктивный вывод «обычно начинается с неполного набора наблюдений и переходит к наиболее вероятному из возможных объяснений для группы наблюдений». Люди должны выдвигать гипотезы на основе предоставленной им информации. Если информация неверна или расплывчата, гипотеза будет неверной. Абдуктивные умозаключения, по сути, являются результатом обоснованных догадок. Врачи часто делают абдуктивные выводы после того, как выслушают симптомы пациента, чтобы диагностировать конкретное заболевание или травму. Абдуктивный вывод также используется в системе правосудия, когда присяжные выслушивают доводы обеих сторон по делу, чтобы сделать вывод, считают ли они человека виновным или невиновным. Понятно, почему абдуктивный вывод может заставить людей сделать неверный вывод. Люди только оценивают определенные моменты и делают вывод, основанный исключительно на том, как они интерпретируют эти моменты. Один человек может прийти к совершенно другому выводу, чем другой человек, посредством абдуктивного вывода после того, как они оба рассмотрели одни и те же наблюдения. Личный опыт, религиозные убеждения, политические взгляды и культурные различия могут влиять на выводы, сделанные каждым человеком.

Как избежать ошибок с помощью выводов

            Марко Мароцци рассматривает неправильное использование статистики в связи с выводами в . Плохое умозаключение вытесняет хорошее? В частности, в области медицины Мароцци заявляет, что во избежание определенных статистических ошибок в медицинских журналах каждый журнал должен иметь своих собственных статистиков для проверки информации перед ее публикацией. Кто-то совершает ошибку, когда занимает позицию или пытается убедить кого-то другого занять позицию, основанную на неверной предпосылке. Многочисленные источники указывают на важность базового критического мышления при попытке избежать ошибки.

Заключение

В заключение, индуктивные выводы имеют место, когда наблюдения за конкретными случаями приводят к выводам из более общих идей, а дедуктивные выводы возникают, когда факты общих принципов приводят к выводам о частных случаях посредством логических правил. Человеку легко сделать неверный вывод, если он недостаточно образован или не уверен в достоверности предпосылок каждого вывода. Надлежащие методы критического мышления и уверенность в том, что собранные данные верны, могут помочь удержать людей от неверных выводов на основе умозаключений.

 

Ссылки

Брэдфорд, Алина (2015, 23 марта). Дедуктивное рассуждение против индуктивного рассуждения. Получено

Из http://www.