Уровни абстракций — ключ к пониманию архитектурных изысков ПО
Эта статья будет в большей степени полезна новичкам, только начинающим работать с абстракциями и построением архитектур ПО. Однако искренне надеюсь, что и более опытные специалисты смогут найти для себя что-то интересное в этом материале.
Абстракция — один из набивших оскомину столпов ООП. В любом курсе по программированию с вероятностью 99% можно найти урок-другой, посвященный теме абстракции. И практически всегда упускается более широкое, всеобъемлющее понятие «уровней абстракции» — на мой взгляд, критически важное, ключевое для понимания всех остальных принципов проектирования.
Модель объекта и ступень приближения
Абстракция — это модель некоего объекта или явления реального мира, откидывающая незначительные детали, не играющие существенной роли в данном приближении. И уровень абстракции — это и есть наша ступень приближения. Каждый человек способен строить абстракции — это отличительная способность homo sapiens.
Чтобы не вдаваться в многоэтажную теорию, приведу наглядный пример. Итак, раскладываем по полочкам. Представьте себе, что вы решили испечь яблочный пирог. Вы берете толстую кулинарную книгу с полки (для любителей, все остальные — в сеть), открываете нужный вам рецепт и читаете нечто следующее:
«Чтобы испечь яблочный пирог, нам понадобится два килограмма непременно свежих яблок, румяных, как девичьи щёки на крещенском морозе. Помнится, видал я такие щёчки у моей ненаглядной Лизоньки, когда мы впервые с ней встретились, и она угощала меня яблочными пирогами, состряпанными на последние деньги, которые она выручила от продажи дедовских коллекционных монет 1819 года, выпущенных при императоре таком-то…» И т.д, и т.п.
Если вы осилили текст курсивом, то вы очевидно заметили, что он имеет весьма посредственное отношение к тому, что нам нужно. Собственно, к тому, как же печь эти чертовы пироги из яблок, не правда ли?
А теперь вспомните, как часто в коде нам приходится встречать логические конструкции типа if-if-if-else-if-else-if, содержащие тонны вложенных рассуждений. Приходится читать все эти адские нагромождения и держать в голове всю цепочку событий, для того, чтобы понять, что тут вообще происходит и какое отношение «вот это всё» имеет к заявленному содержанию (название класса/функции по аналогии с названием рецепта «яблочный пирог»).
Приходится читать все эти адские нагромождения и держать в голове всю цепочку событий, для того, чтобы понять, что тут вообще происходит и какое отношение «вот это всё» имеет к заявленному содержанию (название класса/функции по аналогии с названием рецепта «яблочный пирог»).
А ведь что на самом деле нас интересовало в рецепте? Нам нужно было знать, сколько и каких продуктов нам понадобится и что затем с ними делать. Нас абсолютно не интересует в этом приближении (на данном уровне абстракции), каким образом эти продукты к нам попали (более низкие уровни абстракции) и что мы будем делать с этим пирогом потом (более высокие уровни абстракции). Это очевидно. Но тысячи программистов продолжают игнорировать эти принципы и пишут мозговыносные структуры if-if-else-if…
А бывает так, что в рецепте встречаются умные словечки типа «бланшировать» или «сделать бизе». В хороших кулинарных руководствах описание подобных практик выносят в отдельные главы, а в самих рецептах лишь ссылаются на страницы с подробным описанием техники (привет, Инкапсуляция).
Построение структуры
Конечно, бывают и обратные ситуации, когда за тоннами слоёв абстракций невозможно уловить нить повествования. Но в этом-то и состоит мастерство архитектора ПО — спроектировать достаточно простую для сопровождения, то есть понимания, структуру. «Не нужно быть умным — нужно быть понятным» ©.
В то же время, не терять в эффективности решения бизнес-задач. В некоторой мере, это искусство. Каждый конкретный архитектор (программист) будет рисовать эту картину, то есть создавать модель мира по-своему: «Я художник — я так вижу». Вот вам пища в топку холиваров на счет единых стандартов программирования в рамках команды и необходимости наличия исполнителя роли архитектора.
Абстракция и Реализация
Есть ещё один момент, о котором я хочу упомянуть: путешествие между слоями логик. Красиво изолированный уровень абстракции достаточно прост для понимания: у нас есть ряд объектов, очевидным образом взаимодействующих между собой, уровни вложенности маленькие (если они вообще есть — как в рецепте пирога). Однако, как нам уже стало понятно, самым трудозатратным для понимания является перемещение между уровнями абстракций.
Однако, как нам уже стало понятно, самым трудозатратным для понимания является перемещение между уровнями абстракций.
Чтобы упростить этот процесс, стоит разобраться в природе дуальности понятий Абстракции и Реализации. В этом моменте обычно и фокусируются на различных курсах по программированию, перед этим упуская понятие уровня абстракции. Из-за чего у студентов формируется заблуждение, что ООП — это что-то запредельно сложное.
Возьмем для примера такую цепочку слоёв абстракций: нам нужен пирог для Дня рождения друга. Спускаемся ниже: пирог может быть фруктовый или мясной. А может, рыбный? В момент рассуждений о том, что нам нужен какой-то пирог в качестве подарка, он (пирог) выступает конечным элементом данного уровня абстракции. В этот момент пирог — это реализация подарка (но он может быть любой: бритва, деньги, конструктор лего — это всё варианты подарка). Когда мы совершаем переход на более низкий уровень абстракции, наш объект (пирог) превращается из конечной реализации в абстракцию: уже нас не устраивает уровень детализации «какой-то пирог», мы начинаем искать его реализацию (привет, Полиморфизм).
Таким образом, считать объект абстрактным или реальным — зависит исключительно от степени детализации моделируемого «мира» и от бизнес-задач, поставленных перед архитектором. И, разумеется, от его чувства прекрасного.
С моей точки зрения, понимая явление уровней абстракций, можно легко разобраться во всех принципах и шаблонах проектирования.
P.S. Написать эту статью меня побудило энное предложение стать лектором на очередных курсах по программированию. И, хотя, у меня и есть желание испытать подобный опыт, в данный период моей жизни и в обозримом будущем это не представляется возможным. Я решила, что моё желание рассказывать о сложных вещах простым и понятным образом (надеюсь, это так) пусть лучше выльется в какое-то количество статей, нежели будет погребено под тоннами лет бездействия.
Если моя манера изъясняться была кому-то полезной в достижении состояния «дзен» и вообще «пишите, Шура», то в будущем, вероятно, напишу «о чём-то таком ещё».
Продолжение
Все про українське ІТ в Телеграмі — підписуйтеся на канал редакції DOU
Теми: ООП, ООП — это просто, програмування
Причуды абстракций / Хабр
За годы преподавания и коммерческой разработки я повстречал много студентов и разработчиков, которые не до конца понимают смысл слова абстракция. Из многочисленных попыток разъяснить смысл этого термина получилась настоящая статья. Что Вы найдете под катом:
- Определение понятия абстракции и объяснение откуда оно взялось в ООП.
- Объяснение на простых примерах, что такое барьер абстракции, побочный эффект абстракции.
- Как получается хардкод.
Что такое абстракция?
Википедия определяет абстракцию и процесс абстрагирования следующим образом:
Абстра́кция (от лат. abstractio — отвлечение) — отвлечение в процессе познания от несущественных сторон, свойств, связей объекта (предмета или явления) с целью выделения их существенных, закономерных признаков; абстрагирование; теоретическое обобщение как результат такого отвлечения.
В европейской философии и логике абстрагирование трактуется как способ поэтапного продуцирования понятий, которые образуют всё более общие модели — иерархию абстракций. Наиболее развитой системой абстракций обладает математика. Степень отвлечённости обсуждаемого понятия называется уровнем абстракции. В зависимости от целей и задач, можно рассуждать об одном и том же объекте на разных уровнях абстракции.
Гради Буч определяет понятие абстракции значительно проще, но смысл тот же:
Абстракция выделяет существенные характеристики некоторого объекта, отличающие его от всех других объектов.
Зачем нужна абстракция?
Абстракции выполняют защитную функцию и помогают нам не сойти с ума от переизбытка информации. Представьте, как бы нам жилось, если при письме шариковой ручкой пришлось бы думать о том, что миллиарды молекул чернил взаимодействуют с молекулами бумаги, чтобы получилась буква. Другими словами, не тратя время на ненужные подробности, мы можем ухватить самую суть — взглянуть на проблему «сверху».
Если бы не фотография с высоты птичьего полета, можно ли было бы себе представить насколько правильно спроектирована Барселона? Кстати, про пример с шариковой ручкой, читать бы тоже не получилось — начертания одной и той же буквы на письме отличаются даже у одного человека.
Абстрактное мышление — это механизм, который позволяет нам перерабатывать и усваивать кучу новых сведений. Если бы не было абстракции, то единственный вариант для нас — это остаться очень примитивными существами.
В Бразилии живет племя небольшое племя индейцев Пираха. Представители этой народности обладают крайне скудным абстрактным мышлением. Их алфавит состоит из трех гласных и восьми согласных. У них нет слов, обозначающих цифры, вместо цифр у них два понятия — несколько и много. У них нет цветов — только понятия светлый и темный, времени и истории — они живут только сегодняшним днем и помнят только то. что помнит старейший из ныне живущих; нет — религии, ремесел, искусства. У них еще много чего нет в нашем привычном понимании.
Итак, абстрагирование нам нужно как способ познания и описания окружающего мира, для обмена информацией друг с другом. Абстракции позволяют провести декомпозицию предметной области на набор понятий и связей между ними.
На картинке изображен Legoland в Лондоне. Несмотря на то, что все предметы собраны из детского конструктора, мы без труда узнаем в них дома, окна, двери, городские кварталы, людей.
Барьеры и побочные эффекты абстракций
Чтобы понять ключевые свойства абстракций проведем аналогию с построением проекций на плоскость.
Предположим, что у нас есть три фигуры: шар, цилиндр и параллелепипед, при этом ось симметрии цилиндра, проходящая через центры окружностей в основании, параллельна какой-нибудь оси симметрии параллелепипеда. Очевидно, что можно выбрать две плоскости для построения проекций таким образом, что шар и цилиндр спроецируются в окружности, а цилиндр и параллелепипед — в прямоугольники.

Проекция в нашем примере иллюстрирует абстракцию объекта — геометрической фигуры. Что мы видим — на одной плоскости не отличишь проекции шара и цилиндра, а на другой — цилиндра и параллелепипеда. Этот эффект называется барьером абстракции. Абстракция представляет не весь объект целиком, а только лишь его существенный набор характеристик.Нужно быть готовым к тому, что некоторые очень непохожие друг на друга объекты, могут стать неразличимыми. Если это неудобно, то нужно выбирать другой набор абстракций.
С другой стороны, как мы видим из примера, цилиндр, может проецироваться и в окружность, и в прямоугольник — объекты с различными геометрическими свойствами, отличными от тех, что есть у цилиндра. Наличие у абстракции собственных свойств, отличных от свойств абстрагируемого объекта, называется побочным эффектом абстракции.
На самой первой картинке изображены две фигуры, собранные из щепок, так что при определенном освещении они отбрасывают «человеческие тени».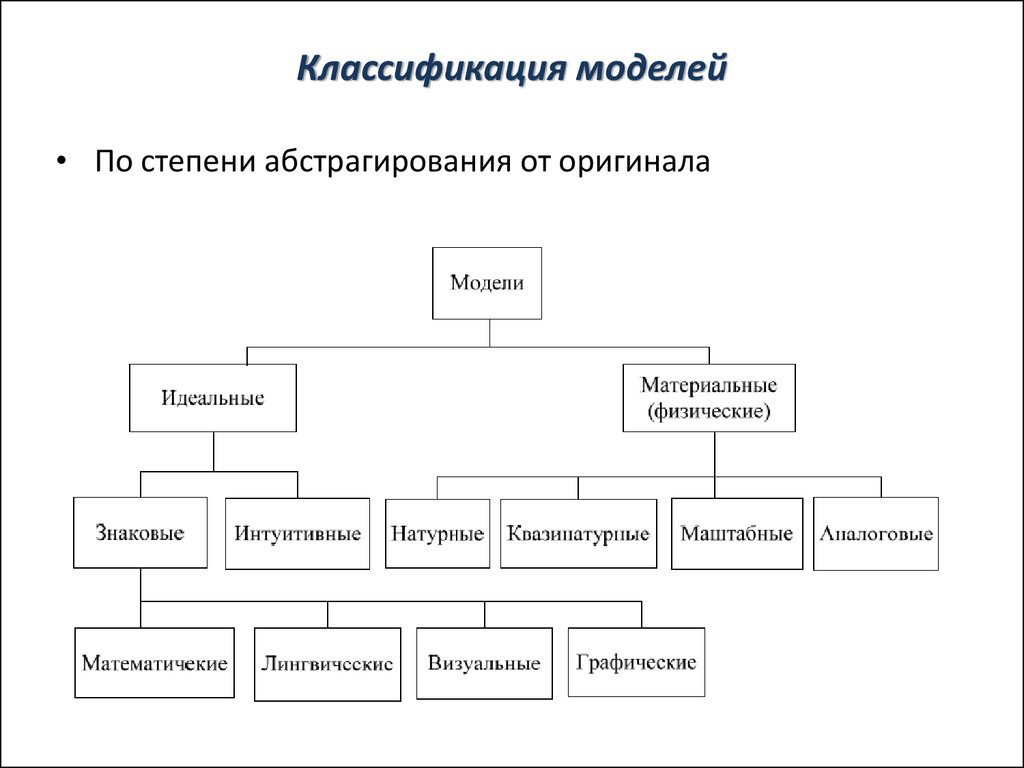 разрядность (8, 16, 32, 64 бита)
Данная абстракция позволяет представить целые числа только из отрезка –p/2+1 до p/2. Побочный эффект – проблема переполнения.
Вещественные числа
Числа с плавающей точкой
Вещественных чисел несчетное число, а чисел с плавающей точкой — всего лишь конечное. Это значит, что несчетное количество вещественных чисел представлены одним числом с плавающей точкой. Побочный эффект – ошибка округления, из-за который два числа нельзя сравнивать с помощью операции сравнения, а лишь по модулю некоторого маленького epsilon |a-b| < epsilon => a == b, или a/b*1000 может сильно отличаться от a*1000/b. Появилась даже целая дисциплина в математике – численные методы, которая изучает как организовать вычисления с плавающей точкой так, чтобы результаты не сильно отличались от вычислений с вещественными числами.
Деньги
Числа с плавающей точкой
Погрешность округления чисел с плавающей точкой делает, если не невозможным их использование для финансовых операций, то, по крайней мере, сильно усложняет жизнь.
разрядность (8, 16, 32, 64 бита)
Данная абстракция позволяет представить целые числа только из отрезка –p/2+1 до p/2. Побочный эффект – проблема переполнения.
Вещественные числа
Числа с плавающей точкой
Вещественных чисел несчетное число, а чисел с плавающей точкой — всего лишь конечное. Это значит, что несчетное количество вещественных чисел представлены одним числом с плавающей точкой. Побочный эффект – ошибка округления, из-за который два числа нельзя сравнивать с помощью операции сравнения, а лишь по модулю некоторого маленького epsilon |a-b| < epsilon => a == b, или a/b*1000 может сильно отличаться от a*1000/b. Появилась даже целая дисциплина в математике – численные методы, которая изучает как организовать вычисления с плавающей точкой так, чтобы результаты не сильно отличались от вычислений с вещественными числами.
Деньги
Числа с плавающей точкой
Погрешность округления чисел с плавающей точкой делает, если не невозможным их использование для финансовых операций, то, по крайней мере, сильно усложняет жизнь.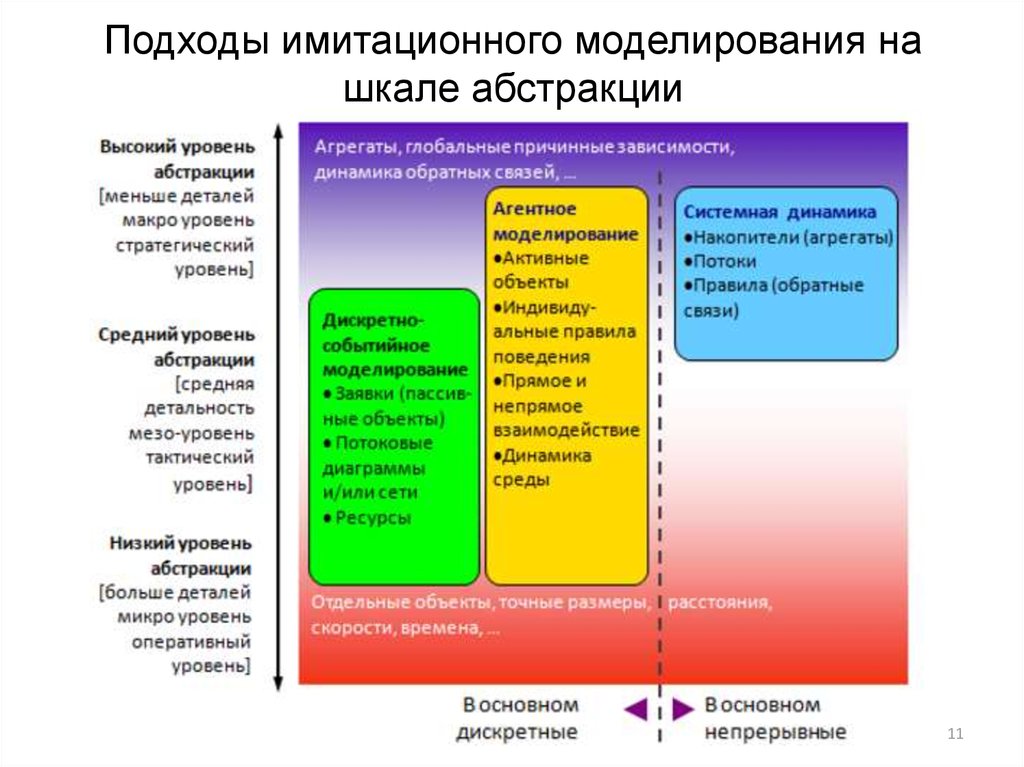 В любом случае, я бы сначала подумал в сторону написания отдельного класса для денежных единиц.
Изображение
Машинная графика
Машинная графика развивается семимильными шагами, чтобы сделать изображение на экране компьютера все более реалистичным.
Программное обеспечение
Процедура
Процедура является базовым элементом декомпозиции в процедурном программировании. Побочный эффект — процедура жестко заданная последовательность команд, которую невозможно изменить без переписывания самой процедуры.
Программное обеспечение
Класс
О классах будем говорить ниже.
Предметная область
Абстракция сущности и связи между сущностями
Побочный эффект — отражает представление, заблуждения, предубеждения и т.д. о предметной области конкретного субъекта.
Бизнес-логика
Процедура
Как уже говорилось выше — побочный эффект процедуры — жесткая последовательность команд.
В любом случае, я бы сначала подумал в сторону написания отдельного класса для денежных единиц.
Изображение
Машинная графика
Машинная графика развивается семимильными шагами, чтобы сделать изображение на экране компьютера все более реалистичным.
Программное обеспечение
Процедура
Процедура является базовым элементом декомпозиции в процедурном программировании. Побочный эффект — процедура жестко заданная последовательность команд, которую невозможно изменить без переписывания самой процедуры.
Программное обеспечение
Класс
О классах будем говорить ниже.
Предметная область
Абстракция сущности и связи между сущностями
Побочный эффект — отражает представление, заблуждения, предубеждения и т.д. о предметной области конкретного субъекта.
Бизнес-логика
Процедура
Как уже говорилось выше — побочный эффект процедуры — жесткая последовательность команд.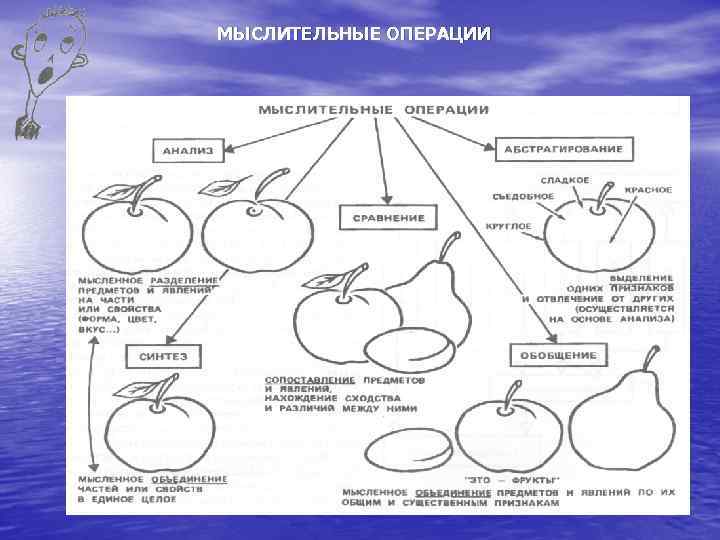 Бизнес-логика же подвержена изменениям, как правило содержит много исключений, о которых пользователи обычно забывают рассказать. Попытка представить бизнес-операцию в виде процедуры часто делает терпит неудачу.
Программное обеспечение
Поток для распараллеливания операций
Многопоточное программирование получилось настолько сложным для восприятия, что немного людей в нем разбирается.
Квадрат — это прямоугольник, у которого все стороны равны.
Класс квадрат нельзя наследовать от прямоугольника.
Классы — это абстракции. У них есть свои собственные свойства, которые отличаются от математических объектов и которые делают невозможным наследование.
Бизнес-логика же подвержена изменениям, как правило содержит много исключений, о которых пользователи обычно забывают рассказать. Попытка представить бизнес-операцию в виде процедуры часто делает терпит неудачу.
Программное обеспечение
Поток для распараллеливания операций
Многопоточное программирование получилось настолько сложным для восприятия, что немного людей в нем разбирается.
Квадрат — это прямоугольник, у которого все стороны равны.
Класс квадрат нельзя наследовать от прямоугольника.
Классы — это абстракции. У них есть свои собственные свойства, которые отличаются от математических объектов и которые делают невозможным наследование.
Классы
Гради Буч так определяет ООП:
Объектно-ориентированное программирование — это методология программирования, основанная на представлении программы в виде совокупности объектов, каждый из которых является экземпляром определенного класса, а классы образуют иерархию наследования.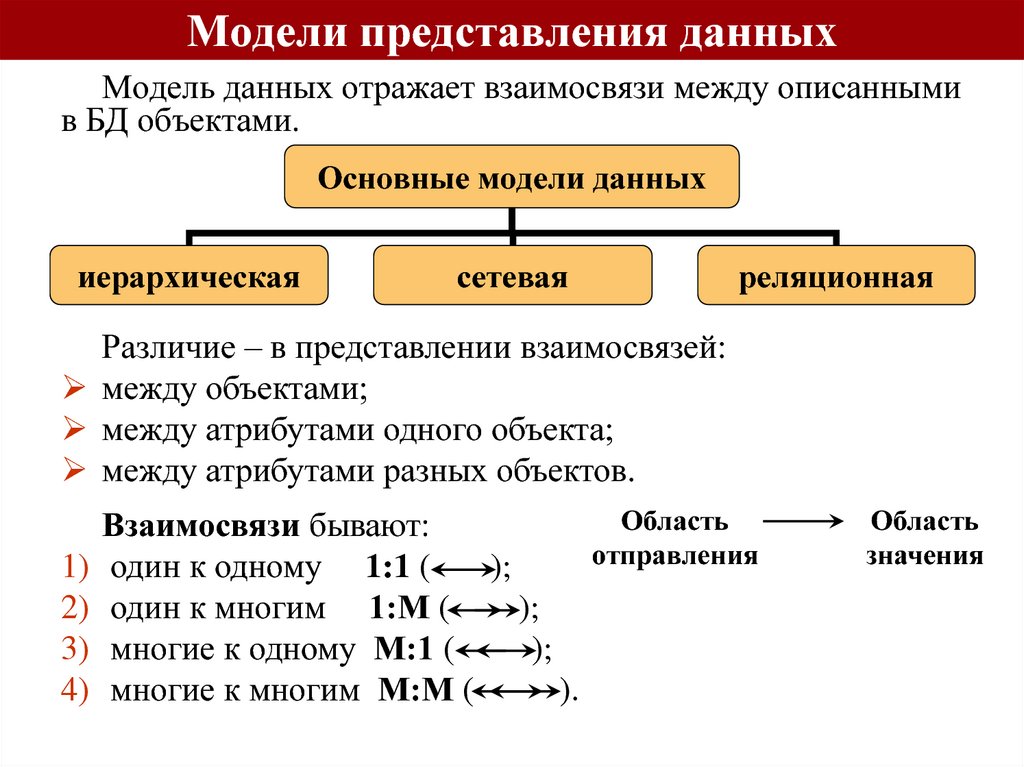
В этом определении самый важный момент — это иерархия наследования. Потому что именно наследование отличает ООП от всех других методологий.
Два основных принципа человеческого мышления — это группировка и обобщение. Классы — это, по сути, абстракции механизмов группировки и обобщения человеческого мозга. Естественно, со своими побочными эффектами и барьером. При этом группировка достигается тем, что похожим объектам сопоставляется один класс, а обобщение в ООП достигается за счет иерархии классов. Иерархии классов реализуются через полиморфизм.
ООП, кстати, интересно еще хотя бы и тем, что это, пожалуй, последняя парадигма программирования на данный момент, которая поддерживается на аппаратном уровне.
Главный побочный эффект классов — они отражают опыт, стереотипы, предубеждения того программиста, который их написал. Отсюда следует, что разные люди получат разный набор классов для одной и той же задачи. Более того, один и тот же человек, решая одну и туже задачу, но в разные моменты времени, получит разный набор классов, просто потому что его жизненный опыт меняется.
Второй побочный эффект, который стоит отметить — чужой код всегда менее понятный, чем свой собственный.
Разберемся почему так происходит. Когда человек пишет код, для него естественнее двигаться снизу вверх — от более низкоуровневых компонент к более высокоуровневым. Сначала написали один класс, потом второй, который зависит от первого, затем третий, который зависти от первого и второго, четвертый — от третьего и т.д.
Когда же человек пытается понять чужой код, он как раз двигается наоборот — сверху вниз. То есть сначала понимает общую суть, затем разбивает на компоненты, потом пытается понять суть каждого компонента и т.д. Часто эти движения мысли снизу вверх и сверху вниз у разных людей не совпадают. Естественно, что изучающему чужой код было бы легче, если разбиение кода на компоненты совпадало с его собственными убеждениями, как надо делать. Если это не так, придется затрачивать определенные усилия, чтобы понять ход мыслей разработчика. Поэтому, когда кто-то говорит, что здесь «полный хардкод», но если я перепишу, то будет все проще и понятнее. Это всегда 100% правда… Но только для него, для остальных ценность переписывания уже не так очевидна.
Это всегда 100% правда… Но только для него, для остальных ценность переписывания уже не так очевидна.
Кстати, если ничего не предпринимать специально, то при разработке снизу вверх, код становится сильно связанным между собой, то есть не повторно используемым. Чтобы побороть этот эффект надо следовать принципу инверсии зависимостей (The Dependency Inversion Principle).
Проиллюстрируем как проявляется описанный побочный эффект на простом примере. Многие жители крупных городов закупаются в крупных супермаркетах. Предположим, что жена отправляет мужа за покупками и, чтобы он не забыл, как обычно, чего-нибудь, составляет список «для тех кто в танке».
Постараемся проследить ход ее мыслей:
— Так чего я сегодня буду готовить на ужин?
— Надо приготовить чего-нибудь вкусненькое, чтобы побаловать ребенка.
— Так, нужна будет мука, молоко.
— Кажется в миксере сели батарейки.
— Стоп! Ребенку нужны витамины. Морковь. Буду делать морковный сок. и мандарины. Скоро же Новый год!
и мандарины. Скоро же Новый год!
— А хлеб дома есть? Нет, кажется, нет.Значит, надо купить!
— Еще надо купить масло.
— Забыла про ребенка — витамины. Купить яблоки.
— Чего-то ручка плохо пишет. Наверное скоро кончатся чернила. Надо купить!
— Так, ребенку надо купить сока.
— А еще игрушку — пусть порадуется.
— Картошка у нас есть на борщ? На борщ хватит, но на неделю нет. Значит тоже надо купить.
— Чуть не забыла учительница просила принести две тетради.
— К борщу нужна сметана.
— Вроде сахар кончился.
— Ребенок любит виноград.
— И еще надо купить бутилированной воды.
В итоге получаем следующий список:
- мука
- молоко
- батарейки
- морковь
- мандарины
- хлеб
- масло
- яблоки
- ручка
- сок
- игрушка
- картофель
- тетради
- сметана
- сахар
- виноград
- вода
Когда приходит муж в магазин то, что он обнаруживает? Указанные в списке товары оказываются в разных частях магазина.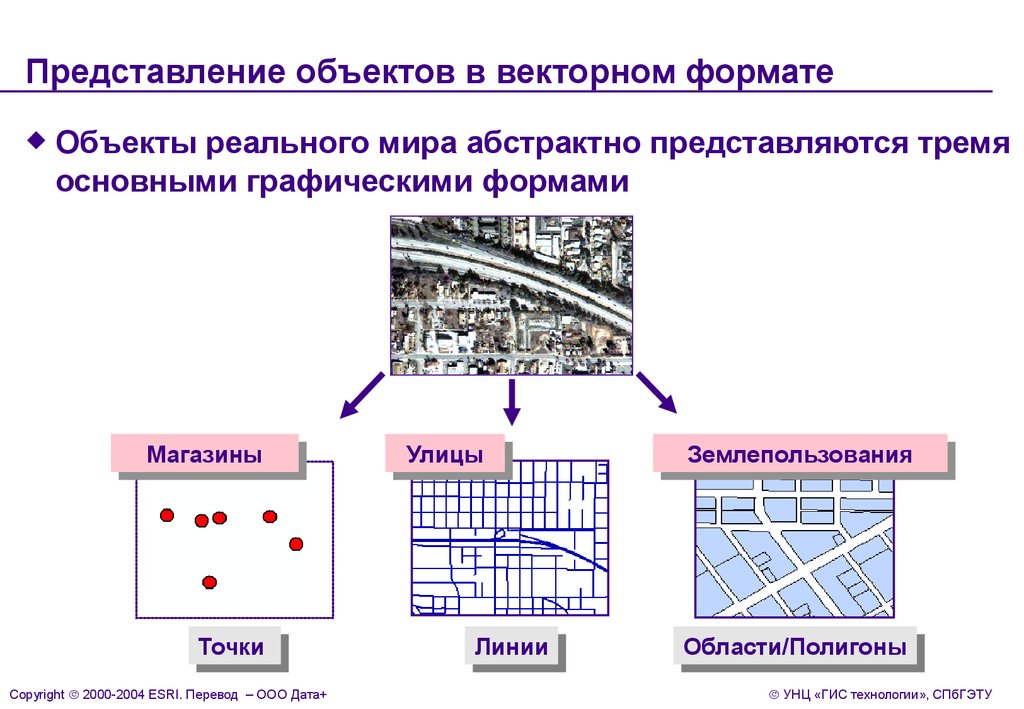 Обычно список длинный, поэтому запомнить что-либо, что было уже куплено достаточно трудно. На это накладывается, что какие-то отделы временно закрыты — идет выгрузка товаров, какого-то товара нет в продаже, плюс толчея, зимняя одежда. Более опытные товарищи ходят с карандашом или ручкой с очень озабоченным видом и постоянно смотрят в свой список. Но, в итоге, все равно, что-нибудь да забудешь купить. По своему опыту могу сказать, что это «что-нибудь» окажется самым важным, из-за чего вообще и стоило ехать в магазин.
Обычно список длинный, поэтому запомнить что-либо, что было уже куплено достаточно трудно. На это накладывается, что какие-то отделы временно закрыты — идет выгрузка товаров, какого-то товара нет в продаже, плюс толчея, зимняя одежда. Более опытные товарищи ходят с карандашом или ручкой с очень озабоченным видом и постоянно смотрят в свой список. Но, в итоге, все равно, что-нибудь да забудешь купить. По своему опыту могу сказать, что это «что-нибудь» окажется самым важным, из-за чего вообще и стоило ехать в магазин.
Какой список был бы удобен мужу? Тот, в котором все товары сгруппированы по отделам, отдельные группы идут в очередности, соответствующей порядку обхода магазина. Например, для магазина, в который хожу я было бы удобно сгруппировать товары следующим образом:
- Батарейки
- Детские тетради
- Ручка
- Вода
- Сок
- Сахар
- Морковь
- Апельсины
- Яблоки
- Виноград
- Картофель
- Масло
- Хлеб
- Молоко
- Сметана
- Мука
- Детская игрушка
Еще одно важное наблюдение — невозможно по самим абстракциям определить насколько удачными они получились. Это можно сделать, только если мы попытаемся их использовать на практике. И тут уж выясняется, что одни абстракции лучше подходят для задачи, а другие — хуже. А если еще немного изменить исходные условия, то и прежний «хороший» набор абстракций уже может не работать. Например, второй список покупок из примера перестанет работать, если прийти с ним в другой магазин с иным порядком выкладки товаров. Он станет ничем не лучше, чем первый.
Это можно сделать, только если мы попытаемся их использовать на практике. И тут уж выясняется, что одни абстракции лучше подходят для задачи, а другие — хуже. А если еще немного изменить исходные условия, то и прежний «хороший» набор абстракций уже может не работать. Например, второй список покупок из примера перестанет работать, если прийти с ним в другой магазин с иным порядком выкладки товаров. Он станет ничем не лучше, чем первый.
Отсюда вывод — невозможно придумать набор классов, который подойдет на все случаи жизни. В статье The Open-Closed Principle это называется стратегическая замкнутость.
Естественный вопрос, а как сразу создавать хорошие абстракции. Увы, но на этот счет нет точного ответа. Зато со временем выработался набор практик, который говорит, как надо поступать, и обещает, что в этом случае будет хороший результат. К таким практикам относится рефакторинг, стандарты кодирования, code review, объектная гимнастика и т.д. Цель данных практик — направить ход мыслей группы разработчиков в одном направлении, тогда шансов, что чужой код будет понятнее, станет больше. Отношение к каждой из практик у отдельно взятого человека зависит лишь от приобретенного им опыта использования практики. Часто слова «Это не работает» надо интерпретировать как «Я пробовал — у меня не получилось». Нет никаких объективных аргументов «ЗА», равно как и «ПРОТИВ».
Отношение к каждой из практик у отдельно взятого человека зависит лишь от приобретенного им опыта использования практики. Часто слова «Это не работает» надо интерпретировать как «Я пробовал — у меня не получилось». Нет никаких объективных аргументов «ЗА», равно как и «ПРОТИВ».
Так зачем нужно тогда ООП?
Проведем параллели между естественным языком и ООП
| естественный язык | ООП |
|---|---|
| Слово | класс |
| Правила | Синтаксис |
| Жанр | Архитектура |
| литературные приемы | паттерны |
Любые свои мысли человек выражает словами естественного языка. Есть два типа задач:
- Для решения надо хорошо знать сам язык. Например, чтобы написать Войну и Мир.
- Сложность не зависит от языка. Неважно сколько и какие языки Вы знаете. Это никак не помогает при решении.
 Например, теорема Ферма.
Например, теорема Ферма.
ООП — это инструмент, который создавался с прицелом на большие по размеру программы. Но, это всего лишь один из инструментов, который потребуется, чтобы написать крупный проект.
Меня всегда удивляют, статьи в стиле Почему я люблю X или Почему я не люблю X. Все прекрасно понимают, что X — инструмент. Ведь нет же таких статей про лопату. Хотя, кто знает, ведь ООП существует несколько десятилетий, а лопата несколько тысяч, и быть может где-нибудь в в каменном веке шли жестокие холивары на тему, что лучше лопатка мамонта или мотыга из камня?
Литература по теме
1. Гради Буч Объектно-ориентированный анализ и проектирование с примерами приложений на С++
Данная книга в представлении не нуждается. Одна из наиболее цитируемых книг по программированию.
2. Барбара Минто Принципы Пирамиды Минто.
Работая консультантом McKinsey Барбара Минто создала свой собственный метод написания аналитических документов, основанный. на том, как человек воспринимает информацию. В книге достаточно много места уделено принципам группировки и обобщения.
на том, как человек воспринимает информацию. В книге достаточно много места уделено принципам группировки и обобщения.
3. Роберт Мартин (Uncle Bob)
Роберт Мартин написал серию статей и книг про принципы ООП. Наиболее известные из них S.O.L.I..D. На русском языке вышла книжка Роберт Мартин Быстрая разработка программ. Принципы, примеры, практика, в которой описаны эти принципы. Но на мой взгляд про них лучше прочитать в статьях The Single Responsibility Principle, The Open-Closed Principle, The Liskov Substitution Principle, The Interface Segregation Principle, The Dependency Inversion Principle.
Принципы проектирования сложных объектов
При проектировании сложных объектов используются следующие принципы [5]:
– декомпозиция и иерархичность построения описаний объектов проектирования;
– многоэтапность и итерационность процесса проектирования;
– типизация и унификация проектных решений.
Описания технических объектов должны быть по сложности согласованы: 1) с возможностями восприятия человеком; 2) с возможностями оперирования описаниями в процессе их преобразования с помощью имеющихся средств проектирования.
Выполнить это требование в рамках единого описания удается лишь для простых изделий. Как правило, требуется структурирование описаний и соответствующее разбиение представлений об объекте на иерархические уровни и аспекты. Это позволяет распределить работы по проектированию сложных объектов между подразделениями проектировщиков, что способствует повышению эффективности и производительности труда.
Разделение описаний по степени детализации отображаемых свойств и характеристик объекта лежит в основе блочно-иерархического подхода к проектированию и приводит к появлению иерархических уровней (уровней абстрагирования) в представлениях об объекте.
На уровне 0 (верхнем уровне) сложный объект рассматривается как система из взаимно связанных и взаимодействующих элементов на уровне 1 (рис. 2.2).
Рис. 2.2 – Иерархические уровни описаний проектируемых объектов
Каждый из элементов в описании уровня 1 представляет собой также довольно сложный объект, который, в свою очередь, рассматривается как описание системы на уровне 2.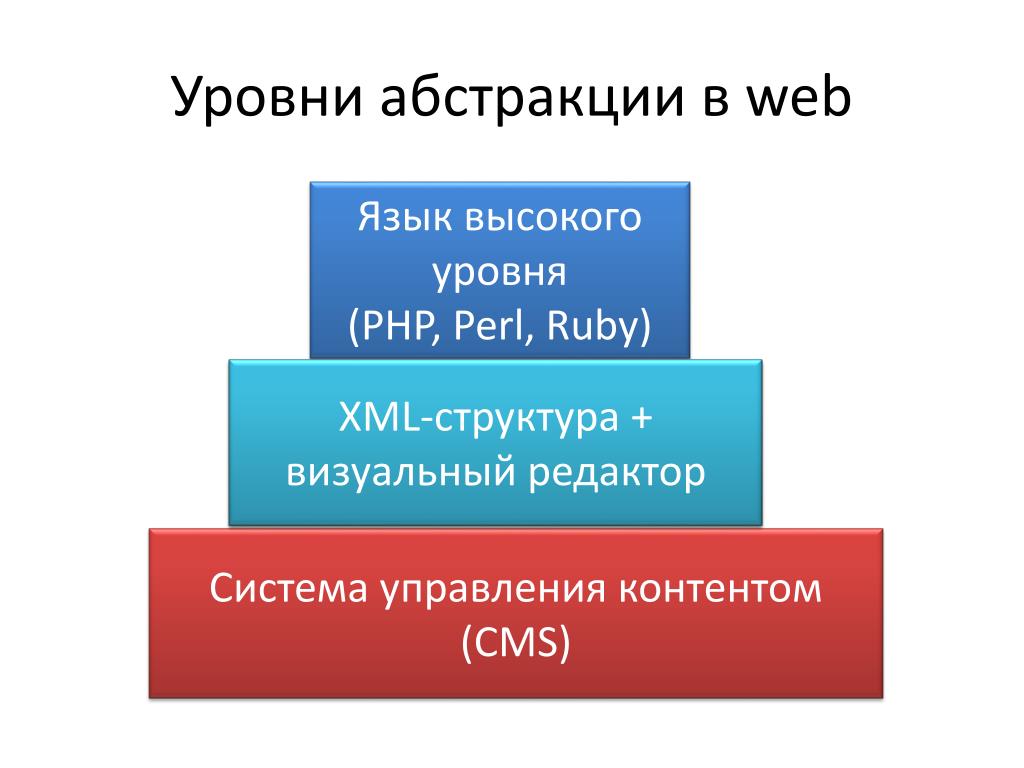 Элементами системы являются объекты , , где – количество элементов в описании системы . Как правило, выделение элементов происходит по функциональному признаку.
Элементами системы являются объекты , , где – количество элементов в описании системы . Как правило, выделение элементов происходит по функциональному признаку.
Подобное разбиение продолжается вплоть до получения на некотором уровне элементов, описания которых дальнейшему делению не подлежат, то есть до элементов, описание которых уже известно. Такие элементы по отношению к объекту называются базовыми элементами.
Принцип иерархичности означает структурирование представлений об объекте проектирования по степени детальности описаний (уровни описаний – по вертикали)
Принцип декомпозиции (блочности) означает разбиение представлений каждого уровня на ряд составных частей (блоков) с возможностью раздельного (поблочного) проектирования объектов на уровне 1, объектов на уровне 2 и т.д.
Кроме разбиения описаний по степени подробности отражения свойств объектов используют декомпозицию описаний по характеру отображаемых свойств объекта. Такая декомпозиция приводит к появлению ряда аспектов описаний. Наиболее крупные аспекты описаний объектов: функциональный; конструкторский; технологический. Решение задач, связанных с преобразованием или получением описаний, относящихся к этим аспектам, называют соответственно функциональным, конструкторским и технологическим проектированием.
Такая декомпозиция приводит к появлению ряда аспектов описаний. Наиболее крупные аспекты описаний объектов: функциональный; конструкторский; технологический. Решение задач, связанных с преобразованием или получением описаний, относящихся к этим аспектам, называют соответственно функциональным, конструкторским и технологическим проектированием.
Функциональный аспект связан с отображением основных принципов функционирования, характера физических и информационных процессов, протекающих в объекте. Функциональный аспект отображается в принципиальных, функциональных, структурных и других схемах и сопровождающих их документах.
Конструкторский аспект связан с реализацией результатов функционального проектирования, то есть с определением геометрических форм объектов и их взаиморасположением в пространстве.
Технологический аспект относится к реализации результатов функционального и конструкторского проектирования, т.е. связан с описанием методов и средств изготовления объектов.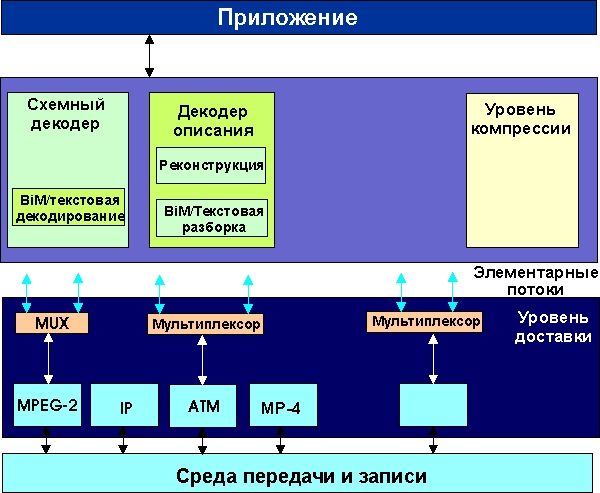
Внутри каждого аспекта возможно свое специфическое выделение иерархических уровней.
Если решение задач высоких иерархических уровней предшествует решению задач более низких иерархических уровней, то проектирование называют нисходящим. Если раньше выполняются этапы, связанные с низшими иерархическими уровнями, то проектирование называют восходящим. У каждого из этих двух видов проектирования имеются преимущества и недостатки.
При нисходящем проектировании система разрабатывается в условиях, когда ее элементы еще не определены и, следовательно, сведения о их возможностях и свойствах носят предположительный характер.
При восходящем проектировании, наоборот, элементы проектируются раньше системы, и, следовательно, предположительный характер имеют требования к системе. В обоих случаях из-за отсутствия исчерпывающей исходной информации имеют место отклонения от возможных оптимальных технических результатов.
Поскольку принимаемые предположения могут не оправдаться, часто требуется повторное выполнение проектных процедур предыдущих этапов после выполнения проектных процедур последующих этапов. Такие повторения обеспечивают последовательное приближение к оптимальным результатам и обуславливают итерационный характер проектирования. Следовательно, итерационность нужно относить к важным принципам проектирования сложных объектов.
На практике обычно сочетают восходящее и нисходящее проектирование. Например, восходящее проектирование имеет место на всех тех иерархических уровнях, на которых используются унифицированные (стандартные) элементы. Очевидно, что унифицированные элементы, ориентированные на применение в ряде различных систем определенного класса, разрабатываются раньше, чем та или иная конкретная система из этого класса.
Обычно унификация объектов имеет целью улучшение технико-экономических показателей производства и эксплуатации изделий. Использование типовых и унифицированных проектных решений приводит так же к упрощению и ускорению проектирования.
Использование типовых и унифицированных проектных решений приводит так же к упрощению и ускорению проектирования.
Однако, унификация целесообразна только в таких классах объектов, в которых из сравнительно небольшого числа разновидностей элементов предстоит проектирование и изготовление большого числа систем. Именно эти разновидности элементов подлежат унификации.
Для сложных систем и для элементов, реализующих новые физические принципы или технологические возможности, в каждом конкретном случае приходится заново выполнять многоуровневое иерархическое проектирование.
В этих условиях целесообразно ставить вопрос не об унификации изделий, а об унификации средств их проектирования и изготовления, в частности об унификации проектных процедур в рамках систем автоматизированного проектирования (САПР).
Наличие средств автоматизированного выполнения типовых проектных процедур позволяет оперативно создавать проекты новых изделий, а в сочетании со средствами изготовления в условиях гибких автоматизированных производств осуществлять оперативное изготовление новых оригинальных изделий.
Окончательное описание проектируемого объекта представляет собой полный комплект схемной, конструкторской и технологической документации, оформленной в соответствии с требованиями ГОСТов: ЕСКД (единая система конструкторской документации), ЕСТД (единая система технологической документации), ЕСПД (единая система программной документации). Этот комплект документации предназначен для использования в процессе изготовления и эксплуатации объекта проектирования.
Важное значение в этих описаниях имеют математические модели объектов проектирования, так как выполнение проектных процедур при автоматизированном проектировании основано на оперировании математическими моделями.
Математическая модель (ММ) технического объекта – система математических объектов (чисел, переменных, матриц, множеств и т.п.) и отношений между ними, отражающих некоторые свойства технического объекта.
При проектировании используют математические модели, отражающие свойства объекта, существенные с позиции проектировщика.
Среди свойств объекта, отражаемых в описаниях на определенном иерархическом уровне, в том числе в ММ, различают свойства: систем; элементов систем и внешней среды, в которой должен функционировать объект. Количественное выражение этих свойств осуществляется с помощью величин, называемых параметрами. Величины, характеризующие свойства системы, элементов системы и внешней среды, называют соответственно входными, внутренними и внешними параметрами.
Однако существование ММ не означает, что она известна разработчику и может быть представлена в явном функциональном виде. Типичной является ситуация, когда математическое описание процессов в проектируемом объекте задается моделью в форме системы уравнений, в которой фигурирует вектор фазовых переменных. Фазовые переменные характеризуют физическое или информационное состояние объекта, а их изменения во времени выражают переходные процессы в объекте. Например, состояние некоторой фирмы можно определить такими фазовыми переменными: сырье, материалы, финансовые и трудовые ресурсы.
Выделим следующие особенности параметров в моделях проектируемых объектов:
1. Внутренние параметры в моделях -го иерархического уровня становятся выходными параметрами в моделях более низкого ( )-го иерархического уровня. Так, например, трудовые ресурсы являются внутренними при проектировании производственной фирмы и в то же время выходными при проектировании отдела кадров этой фирмы.
2. Выходные параметры или фазовые переменные, фигурирующие в модели одной из подсистем (в одном из аспектов описаний), часто оказываются внешними параметрами в описании других подсистем (других аспектов). Так, например, выходные параметры подсистемы планирования выпуска продукции некоторой компании являются внешними параметрами подсистемы материально-технического снабжения этой компании.
3. Большинство выходных параметров объекта являются функционалами.
4. В техническом задании на проектирование должны фигурировать величины, называемые техническими требованиями к выходным параметрам (нормами выходных параметров). Данные нормы представляют собой границы допустимых диапазонов изменения выходных параметров.
Данные нормы представляют собой границы допустимых диапазонов изменения выходных параметров.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор…
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между…
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
К ЗАДАЧЕ ПРОЕКТИРОВАНИЯ
Изобретательство К ЗАДАЧЕ ПРОЕКТИРОВАНИЯ
просмотров — 139
БЛОЧНО-ИЕРАРХИЧЕСКИЙ ПОДХОД
ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ
При описании процесса проектирования применяют следующие понятия.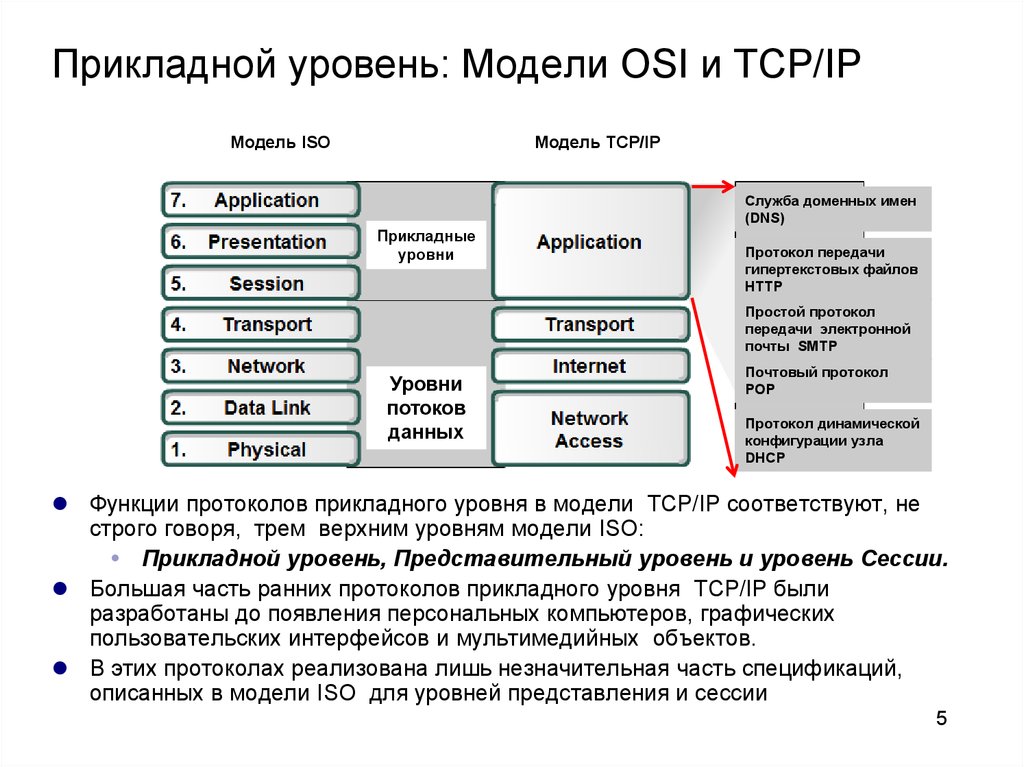
ПРОЕКТНОЕ РЕШЕНИЕ — промежуточное или окончательное описание объекта проектирования технической документацией заданной формы, крайне важное и достаточное для окончания проектирования или выбора путей его продолжения.
ТИПОВОЕ ПРОЕКТНОЕ РЕШЕНИЕ – известное проектное решение, хорошо проверенное в предыдущих разработках и используемое в процессе проектирования.
ЧАСТНОЕ ПРОЕКТНОЕ РЕШЕНИЕ – промежуточное описание объекта проектирования, частично удовлетворяющее требованиям задания на проектирование.
ПРОЕКТНЫЙ ДОКУМЕНТ – документ, выполненный по заданной форме, в котором содержится какое-либо проектное решение.
Описание объекта проектирования производится заданием его характеристик и их числовыми значениями или параметрами. Параметры подразделяются на входные, выходные, внутренние и внешние. Значения входных сигналов, питающих напряжений относятся к группе входных параметров. Значения выходных характеристик составляют группу выходных параметров. По этим параметрам можно судить о правильности работы системы, в связи с этим они являются показателями качества. Внутренние параметры — ϶ᴛᴏ значения характеристик элементов проектируемого изделия. Внешние параметры – значения характеристик внешней среды, влияющих на функционирование объекта.
По этим параметрам можно судить о правильности работы системы, в связи с этим они являются показателями качества. Внутренние параметры — ϶ᴛᴏ значения характеристик элементов проектируемого изделия. Внешние параметры – значения характеристик внешней среды, влияющих на функционирование объекта.
Совокупность характеристик, описывающих состояние объекта͵ называют фазовыми переменными. Фазовые переменные являются функциями независимых переменных, к примеру, времени или частоты.
Постоянное развитие науки и техники приводит к появлению все более сложных технических объектов – сложных систем, состоящих из большого количества
взаимодействующих элементов. Это означает, что описание системы содержит количество информации, восприятие которой недоступно для одного человека. По этой причине объект проектирования, рассматриваемый как сложная система, разбивается на элементы, выделяются связи между элементами и указываются отношения на связях. В случае если какие-либо элементы при первом разбиении оказываются сложными, то они рассматриваются как подсистемы верхнего уровня, и к ним применяется аналогичное разбиение. Этот процесс продолжается до тех пор, пока все элементы не станут простыми в том смысле, что задачи проектирования, относящиеся к ним, бывают решены одним человеком в заданный промежуток времени.
Этот процесс продолжается до тех пор, пока все элементы не станут простыми в том смысле, что задачи проектирования, относящиеся к ним, бывают решены одним человеком в заданный промежуток времени.
Такой процесс проектирования требует структурирования описаний и расчленения представлений о проектируемых объектах на иерархические уровни и аспекты. Этот подход к проектированию принято называть БЛОЧНО-ИЕРАРХИЧЕСКИМ. Он содержит иерархические уровни (уровни абстрагирования) в представлениях о проектируемом объекте.
Сложный объект S рассматривается как система S из n взаимосвязанных и взаимодействующих элементов Si . Каждый из элементов в описании уровня 1 представляет собой также довольно сложный объект, который, в свою очередь, рассматривается как система Si на уровне2. Элементами системы Si являются объекты Sij.
S
——————————————————————
1 S1 S2 … Sn
—————————————————————-
2 S11 … S1m1 S21 … S2m2
—————————————————————-
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, на самом верхнем уровне используется наименее детализированное представление, отражающее только общие черты проектируемой системы. На следующих уровнях степень подробности рассмотрения возрастает, при этом система рассматривается не в целом, а отдельными блоками. Это позволяет на каждом уровне формулировать и решать задачи приемлемой сложности, поддающиеся уяснению и пониманию человеком и решению с помощью имеющихся средств проектирования. Разделение на блоки должно быть таким, чтобы документация на блок любого уровня была обозрима и воспринимаема одним человеком.
На следующих уровнях степень подробности рассмотрения возрастает, при этом система рассматривается не в целом, а отдельными блоками. Это позволяет на каждом уровне формулировать и решать задачи приемлемой сложности, поддающиеся уяснению и пониманию человеком и решению с помощью имеющихся средств проектирования. Разделение на блоки должно быть таким, чтобы документация на блок любого уровня была обозрима и воспринимаема одним человеком.
При проектировании сложных систем выделяют следующие
уровни проектирования:
— системный,
— структурный,
— функциональный,
— схемотехнический,
— функциональный.
На системном уровнеформулируются требования к проектируемому объекту как системе, взаимодействующей с элементами системы более высокого уровня. На структурном уровне объект проектирования разбивают на структурные блоки. К примеру, персональная ЭВМ разбивается на системный блок, устройства ввода – вывода информации. Согласуются параметры сигналов между блоками.
К примеру, персональная ЭВМ разбивается на системный блок, устройства ввода – вывода информации. Согласуются параметры сигналов между блоками.
На функциональном уровне системные блоки разбиваются на функциональные модули, и их функционирование описывается математическими соотношениями. На схемотехническом уровне описание функционального модуля детализируют до уровня компонентов и проводят расчет сигналов с учетом их временных характеристик. На компонентном уровне решают задачу замещения компонентов, полученных в результате схемотехнического проектирования на серийно выпускаемые компоненты.
Составные части этапа проектирования называют проектными процедурами. Более мелкие составные части процесса проектирования, входящие в состав проектных процедур, называют проектными операциями.
При блочно-иерархическом подходе к проектированию задача большой размерности – проектирование сложной системы – разбивается на группы задач малой размерности, причем внутри групп разные задачи могут решаться параллельно. На каждом уровне имеются свои представления о системе и элементах. То, что на более высоком i — м уровне называлось элементом, на следующем (i-1) – м уровне становится системой. Часто элементы самого низшего из уровней называются базовыми элементами или компонентами. Разработчики, участвующие в проектировании, имея дело со сложными системами некоторого уровня; всегда решают задачу проектирования простых элементов, которые входят в состав сложных систем.
На каждом уровне имеются свои представления о системе и элементах. То, что на более высоком i — м уровне называлось элементом, на следующем (i-1) – м уровне становится системой. Часто элементы самого низшего из уровней называются базовыми элементами или компонентами. Разработчики, участвующие в проектировании, имея дело со сложными системами некоторого уровня; всегда решают задачу проектирования простых элементов, которые входят в состав сложных систем.
В процессе проектирования сложных объектов, как правило, приходится оперировать описаниями, в которых одновременно представлены два иерархических уровня, к примеру, i и ( i +1). В таких случаях применяют термины система, подсистема и элементы, относя их соответственно к системе i — го уровня, системам и элементам (i +1) – го уровня.
Совокупность описаний некоторого уровня вместе с постановками задач и методами получения этих описаний называют иерархическим уровнем проектирования.
БЛОЧНО-ИЕРАРХИЧЕСКИЙ ПОДХОД
ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ
При описании процесса проектирования применяют следующие понятия. ПРОЕКТНОЕ РЕШЕНИЕ — промежуточное или окончательное описание объекта проектирования технической документацией заданной формы,… [читать подробенее]
ПРОЕКТНОЕ РЕШЕНИЕ — промежуточное или окончательное описание объекта проектирования технической документацией заданной формы,… [читать подробенее]
Языки программирования по уровню абстракции
Содержание
- Уровни абстракций — ключ к пониманию архитектурных изысков ПО
- Модель объекта и ступень приближения
- Построение структуры
- Абстракция и Реализация
- 21. Языки программирования. Классификация ЯП
- Классификация языков программирования
- По системе типов
- По уровню абстракции
- По модели исполнения
- Классификация по “поколению”
- Уровень абстракции (программирование)
- Многоуровневая абстракция
- Многоуровневая абстракция
- Зачем вообще делят на уровни абстракции?
- Многоуровневая абстракция работы с данными
- Когда возникают проблемы?
- Что делать?
- Чем кодогенерация может помочь в сложных моделях
- Кодогенерация + многоуровневая абстрактная модель
- Языковые абстракции
- 3.
 1. Отступление «об абстрагировании»
1. Отступление «об абстрагировании» - Видео
Уровни абстракций — ключ к пониманию архитектурных изысков ПО
Эта статья будет в большей степени полезна новичкам, только начинающим работать с абстракциями и построением архитектур ПО. Однако искренне надеюсь, что и более опытные специалисты смогут найти для себя что-то интересное в этом материале, — пишет Наталия Ништа в своей статье, опубликованной на DOU.UA.
Абстракция — один из набивших оскомину столпов ООП. В любом курсе по программированию с вероятностью 99% можно найти урок-другой, посвященный теме абстракции. И практически всегда упускается более широкое, всеобъемлющее понятие «уровней абстракции» — на мой взгляд, критически важное, ключевое для понимания всех остальных принципов проектирования.
Модель объекта и ступень приближения
Абстракция — это модель некоего объекта или явления реального мира, откидывающая незначительные детали, не играющие существенной роли в данном приближении. И уровень абстракции — это и есть наша ступень приближения. Каждый человек способен строить абстракции — это отличительная способность homo sapiens. Но не каждый способен делать это достаточно качественно.
И уровень абстракции — это и есть наша ступень приближения. Каждый человек способен строить абстракции — это отличительная способность homo sapiens. Но не каждый способен делать это достаточно качественно.
Чтобы не вдаваться в многоэтажную теорию, приведу наглядный пример. Итак, раскладываем по полочкам. Представьте себе, что вы решили испечь яблочный пирог. Вы берете толстую кулинарную книгу с полки (для любителей, все остальные — в сеть), открываете нужный вам рецепт и читаете нечто следующее:
«Чтобы испечь яблочный пирог, нам понадобится два килограмма непременно свежих яблок, румяных, как девичьи щёки на крещенском морозе. Помнится, видал я такие щёчки у моей ненаглядной Лизоньки, когда мы впервые с ней встретились, и она угощала меня яблочными пирогами, состряпанными на последние деньги, которые она выручила от продажи дедовских коллекционных монет 1819 года, выпущенных при императоре таком-то…» И т.д, и т.п.
Если вы осилили текст курсивом, то вы очевидно заметили, что он имеет весьма посредственное отношение к тому, что нам нужно. Собственно, к тому, как же печь эти чертовы пироги из яблок, не правда ли?
Собственно, к тому, как же печь эти чертовы пироги из яблок, не правда ли?
А теперь вспомните, как часто в коде нам приходится встречать логические конструкции типа if-if-if-else-if-else-if, содержащие тонны вложенных рассуждений. Приходится читать все эти адские нагромождения и держать в голове всю цепочку событий, для того, чтобы понять, что тут вообще происходит и какое отношение «вот это всё» имеет к заявленному содержанию (название класса/функции по аналогии с названием рецепта «яблочный пирог»).
А ведь что на самом деле нас интересовало в рецепте? Нам нужно было знать, сколько и каких продуктов нам понадобится и что затем с ними делать. Нас абсолютно не интересует в этом приближении (на данном уровне абстракции), каким образом эти продукты к нам попали (более низкие уровни абстракции) и что мы будем делать с этим пирогом потом (более высокие уровни абстракции). Это очевидно. Но тысячи программистов продолжают игнорировать эти принципы и пишут мозговыносные структуры if-if-else-if…
А бывает так, что в рецепте встречаются умные словечки типа «бланшировать» или «сделать бизе». В хороших кулинарных руководствах описание подобных практик выносят в отдельные главы, а в самих рецептах лишь ссылаются на страницы с подробным описанием техники (привет, Инкапсуляция).
В хороших кулинарных руководствах описание подобных практик выносят в отдельные главы, а в самих рецептах лишь ссылаются на страницы с подробным описанием техники (привет, Инкапсуляция).
Построение структуры
Конечно, бывают и обратные ситуации, когда за тоннами слоёв абстракций невозможно уловить нить повествования. Но в этом-то и состоит мастерство архитектора ПО — спроектировать достаточно простую для сопровождения, то есть понимания, структуру. «Не нужно быть умным — нужно быть понятным» ©.
В то же время, не терять в эффективности решения бизнес-задач. В некоторой мере, это искусство. Каждый конкретный архитектор (программист) будет рисовать эту картину, то есть создавать модель мира по-своему: «Я художник — я так вижу». Вот вам пища в топку холиваров на счет единых стандартов программирования в рамках команды и необходимости наличия исполнителя роли архитектора.
Абстракция и Реализация
Есть ещё один момент, о котором я хочу упомянуть: путешествие между слоями логик. Красиво изолированный уровень абстракции достаточно прост для понимания: у нас есть ряд объектов, очевидным образом взаимодействующих между собой, уровни вложенности маленькие (если они вообще есть — как в рецепте пирога). Однако, как нам уже стало понятно, самым трудозатратным для понимания является перемещение между уровнями абстракций.
Красиво изолированный уровень абстракции достаточно прост для понимания: у нас есть ряд объектов, очевидным образом взаимодействующих между собой, уровни вложенности маленькие (если они вообще есть — как в рецепте пирога). Однако, как нам уже стало понятно, самым трудозатратным для понимания является перемещение между уровнями абстракций.
Чтобы упростить этот процесс, стоит разобраться в природе дуальности понятий Абстракции и Реализации. В этом моменте обычно и фокусируются на различных курсах по программированию, перед этим упуская понятие уровня абстракции. Из-за чего у студентов формируется заблуждение, что ООП — это что-то запредельно сложное.
Возьмем для примера такую цепочку слоёв абстракций: нам нужен пирог для Дня рождения друга. Спускаемся ниже: пирог может быть фруктовый или мясной. А может, рыбный? В момент рассуждений о том, что нам нужен какой-то пирог в качестве подарка, он (пирог) выступает конечным элементом данного уровня абстракции. В этот момент пирог — это реализация подарка (но он может быть любой: бритва, деньги, конструктор лего — это всё варианты подарка). Когда мы совершаем переход на более низкий уровень абстракции, наш объект (пирог) превращается из конечной реализации в абстракцию: уже нас не устраивает уровень детализации «какой-то пирог», мы начинаем искать его реализацию (привет, Полиморфизм).
Когда мы совершаем переход на более низкий уровень абстракции, наш объект (пирог) превращается из конечной реализации в абстракцию: уже нас не устраивает уровень детализации «какой-то пирог», мы начинаем искать его реализацию (привет, Полиморфизм).
Таким образом, считать объект абстрактным или реальным — зависит исключительно от степени детализации моделируемого «мира» и от бизнес-задач, поставленных перед архитектором. И, разумеется, от его чувства прекрасного.
С моей точки зрения, понимая явление уровней абстракций, можно легко разобраться во всех принципах и шаблонах проектирования.
Источник
21. Языки программирования. Классификация ЯП
Язык программирования – это искуственный язык, созданный для взаимодействия с машиной, в частности, с компьютером. ЯП используются для написания программ, которые управляют машиной и/или выражают алгоритмы.
Первые ЯП были созданы задолго до появления компьютеров и управляли поведением, скажем, самоиграющих пианино или автоматических ткацких станков.
Многие ЯП имеют императивную форму, т.е. описывают последовательность операций. Другие могут иметь декларативную форму, т.е. описывают результат, а не то, как его получить.
Некоторые языки определяются стандартом (C,C++,Haskell, и др.). Другие не имеют формального описания, и наиболее широко распространенная реализация используется в качестве эталона.
Описание ЯП обычно делится на две части: синтаксис, т.е. форма, и семантика, т.е. значение.
Семантика в свою очередь подразделяется на лексику и грамматику.
Лексика определяет какие “слова” могут быть в языке. Это включает названия переменных, функций, числовые константы, строки, и т.п., а так же управляющие символы языка. Грамматика определяет каким образом эти “слова” комбинируются в более сложные выражения.
Не все синтаксически корректные программы являются семантически корректными. Например:
Семантика же подразделяется на статическую, динамическую, и систему типов.
определяет статические свойства языка, выходящие за рамки синтаксиса. Например, статическая семантика может определять, что все идентификаторы должны быть определены перед использованием, или что вызов функции должен принимать столько же аргументов, сколько указано в ее определении (ни то ни другое не является обязательным, кстати сказать)
Например, статическая семантика может определять, что все идентификаторы должны быть определены перед использованием, или что вызов функции должен принимать столько же аргументов, сколько указано в ее определении (ни то ни другое не является обязательным, кстати сказать)
определяет стратегию выполнения программы. Она определяет, каким образом исполняются инструкции, порядок их исполнения, значение управляющих структур и т.д.
определяет каким образом ЯП классифицирует значения и выражения, как эти типы взаимодействуют и каким образом ЯП может манипулировать ими. Система типов является практическим приложением теории категорий. Цель системы типов – проверка программы на корректность (до какой-то степени). Любая система типов, отвергая некорректные программы, будет так же отвергать некоторый процент коррекнтых (хотя необычных) программ. Чтобы обойти это ограничение, ЯП обычно имеют некие механизмы для выхода из ограничений системы типов. В большинстве случаев, указание корректных типов ложится на совесть программиста. Однако некоторые ЯП (обычно функциональные) умеют выводить типы исходя из семантики, и таким образом освобождают программиста от необходимости явно указывать типы.
Однако некоторые ЯП (обычно функциональные) умеют выводить типы исходя из семантики, и таким образом освобождают программиста от необходимости явно указывать типы.
Классификация языков программирования
Существует множество критериев, по которым можно классифицировать языки программирования. Частые варианты классификации включают:
Четкой классификации не существует, по той простой причине, что существуют буквально тысячи ЯП, и в любой категории классификации обнаруживается практически непрерывный спектр.
По системе типов
Наиболее категоричное разделение ЯП по системе типов на типизированные и нетипизированные.
Нетипизированные языки позволяют производить любую возможную операцию над любыми данными. Это обычно какие-либо языки ассемблера, которые работают непосредственно с двоичным представлением данных в памяти.
С точки зрения теории типов очень немногие из современных языков являются типизированными в полном смысле этого слова. Большинство являются типизированными в некоторой мере. Так, многие языки позволяют выходить за пределы системы типов, принося типобезопасность в жертву более точному управлению исполнением программы.
Так, многие языки позволяют выходить за пределы системы типов, принося типобезопасность в жертву более точному управлению исполнением программы.
Типизированные языки определяют типы данных, с которыми работает любая операция. Например, операция деления работает над числами – для строк эта операция не определена.
Типизированные языки, в свою очередь, могут классифицироваться по моменту проверки типов и по строгости этой проверки.
По моменту проверки типов ЯП делятся на статически и динамически типизированные (или просто, статические и динамические).
Статически типизированные языки
При статической типизации, типы всех выражений точно определены до выполнения программы, и обычно проверяются при компиляции. Языки со статической типизацией, в свою очередь могут быть явно типизированными (manifestly typed) или типовыводящими (type-inferred).
Явно типизированные языки
требуют явного указания типов. К ним относятся, например, C, C++, C#, Java.
определяют (выводят) типы большинства выражений автоматически, и требуют явного аннотирования только в сложных и неоднозначных случаях. К ним относятся, например, Haskell и OсaML.
К ним относятся, например, Haskell и OсaML.
Надо заметить, что многие явно типизированные языки умеют выводить типы в некоторых случаях (например, auto в С++11), поэтому четкую грань здесь провести можно не всегда.
Динамически типизированные языки
производят проверку типов на этапе выполнения. Иначе говоря, типы связаны со значением при выполнении, а не с текстовым выражением. Как и типовыводящие языки, динамически типизированные не требуют указания типов выражений. Помимо прочего, это позволяет одной переменной иметь значения разных типов в разные моменты исполнения программы. Однако, ошибки типов не могут быть автоматически обнаружены, пока фрагмент кода не будет выполнен. Это усложняет отладку и несколько подрывает идею типобезопасности в целом. Примерами динамически типизированных языков являются Lisp, Perl, Python, JavaScript и Ruby.
По строгости типизации языки делятся на сильно и слабо типизированные.
Слабо типизированные языки
неявно конвертируют один тип в другой, скажем, строки в числа и наоборот. Это может быть удобно в некоторых случаях, однако многие программные ошибки могут быть пропущены. Усложняется отладка.
Это может быть удобно в некоторых случаях, однако многие программные ошибки могут быть пропущены. Усложняется отладка.
Сильно типизированные языки
не позволяют неявную конверсию, и требуют явной.
В целом, четкую грань провести оказывается достаточно сложно, поскольку неявное преобразование типов в той или иной мере производится в большинстве языков. Однозначно к слабо типизированным относят Perl, JavaScript и C (в силу свободной конверсии void* ). К сильно типизированным относят C++, Java, Haskell, и другие.
По уровню абстракции
Классификация по уровню абстракции сильно зависит от современных представлений о “высоком уровне абстракции”.
Языки по-настоящему низкого уровня – это машинный код и языки ассемблера, все остальные – в некотором смысле языки высокого уровня. Тем не менее, многие сейчас считают C и C++ языками низкого уровня.
Java, Python, Ruby и т.п. сейчас общепринято считаются языками высокого уровня.
Языки высокого уровня могут значительно упрощать реализацию сложных алгоритмов, однако обычно они генерируют менее эффективный машинный код, чем языки более низкого уровня.
По модели исполнения
ЯП может быть компилируемым, транс-компилируемым или интерпретируемым.
Интерпретируемые языки исполняются непосредственно, без этапа компиляции. Программа, называемая интерпретатором, читает каждое выражение, определяет сообразное действие, и совершает его. Гибридный вариант может генерировать машинный код “на лету” и исполнять его.
Интерпретируемые языки: PHP, Perl, Bash, Python, JavaScript, Haskell
Компилируемый язык компилируется, т.е. переводится в исполнимую форму до выполнения.
Компиляция может производиться непосредственно в машинный код, или в какое-либо промежуточное представление (байт-код), которое потом интерпретируется виртуальной машиной.
Компилируемые языки (машинный код): ASM, С, С++, Algol, Fortran Компилируемые языки (байт-код): Python, Java
Транс-компилируемые языки – это языки, которые сперва переводятся в язык более низкого уровня, который в свою очередь уже может быть скомпилирован. Частой целью для транс-компилируемых языков является C, который, в свою очередь, часто является транс-компилируемым в ассемблер.
Транс-компилируемые языки: C, C++, Haskell, Fortran
Линии сильно размыты, поскольку существуют компиляторы для традиционно интерпретируемых языков, и, напротив, интерпретаторы для традиционно компилируемых.
Классификация по “поколению”
Поколение – несколько условная характеристика, которая в значительной мере связана с историей появления современных языков программирования.
Языки первого поколения
1GL – это машинные языки. Исторически, программы на этих языках вводились при помощи переключателей на передней панели ЭВМ, либо “писались” на перфокартах и позже перфолентах. Программа на 1GL состоит из 0 и 1 и сильно привязана к конкретному железу, на котором она должна исполняться.
Языки второго поколения
Это общая категория для различных языков языков ассемблера. С одной стороны, код языков 2GL может читать человек, и он должен быть конвертирован в машино-читаемую форму (этот процесс называется ассемблированием, или сборкой). С другой стороны, этот язык специфичен к процессору и прочему аппаратному окружению.
Языки третьего поколения
Более абстрактные, чем 2GL, это языки, которые перекладывают заботу о непринципиальных деталях с плеч программиста на плечи компьютера. Fortran, ALGOL и COBOL являются первыми 2GL. C, C++, Java, BASIC и Pascal так же могут быть отнесены к 3GL, хотя в общем 3GL подразумевает только структурную парадигму (в то время как C++, Java работают в том числе в ООП)
Языки четвертого поколения
Определение несколько расплывчато, однако в целом сводится к еще более высокому уровню абстракции, чем 3GL. Однако, подобный уровень абстракции часто требует сужения области применения. Так, например, FoxPro, LabView G, SQL, Simulink являются 4GL, однако находят применение в узкой специфической области. Некоторые исследователи считают, что 4GL являются подмножеством DSL (domain specific language, язык, специфичный к области).
Языки пятого поколения
В конце 80-х – начале 90-х была попытка разработать класс языков, которые “пишут программы сами”. По идее, программист должен был описывать как программа должна себя вести, а остальное должен был делать компьютер. К примерам можно отнести Prolog, OPS5, Mercury. К добру или худу, но эта затея провалилась, поскольку создание эффективного алгоритма для решения конкретной проблемы – само по себе весьма нетривиальная задача, и часто для ее решения требуются человеческая смекалка и интуиция.
К примерам можно отнести Prolog, OPS5, Mercury. К добру или худу, но эта затея провалилась, поскольку создание эффективного алгоритма для решения конкретной проблемы – само по себе весьма нетривиальная задача, и часто для ее решения требуются человеческая смекалка и интуиция.
Источник
Уровень абстракции (программирование)
Уровень абстракции предоставляет способ сокрытия деталей реализации определенного множества функциональных возможностей. Модели программного обеспечения, использующие уровни абстракции, включают семиуровневую модель OSI для протоколов передачи данных компьютерных сетей, библиотеку графических примитивов OpenGL, модель ввода-вывода на основе потоков байт из Unix, адаптированную MSDOS, Linux и большинством других современных операционных систем.
В операционной системе Unix большинство типов операций ввода-вывода рассматриваются как потоки байтов, считываемые или записываемые на устройство. Эта модель потока байтов используется для ввода-вывода в файл, сокет и компьютерный терминал, чтобы обеспечить независимость от устройства ввода-вывода. Для чтения и записи в устройство на уровне приложения программа вызывает функцию открытия устройства, которое может соответствовать реальному устройству, например, терминалу или виртуальному устройству, например, сетевому порту или файлу в файловой системе. Физические характеристики устройства передаются операционной системе, которая, в свою очередь, предоставляет абстрактный интерфейс, позволяющий программисту считывать и записывать байты в устройство. Операционная система затем выполняет действительное преобразование, необходимое для чтения и записи потока байтов в устройство.
Для чтения и записи в устройство на уровне приложения программа вызывает функцию открытия устройства, которое может соответствовать реальному устройству, например, терминалу или виртуальному устройству, например, сетевому порту или файлу в файловой системе. Физические характеристики устройства передаются операционной системе, которая, в свою очередь, предоставляет абстрактный интерфейс, позволяющий программисту считывать и записывать байты в устройство. Операционная система затем выполняет действительное преобразование, необходимое для чтения и записи потока байтов в устройство.
Большинство графических библиотек, например, OpenGL, предоставляют в качестве интерфейса абстрактную графическую модель. Библиотека отвечает за трансляцию команд, данных программистом, в специальные комадны устройства, необходимые для рисования графических элементов и объектов. Специальные команды устройства для графопостроителя отличаются от команд устройства для ЭЛТ монитора, но графическая библиотека скрывает зависящие от устройства детали реализации, предоставляя абстрактный интерфейс, содержащий набор примитивов, общеупотребимых для рисования графических объектов.
Хорошая абстракция обобщает то, что можно сделать абстрактным; допуск специфики нарушает абстракцию и ее успешное применение требует приспособления к каждому уникальному требованию или проблеме.
Часто уровни абстракции организуются в иерархию уровней абстракции. Сетевая модель OSI содержит семь уровней абстракции. Каждый уровень модели OSI ISO инкапсулирует и рассматривает отдельную часть требований по организации связи, сокращая таким образом сложность соответствующих инженерных решений.
Известный афоризм Дэвида Уилера гласит: Все проблемы в информатике можно решить на другом уровне окольным путем; [2] это часто неверно цитируется с заменой «окольного пути» на «абстракцию». Продолжение от Кевлина Хенни гласит «. за исключением проблем с большим уровнем косвенности.»
Источник
Многоуровневая абстракция
В предыдущей статье мы рассмотрели некоторые подходы к кодогенерации, теперь я хочу взглянуть на многоуровневую абстракцию и произвести некоторый анализ.
Данная статья содержит лишь теорию. Практической будет следующая статья (постараюсь чередовать).
Многоуровневая абстракция
Многоуровневая абстракция — разделение компонента приложения на несколько уровней абстракции так, что на каждом уровне абстракция согласована. Это несколько заумно может звучать. Суть в том, чтобы разделить компонент на несколько уровней, таким образом, чтобы мы могли относительно автономно работать с данным уровнем в его абстракции и не держать в голове информацию о других уровнях.
Зачем вообще делят на уровни абстракции?
1. Борьба со сложностью. На каждом уровне применяются методы именно данного уровня.
2. Уменьшение связности.
3. Обеспечение взаимозаменяемости классов на всех уровнях кроме верхнего.
Многоуровневая абстракция работы с данными
Идем по убыванию уровня абстракции:
* Класс-сущность реального мира
* Провайдер данных
* Реальные библиотеки работы с данными
Когда возникают проблемы?
1. Обычно в одном проекте несколько многоуровневых абстрактных моделей. Проблемы возникают если несколько абстрактных моделей надо подвергнуть однообразным изменениям. При этом приходится вносить изменения во все промежуточные уровни абстракции включая верхний.
Обычно в одном проекте несколько многоуровневых абстрактных моделей. Проблемы возникают если несколько абстрактных моделей надо подвергнуть однообразным изменениям. При этом приходится вносить изменения во все промежуточные уровни абстракции включая верхний.
2. При прототипировании накладные расходы на проектирование многоуровневой абстрактной модели могут быть слишком высоки и возможно написание временного кода без уровней абстракции, который придется выкинуть после утверждения прототипа.
3. Абстракция от источников данных может породить (и порой порождает) неоптимальную работу с источниками данных.
Что делать?
Кодогенерация во многих случаях (не всегда) может заменить многоуровневую абстракцию. При этом будут генерироваться конечные классы (из верхнего уровня абстракции), содержащие в себе методы работы с выбранным источником данных.
1. Имея в основе метаданные, мы можем вносить изменения в алгоритмы генерации кода и разом модифицировать всю модель.
2. При наличии метаданных прототип модели можно получить в кратчайший срок.
При наличии метаданных прототип модели можно получить в кратчайший срок.
3. За счет наличия генераторов для каждого источника данных, модель будет сгенерирована с приемлемой оптимальностью работы с выбранным источником данных, учитывая его специфику.
Чем кодогенерация может помочь в сложных моделях
Сложные приложения всегда задают много вопросов. По моим наблюдениям, на бОльшую часть из них можно ответить еще в процессе разработки (например, на сайте нужно кеширование или нет; какая операционная система будет на сервере; использовать буфферизацию вывода или нет. ). Если мы ответим на этим вопросы заранее — мы можем избежать лишней сложности программы, лишних действий, лишних проверок и т.п. Более того, кодогенератор сам может собрать в среде назначения некоторые данные заранее, которые он может использовать для оптимизации работы.
Но это не значит, что меньше результирующего кода = проще система. Кодогенератор сам должен быть достаточно качественный для того, чтобы генерировать качественный код.
Кодогенерация + многоуровневая абстрактная модель
В следующей статье мы разработаем определенный несложный кодогенератор.
Источник
Языковые абстракции
3.1. Отступление «об абстрагировании»
Абстрагирование особенно актуально для двух групп языков, которые мы определили как языки моделирования и программирования.
3.2. Абстракция данных
Исключительное использование сильно типизированного языка является фактором, в наибольшей степени определяющим возможность проектирования сложной системы в короткий срок.
Н. Вирт
3.2.1. Данные и типы данных
3.2.2. Эволюция определения типа данных
Об основном вопросе в области типов данных
3.2.3. Абстрактные типы данных
Абстрактным типом данных будем называть модуль, внутренняя часть которого скрыта от пользователя, и работа с модулем разрешается только при помощи операций.
Обоснование применимости концепции абстрактных типов данных в практике программирования было сделано Хоаром (С. A.R. Hoare). Некоторая программа, работающая с данными типа т и содержащая последовательность операторов, реализующих операции с этим типом, может быть преобразована в функционально-эквивалентную программу. В результирующей программе каждая операция с типом т может быть описана в виде функции, а все явно запрограммированные действия с этим типом могут быть заменены вызовами соответствующих функций.
A.R. Hoare). Некоторая программа, работающая с данными типа т и содержащая последовательность операторов, реализующих операции с этим типом, может быть преобразована в функционально-эквивалентную программу. В результирующей программе каждая операция с типом т может быть описана в виде функции, а все явно запрограммированные действия с этим типом могут быть заменены вызовами соответствующих функций.
3.2.4. Разновидности полиморфизма
Поясним разницу между перегрузкой и приведением на простом примере. Рассмотрим оператор сложения, применяемый к различным типам операндов:
О перегрузке
Бьерн Страуструп (Bjarne Stroustrup) в статье «Generalizing Overloading for С++ 2000» (http://www.research.att.com/-bs/papers.html), датируемой 1 апреля 1998 г., предлагает развивать идеи перегрузки в языке C++. Например, предлагается перегружать не только пробелы, но и пропущенные пробелы.
3.2.5. Статический и динамический контроль типов
Контроль типов должен выяснять возможность применения данной операции к данным аргументам.
3.2.6. Статически и динамически типизируемые языки программирования
Одним из наиболее интересных динамически типизируемых языков программирования является язык «Автокод Эльбрус» [Сафонов 1989]. При определении переменной целочисленного типа данных отводится лишь области памяти необходимого формата. Например, описание ф64 а указывает на необходимость отведения для переменной а 64-х битов, в которых далее может быть размещено целое число. Динамическая типизация может быть эффективно поддержана аппаратной реализацией (например, архитектура Эльбрус для языка «Автокод Эльбрус»).
3.3. Абстракция управления
3.3.1. Структурное программирование
3.3.2. Визуальное структурное программирование
Обратим внимание на то, что долгое время в Америке отвергалась идея визуального программирования, и основной упор там делался на создание универсального языка программирования.
3.3.3. Оператор перехода
Оператор перехода служит для того, чтобы изменить последовательность выполнения операторов программы.
3.3.4. Оператор итерации
В некоторых языках программирования итератор традиционно представляется в виде процедуры. Например, так на языке CLU может быть написано суммирование всех элементов множества s с помощью итератора elements (s) (листинг 4.1).
Листинг 4.1. Пример использования итератора
for i: int in intset$elements(s) do
Итераторы могут быть положены в основу декларативного программирования. Так можно на декларативном языке указать множество жителей города Старый Петергоф:
which (х: х живет в Старом Петергофе)
3.3.5. Оператор исключения
Говорят, что в программе имеет место исключение, когда выполнение программы прерывается из-за возникновения некоторого события. Исключения, как правило, должны обрабатываться программным образом, после чего исполнение программы должно продолжаться дальше. Наиболее важно, чтобы поступление событий обрабатывалось соответствующим образом в системах реального времени (например, в программном обеспечении атомных электростанций или космических кораблей, находящихся в длительном космическом перелете).
Обратим внимание на то, что многие широко распространенные языки программирования (например, Pascal) не имеют механизма обработки прерываний.
Программист может явным образом разрешать или запрещать проверку почти всех условий с помощью явных префиксов, приписываемых к инструкциям, блокам или подпрограммам. Например, в данном случае в блоке будет выполняться проверка на выход индекса за границы массива:
Пример структурного предложения языка «Автокод Эльбрус» выглядит так:
Структурный переход по ситуации c1 в закрытом предложении может быть выполнен, например, следующим образом: c1!.
3.3.6. Зависимости по управлению и по данным
Важную роль при анализе возможности распараллеливания программы играют зависимости по управлению и по данным. Для их анализа может быть построен граф программной зависимости. Его вершинами являются операторы и предикатные выражения, а дуги указывают значения данных, от которых зависят операции, и управляют условиями, от которых зависит выполнение операции.
Пример зависимости по управлению:
/*исполнение этого оператора зависит от c1 */
Множество всех зависимостей задает на операторах и предикатах частичный порядок, которому нужно следовать, чтобы сохранить семантическую целостность программы.
3.4. Абстракция модульности
3.4.1. Модульное программирование
3.4.2. Определения модуля и его примеры
3.4.3. Характеристики модульности
Связность (прочность) модуля
Существует гипотеза о глобальных данных, утверждающая, что глобальные данные вредны и опасны. Идея глобальных данных дискредитирует себя так же, как и идея оператора безусловного перехода goto. Локальность данных дает возможность легко читать и понимать модули, а также легко удалять их из программы.
О средствах задания информационной связности
Обратим внимание на то, что средства для задания информационно прочных модулей отсутствовали в ранних языках программирования (например, FORTRAN и даже в оригинальной версии языка Pascal). И только позже, в языке программирования Ada, появился пакет- средство задания информационно прочного модуля.
И только позже, в языке программирования Ada, появился пакет- средство задания информационно прочного модуля.
Источник
Видео
Что такое уровни абстракции и как их различать?
Про абстракции в программировании и АйТи
Три столпа ООП. Часть IV — Абстракция
Lisp: побеждая посредственность (Пол Грэм)
Шпаргалка 02. Уровни абстракции
ЯЗЫКИ ПРОГРАММИРОВАНИЯ. ЧТО НУЖНО ЗНАТЬ!
Абстракция в ООП
5 лёгких языков программирования, которые интересно учить!
Основы Python #14: уровни абстракции (мини quasi лаба)
😱 САМЫЕ СЛОЖНЫЕ ЯЗЫКИ ПРОГРАММИРОВАНИЯ
Понятие сущности
Понятие сущности. Типы сущностей
Модель «сущность — связь» (или ER-модель) представляет собой способ
логического унифицированного представления данных некоторой предметной области.
Хотя, как мы увидим далее, эта модель
очень напоминает систему связанных друг с другом таблиц, в действительности это
совершенно общее представление. Эта модель может быть преобразована к любой из
существующих конкретных моделей данных: иерархической, сетевой, реляционной,
объектной. Существенно, что ER-модель
позволяет представлять только данные, но не действия, которые с ними могут
производиться, поэтому она используется лишь для проектирования структуры
хранимых данных. Поскольку многие
понятия, которые мы будем разбирать в связи с моделью «сущность — связь»
были нами рассмотрены в основах
реляционных баз данных (параграфы
1.1,1.2,1.3), будем опираться на эти знания.
Эта модель может быть преобразована к любой из
существующих конкретных моделей данных: иерархической, сетевой, реляционной,
объектной. Существенно, что ER-модель
позволяет представлять только данные, но не действия, которые с ними могут
производиться, поэтому она используется лишь для проектирования структуры
хранимых данных. Поскольку многие
понятия, которые мы будем разбирать в связи с моделью «сущность — связь»
были нами рассмотрены в основах
реляционных баз данных (параграфы
1.1,1.2,1.3), будем опираться на эти знания.
Достоинствами данной модели являются
· Простота
· Наглядность.
· Однозначность.
· Использование естественного языка.
Определение
Сущность это собирательное понятие, некоторая
абстракция реально существующего объекта, процесса, явления или некоторого
представления об объекте, информацию о котором требуется хранить в базе данных.
Необходимо различать такие понятия, как тип сущности и экземпляр сущности. Понятие тип сущности относится к набору однородных личностей, предметов, событий или идей, выступающих как целое. Экземпляр сущности относится к конкретной вещи в наборе. Например, типом сущности может быть ГОРОД, а экземпляром – Москва, Киев и т.д. Предполагается, что гарантировано отличие экземпляров одного типа сущности друг от друга. Данное требование вполне аналогично требованию отсутствия в таблице тождественных строк. В дальнейшем, однако, там, где это не может вызвать неоднозначного прочтения, мы не будем различать типы и экземпляры, а будем просто использовать термин «сущность». Принято выражать (именовать) сущность существительным или существительным с характеризующим его прилагательным (СТУДЕНТ, ДЕКАНАТ, ВЫПУСКАЮЩАЯ КАФЕДРА и др.).
Выделяют три вида сущностей: стержневая, ассоциативная
(ассоциация) и характеристическая (характеристика). Кроме этого во множестве ассоциативных сущностей также определяют подмножество обозначений. Дадим теперь определение
видам сущностей.
Кроме этого во множестве ассоциативных сущностей также определяют подмножество обозначений. Дадим теперь определение
видам сущностей.
Стержневая сущность.
Стержневая (сильная) сущность – независящая от других сущность. Стержневая сущность не может быть ассоциацией, характеристикой или обозначением (см. ниже).
Ассоциация.
Ассоциативная сущность (или ассоциация) выражает собой связь «многие ко многим» между двумя сущностями. Является вполне самостоятельной сущностью. Например, между сущностями МУЖЧИНА и ЖЕНЩИНА существует ассоциативная связь, выражаемая ассоциативной сущностью БРАК.
Характеристика.
Характеристическую сущность еще
называют слабой сущностью. Она связана с более сильной сущностью связями «один
ко многим» и «один к одному». Характеристическая сущность описывает или
уточняет другую сущность. Она полностью зависит от нее и исчезает с
исчезновением последней. Например, сущность Зарплата является характеристикой
конкретных работников предприятия и не может в таком контексте существовать
самостоятельно – при удалении экземпляра сущности Работника должны быть удалены
и экземпляры сущности Зарплата, связанные с удаляемым работником.
Обозначение.
Обозначение это такая сущность, с которой другие сущности связаны по принципу «многие к одному» или «один к одному». Обозначение, в отличие характеристики является самостоятельной сущностью. Например, сущность Факультет обозначает принадлежность студента к данному подразделению института, но является вполне самостоятельной.
Любой фрагмент предметной области
может быть представлен некоторым набором сущностей и связями между ними.
Например, рассматривая предметную область ФАКУЛЬТЕТ можно
выделить следующие основные сущности: СТУДЕНТ, КАФЕДРА, СПЕЦИАЛЬНОСТЬ, ДЕКАНАТ, ГРУППА,
ПРЕПОДАВАТЕЛЬ, ЭКЗАМЕН. На
первом этапе создания ER-модели
данных следует выделить все сущности,
которые предполагается описывать исходя из постановки задачи. Лишний раз
подчеркнем, что сущностью может быть не
только некоторый материальный объект, но и некоторый процесс, например ЭКЗАМЕН, ЛЕКЦИЯ.
Сущностью может быть и некоторая количественная и качественные характеристики
объекта: УЧЕНОЕ
ЗВАНИЕ, СТАЖ и др. Все в действительности зависит от постановки
задачи и от нашего анализа предметной области.
Все в действительности зависит от постановки
задачи и от нашего анализа предметной области.
Основные понятия
Рассмотрим другие важные понятия, используемые при построении ER-модели. Мы ввели уже понятие сущности. Остановимся на трех других Понятиях: атрибут сущности, ключ, связь.
Система диаграмм
Следует заметить, что в настоящее время разработано несколько различных графических методов представления диаграмм в модели «сущность — связь». Рассмотрим один из возможных подходов, в основе которого лежат диаграммы Чена.
Таблица 1.6. Обозначения для ER-модели
|
Изображение |
Комментарий |
|
|
Так на диаграмме изображается сильная сущность[1]. |
|
|
Так на диаграмме изображается сущность, отличная от сильной сущности, без уточнения ее типа. |
|
|
Атрибут сущности. Вместо имени атрибута можно указать многоточие «…», что будет обозначать группу атрибутов. |
|
|
Атрибут сущности, являющийся первичным ключом. |
|
|
Обозначает связь, между двумя сущностями. |
|
|
Ассоциативная сущность (связь «многие ко многим»). |
|
|
Обозначение сущности вида «характеристика». |
|
|
Показывает сущность вида «обозначение». |
|
|
Прямая линия указывает на связь между сущностями, либо соединяет сущность и атрибут. Линия со стрелкой указывает направленную связь. |
Правила порождения
И так ER-диаграммы построены. Следующий этап
проектирования – перенести диаграммы на язык таблиц конкретной СУБД. Можно
сказать, что ER-диаграммы
порождают реляционную базу данных. Оказывается процесс порождения можно легко
формализовать, довести до автоматизма. Прежде всего, заметим, что почти всегда есть взаимнооднозначное
соответствие между сущностью и таблицей. При этом атрибуты сущности переходят в
атрибуты (столбцы) таблицы, а первичный ключ сущности переходит
в первичный ключ таблицы. В Таблице 1.7 представлены правила
соответствия бинарных связей сущностей и соответствующих элементов реляционной
базы данных.
Прежде всего, заметим, что почти всегда есть взаимнооднозначное
соответствие между сущностью и таблицей. При этом атрибуты сущности переходят в
атрибуты (столбцы) таблицы, а первичный ключ сущности переходит
в первичный ключ таблицы. В Таблице 1.7 представлены правила
соответствия бинарных связей сущностей и соответствующих элементов реляционной
базы данных.
Таблица 1.7.Правила соответствия
|
Тип бинарной связи |
Элементы реляционной базы данных |
|
Связь «один к одному», характеристики (0,1) — (1,1) (1,1) — (0,1) |
Для каждой сущности строится своя таблица. Связь между таблицами «один к одному». |
|
Связь «один к одному», характеристики (1,1) – (1,1) |
Строится
одна таблица, структура которой состоит из атрибутов обеих сущностей. |
|
Связь «один к одному», характеристики (0,1) – (0,1) |
При построении связи на основе двух таблиц мы вынуждены допустить, что значение внешнего ключа может быть равно NULL. Если исключить эту возможность, то такую связь следует строить на основе трех таблиц. Одна таблица является таблицей – посредником. Она содержит первичные ключи двух других таблиц. |
|
Связь «один ко многим», характеристики (0,1) – (1,N) (1,1) – (1,N)
|
Каждой
сущности ставится в соответствие
таблица. Связи между таблицами имеет тип «один ко многим» и строится
на основе первичного ключа первой таблицы. |
|
Связь «один ко многим», характеристики (0,1) – (0,N) (1,1) – (0,N)
|
Обычно такой тип связи строится на основе трех таблиц (пар. 2, Один ко многим). Таблица посредник содержит внешний ключ, соответствующий первичному ключу первой таблицы и внешний ключ, соответствующий первичному ключу второй таблицы. |
|
Связь «многие ко многим», характеристики (0,N) – (0,N) (1,N) – (1,N) (1,N) – (0,N) (0,N) – (1,N) |
Любая связь такого типа строится на основе трех таблиц (см. пар. 2, Многие ко многим). |
Правила порождения позволят легко
перейти от логической модели данных к физической модели.
Заканчивая рассматривать ER-модель, заметим, что при тщательном анализе предметной области, на предмет выявления сущностей, при переходе к реляционной базе данных дополнительная нормализация таблиц, скорее всего не понадобится. Зависимости внутри таблицы часто означают, что мы в одной таблице пытаемся вместить несколько сущностей.
Функциональные диаграммы
Функциональное моделирование основывается на техниках SADT и IDEF. SADT была предложена Дугласом Россом в середине 1960-х годов. Военно-воздушные силы США использовали методику SADT в своей программе ICAM (Integrated Computer Aided Manufacturing – интеграция компьютерных и промышленных технологий) и назвали ее IDEF В рамках технологии SADT было разработано несколько графических языков моделирования:
■
IDEF0
– для документирования процессов производства и отображения информации об использовании
ресурсов на каждом из этапов проектирования систем.
■ IDEF1 – для документирования информации о производственном окружении систем.
■ IDEF2 – для отображения поведения систем во времени.
■ IDEF3 – для моделирования бизнес процессов.
■ IDEF4 – объектно-ориентированное моделирование.
■ IDEF5 – моделирование наиболее общих (онтологических) закономерностей системы.
Методология IDEF-SADT представляет собой совокупность методов, правил и процедур,
предназначенных для построения функциональной модели какой-либо предметной области. Центральным
понятием этой методологии является
понятие функции. Иногда
используют и другие термины: деятельность или процесс. Под функцией понимается
некоторое действие или набор действий, которые имеют определенную цель и
приводят к конкретным результатам. Определенная функция на диаграмме
обозначается прямоугольником. На диаграмме используются также стрелки, которые
обеспечивают связь между различными функциями (обеспечивают интерфейсы),
связывая их в конечном итоге в единую
систему, моделирующую предметную область. В диаграммах используются стрелки четырех видов, их называют
интерфейсными дугами:
В диаграммах используются стрелки четырех видов, их называют
интерфейсными дугами:
■ I (Input) – вход, т.е. все что является исходным материалом для данной функции. Стрелка входит слева в прямоугольник, обозначающий данную деятельность.
■ O (Output) – результат выполнения функции. Стрелка выходит справа из прямоугольника, обозначающего функцию.
■ C (Control) – ограничения данной функции (все, что ограничивает функцию). Стрелка входит в прямоугольник сверху.
■ M (Mechanism) – механизм, используемый в данной функции. Стрелка входит снизу в прямоугольник — функцию.
На Рис. 1.15 представлен общий вид фрагмента диаграммы, изображенной по методологии SADT.
Рис. 1.15. Общий вид функциональной диаграммы
Рис. 1.18. Диаграмма SADT, полученная из общей диаграммы (см. Рис. 1.17) посредством детализации
Как видно, в частности, на
диаграмме (Рис. 1.18), функции связываются друг с другом при помощи
интерфейсных дуг. Вообще в технологии SADT выделяют семь видов связывания:
1.18), функции связываются друг с другом при помощи
интерфейсных дуг. Вообще в технологии SADT выделяют семь видов связывания:
■ Случайная связность.
■ Логическая связность. Обусловлена тем, что функции или данные относятся к одному классу.
■ Временная связность. Такой тип связности возникает, когда функции выполняются параллельно в одно и тоже время.
■ Процедурная связность. Тип связности возникает, когда функции выполняются в одной и той же части процесса.
■ Коммуникационная связность. Возникает, когда блоки (функции) используют одни и те же данные.
■ Последовательная связность. Возникает, когда выход (выходная дуга) одной функции является одновременно входными данными для другой функции.
■
Функциональная связность. Связность возникает,
когда одна функция воздействует на другую через интерфейсные дуги управления
(на Рис.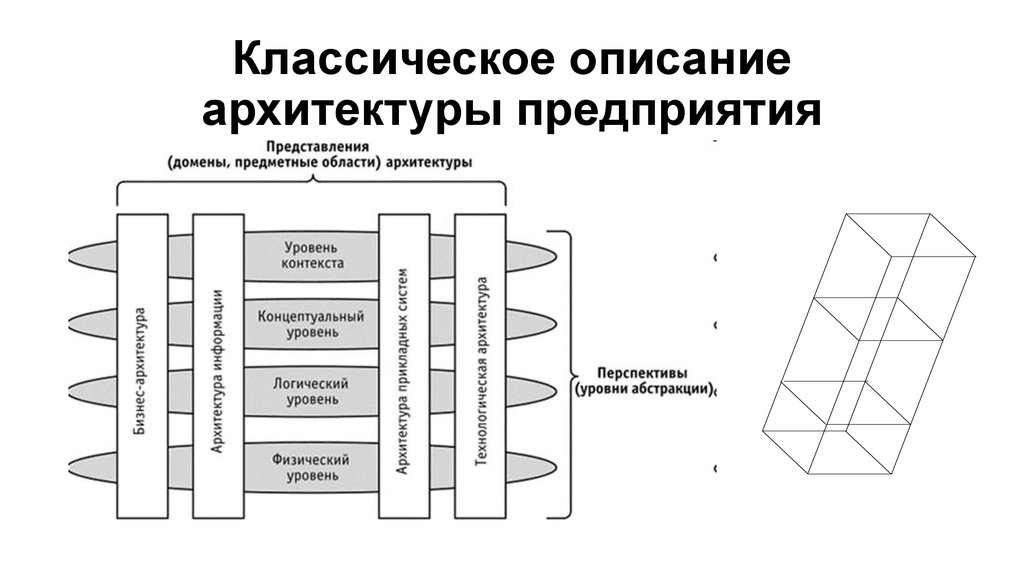 1.18 блок 1 воздействует на
остальные блоки как раз через дуги управления).
1.18 блок 1 воздействует на
остальные блоки как раз через дуги управления).
Диаграммы потоков данных
В основе данной методологии лежит метод диаграмм потоков данных (DFD — Data Flow Diagram). Данные диаграммы призваны описывать процессы преобразования информации от ее ввода в систему до выдачи пользователю. Как и для диаграмм SADT здесь мы также имеем дело с целой иерархией диаграмм, в которой диаграммы нижнего уровня детализируют диаграммы верхнего уровня. Диаграммы верхнего уровня определяют основные процессы и подсистемы информационной системы с внешними входами и выходами. Далее путем декомпозиции диаграммы детализируются. В результате возникает иерархия диаграмм, на самом нижнем уровне которой описаны элементарные процессы. Основными компонентами диаграмм DFD являются:
■ Внешние сущности.
■ Системы и подсистемы.
■ Процессы.
■
Накопители данных.
■ Потоки данных.
Рис. 1.19. Внешняя сущность в потоковых диаграммах
Внешняя сущность представляет собой физическое лицо или предмет являющийся источником или приемником информации. Объект, который мы обозначаем как внешняя сущность, является внешним по отношению к анализируемой предметной области и анализу не подвергается. Это может быть клиент какой-либо службы (если анализируется вся службы) и оператор, работающий с информационной системой (если анализу подвергается только функционирование ИС). Внешняя сущность обознается квадратом (см. Рис. 1.19), несколько приподнятым над плоскостью диаграммы.
Рис. 1.20. Обозначение подсистемы в потоковой диаграмме
На самом верхнем уровне
анализируемая предметная область может быть представлена как некоторая система.
В свою очередь система может быть представлена как совокупность (декомпозиция)
нескольких подсистем. Каждая подсистема получает свой номер. На диаграмме она изображается в виде
прямоугольника с округленными углами (см.
Рис. 1.20). Здесь же указывается номер подсистемы, имя подсистемы в виде
развернутого предложения и имя
проектировщика данной подсистемы.
На диаграмме она изображается в виде
прямоугольника с округленными углами (см.
Рис. 1.20). Здесь же указывается номер подсистемы, имя подсистемы в виде
развернутого предложения и имя
проектировщика данной подсистемы.
Рис. 1.21. Обозначение процесса в потоковой диаграмме
Процесс в модели DFD представляет собой некоторое преобразование входного потока данных в выходной. Под процессом можно понимать и оператора ЭВМ и программу, и работу целого отдела. На диаграмме процесс изображается как подсистема в виде прямоугольника (см. Рис. 1.21). Номер процесса является его идентификатором и состоит из номера процесса или подсистемы верхнего уровня и собственно номера процесса. Имя процесса должно содержать глагол в неопределенной форме и четко определять, что данный процесс делает. Наконец в имени процесса должен быть обозначен объект, который и реализует данный процесс.
Рис. 1.22. Накопитель в потоковой диаграмме
Под накопителем понимается
некоторое устройство, используемое для хранения информации. Способы помещения и
извлечения данных из накопителя могут самые разные. Накопитель данных на
диаграмме изображается в виде прямоугольника (см. Рис. 1.22), разделенного на два отсека. В первом отсеке должен
стоять номер накопителя, начинающийся с буквы D, во втором его имя. Имя накопителя
должно быть достаточно информативным для
использования его в дальнейших разработках. Разумеется при разработке
информационной системы в конечном итоге под накопителем, понимается конкретная
база данных.
Способы помещения и
извлечения данных из накопителя могут самые разные. Накопитель данных на
диаграмме изображается в виде прямоугольника (см. Рис. 1.22), разделенного на два отсека. В первом отсеке должен
стоять номер накопителя, начинающийся с буквы D, во втором его имя. Имя накопителя
должно быть достаточно информативным для
использования его в дальнейших разработках. Разумеется при разработке
информационной системы в конечном итоге под накопителем, понимается конкретная
база данных.
Кроме перечисленных элементов в диаграммах DFD имеются также потоки данных, которые определяют информацию, передаваемую от источника к приемнику. Поток данных на диаграммах изображается линией, заканчивающейся стрелкой. Стрелка указывает на направление передачи информации. Кроме этого для каждого потока должно быть указано имя, которое должно определять его содержание.
Рис. 1.23. Пример потоковой диаграммы, описывающей некоторые процессы подсистемы «Абонент»
UML диаграммы
Как и другие языки моделирования сложных систем, язык UML зиждется на трех принципах:
■
Абстрагирование – отбрасывание тех элементов
системы, которые не существенны с точки зрения рассматриваемой модели.
■ Многомодельность – любая достаточно сложная система не может быть полностью описана только одной моделью.
■ Иерархичность – при описании данной системы используются различные уровни абстрагирования и детализации. На самой вершине иерархии расположена модель, представляющая систему в наиболее полном виде.
Всего в языке UML существует одиннадцать типов диаграмм. Каждая из диаграмм призвана конкретизировать различные представления о рассматриваемой системе. Перечислим типы диаграмм:
■ Диаграммы вариантов использования.
■ Диаграммы классов.
■ Диаграммы поведения.
■ Диаграммы состояний.
■ Диаграммы деятельности.
■ Диаграммы взаимодействия.
■ Диаграммы последовательности.
■ Диаграммы кооперации.
■ Диаграммы реализации.
■
Диаграммы компонентов.
■ Диаграммы развертывания.
Остановимся только на одном типе диаграммы – диаграмме классов, который непосредственно можно применить при разработке структуры баз данных. Данный вид диаграмм должен содержать набор классов, анализируемой предметной области, связи между ними, а также возможные ограничения и комментарии.
Классом в языке UML будем называть именованное описание множества однородных объектов, имеющие одинаковые атрибуты, операции, отношения с другими объектами и семантику.
Атрибут класса — именованное свойство класса, описывающее множество значений, которые принимают экземпляры этого свойства.
Операцией класса будем называть именованную услугу, которую можно запросить у любого экземпляра данного класса.
Между классами в диаграмме могут существовать связи трех типов: зависимости, обобщения и ассоциации.
Определение зависимости.
Связь между двумя классами называю зависимостью, если изменение в спецификации одного класса может повлиять на поведение другого класса.
Определение обобщения.
Обобщением называется связь между классами, когда один из классов является частным случаем второго.
Общий класс при наследовании называется родителем, предком или суперклассом, а частный класс – потомком. Например, при анализе такой системы как школа, можно выделить суперкласс Человек, в который будут входить такие классы – потомки, как учителя, административные работники школы, ученики, родители учеников. В дальнейшем класс учителей можно рассматривать как суперкласс по отношению к обычным учителям и классным руководителям.
Определение ассоциации.
Ассоциация показывает, что между объектами одного класса существует
некоторая связь с объектами другого класса. Допускается, что класс может быть связан
сам с собой. Кроме этого в связи могут участвовать более двух классов.
Ассоциативная связь может характеристики:
■ Имя связи.
■ Роли связи. Для каждого класса, участвующего в ассоциативной связи могут быть указаны роли. Например, для связи между классами Учителя и Ученики можно указать роли: обучающий и обучаемый.
■ Кратность связи. Кратность определяет, сколько объектов данного класса может или должно участвовать в данной связи. Например, кратность 0..1 говорит, что не все экземпляры класса могут участвовать в данной связи, но в каждом экземпляре связи может участвовать только один объект класса.
■
Агрегация.
Если в ассоциативной связи один из классов выступает в роли «целого», а второй
в роли «части целого», то такой типа
связь называется агрегатной связью. В ней один из классов играет главную, а
другой (другие) подчиненную роль. Сильная агрегатная связь называется композицией. При такой связи уничтожении главного класса
приводит к уничтожению подчиненного класса.
При такой связи уничтожении главного класса
приводит к уничтожению подчиненного класса.
В диаграммах классов могут также указываться ограничения, которые затем должны поддерживаться в базах данных. Ограничения могут выражаться предложениями на естественном языке, но могут записываться на специальном языке OCL (Object Constraint Language – язык объектных ограничений). Язык OCL является подмножеством языка UML. Это формальный язык, который позволяет выразить логику ограничений, накладываемых на отдельные элементы диаграмм.
Рис. 1.24. пример простейшей UML-диаграммы
На Рис. 1.24 представлена простейшая UML-диаграмма, на которой изображено три
класса: Студенты, Оценки, Предметы. Связь между всеми тремя между всеми тремя
классами носит ассоциативную природу. Обратите внимание на значок. Он означает,
что налицо агрегатной связи – оценка ставится конкретному студенту и
неотъемлемо принадлежит ему. Более того,
данный тип агрегации, несомненно, является композитной (закрашенный ромб), так
как оценки не могут существовать без конкретного студента. У каждой связи указывается его имя, но роли
связи я не указываю, так в данном случае это не добавляет ясности в диаграмму,
а скорее затруднит ее чтение. Обратим
внимание, что у каждого класса указываются не только атрибуты, но операции (или
методы). Разумеется, диаграмма может не
вместить все атрибуты и операции.
У каждой связи указывается его имя, но роли
связи я не указываю, так в данном случае это не добавляет ясности в диаграмму,
а скорее затруднит ее чтение. Обратим
внимание, что у каждого класса указываются не только атрибуты, но операции (или
методы). Разумеется, диаграмма может не
вместить все атрибуты и операции.
2.7 Абстракция объекта
c⚬mp⚬петь программы
- Текст
- Проекты
- Репетитор
- О
Глава 2Скрыть содержание
2.1 Введение
2.2 Абстракция данных
2.3 Последовательности
 3.3 Обработка последовательности
3.3 Обработка последовательности2.4 Изменяемые данные
2.5 Объектно-ориентированное программирование
2.6 Реализация классов и объектов
 6.1 Экземпляры
6.1 Экземпляры2.7 Абстракция объекта
2.8 Эффективность
2.9 Рекурсивные объекты
Система объектов позволяет программистам создавать и использовать абстрактные данные представления эффективно. Он также предназначен для нескольких представления абстрактных данных сосуществуют в одной и той же программе.
Центральным понятием абстракции объектов является общая функция , которая является
функция, которая может принимать значения нескольких разных типов. мы рассмотрим
три разных метода реализации универсальных функций: общий
интерфейсы, диспетчеризация типов и приведение типов. В процессе построения
эти концепции, мы также обнаружим особенности объектной системы Python, которые
поддерживать создание универсальных функций.
мы рассмотрим
три разных метода реализации универсальных функций: общий
интерфейсы, диспетчеризация типов и приведение типов. В процессе построения
эти концепции, мы также обнаружим особенности объектной системы Python, которые
поддерживать создание универсальных функций.
2.7.1 Преобразование строк
Для эффективного представления данных значение объекта должно вести себя как данные, которые он должен представлять, включая создание строкового представления сам. Строковые представления значений данных особенно важны в интерактивный язык, такой как Python, который автоматически отображает строку представление значений выражений в интерактивном сеансе.
Строковые значения обеспечивают основное средство для обмена информацией между
люди. Последовательности символов могут отображаться на экране, распечатываться на бумаге,
читать вслух, конвертировать в шрифт Брайля или транслировать как азбуку Морзе. Строки также
имеют фундаментальное значение для программирования, потому что они могут представлять выражения Python.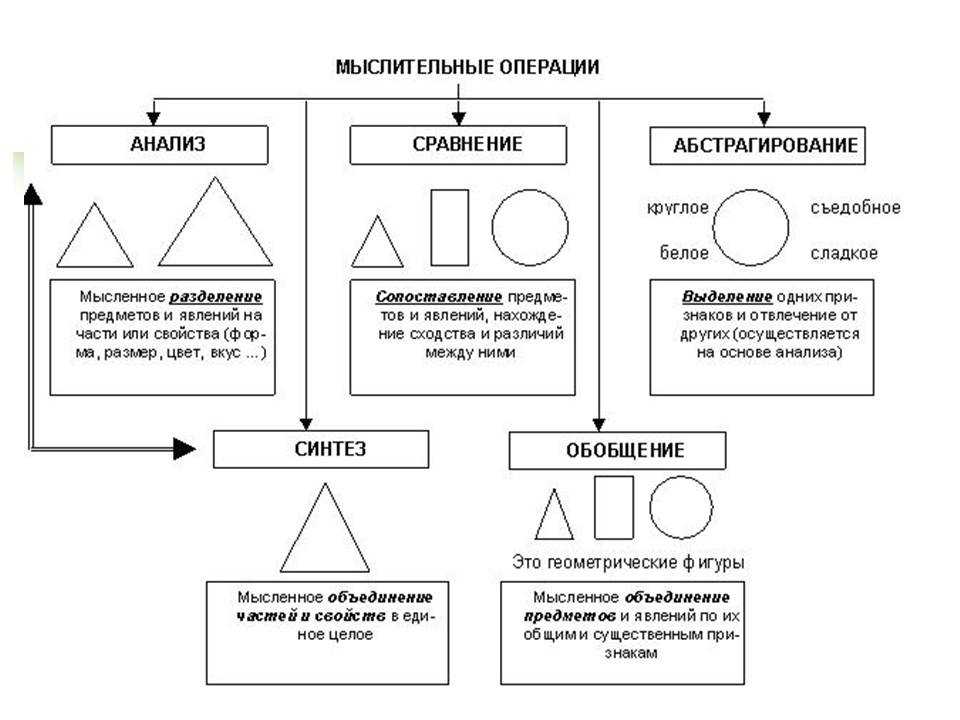
В Python предусмотрено, что все объекты должны создавать две разные строки репрезентации: текст, интерпретируемый человеком, и текст, Python-интерпретируемое выражение. Функция-конструктор для строк, str, возвращает удобочитаемую строку. Где возможно, функция repr возвращает выражение Python, которое оценивается как равный объект. Строка документации для repr объясняет это свойство:
repr(объект) -> строка Возвращает каноническое строковое представление объекта. Для большинства типов объектов eval(repr(object)) == object.
Результатом вызова repr для значения выражения является то, что Python печатает в интерактивном сеансе.
>>> 12e12 12000000000000,0 >>> напечатать (репр (12e12)) 12000000000000,0
В случаях, когда не существует представления, оценивающего исходное значение, Python обычно создает описание, заключенное в угловые скобки.
>>> репр(мин) '<встроенная функция min>'
Конструктор str часто совпадает с repr, но обеспечивает более
интерпретируемое текстовое представление в некоторых случаях. Например, мы видим
разница между str и repr с датами.
Например, мы видим
разница между str и repr с датами.
>>> с даты импорта даты и времени >>> вт = дата(2011, 9, 12) >>> репр(вт) 'datetime.date(2011, 9, 12)' >>> ул(вт) '2011-09-12'
Определение функции repr представляет новую проблему: мы хотели бы, чтобы она корректно применяются ко всем типам данных, даже к тем, которые не существовали при воспроизведении. был реализован. Мы хотели бы, чтобы это была универсальная или полиморфная функция , тот, который может применяться ко многим ( поли ) различным формам ( morph ) данных.
Система объектов предлагает элегантное решение в этом случае: функция всегда вызывает метод с именем __repr__ для своего аргумента.
>>> вт.__репр__() 'datetime.date(2011, 9, 12)'
Реализуя тот же метод в пользовательских классах, мы можем расширить
применимость repr к любому классу, который мы создадим в будущем. Этот пример
подчеркивает еще одно преимущество точечных выражений в целом: они обеспечивают
механизм для расширения области существующих функций на новые типы объектов.
Конструктор str реализован аналогичным образом: он вызывает метод вызвал __str__ для своего аргумента.
>>> вт.__str__() '2011-09-12'
Эти полиморфные функции являются примерами более общего принципа: определенные функции должны применяться к нескольким типам данных. Кроме того, один из способов создания такая функция заключается в использовании общего имени атрибута с другим определением в каждом классе.
2.7.2 Специальные методы
В Python некоторые специальные имена вызываются интерпретатором Python в особые обстоятельства. Например, метод __init__ класса автоматически вызывается всякий раз, когда создается объект. Метод __str__ вызывается автоматически при печати, а __repr__ вызывается в интерактивный сеанс для отображения значений.
В Python есть специальные имена для многих других функций. Некоторые из используемых чаще всего описаны ниже.
Истинные и ложные значения. Ранее мы видели, что числа в Python имеют
истинностное значение; более конкретно, 0 является ложным значением, а все остальные числа
истинные ценности. На самом деле все объекты в Python имеют истинностное значение. По умолчанию,
объекты пользовательских классов считаются истинными, но специальные
Метод __bool__ можно использовать для переопределения этого поведения. Если объект определяет
метод __bool__, то Python вызывает этот метод, чтобы определить его истинность
ценность.
На самом деле все объекты в Python имеют истинностное значение. По умолчанию,
объекты пользовательских классов считаются истинными, но специальные
Метод __bool__ можно использовать для переопределения этого поведения. Если объект определяет
метод __bool__, то Python вызывает этот метод, чтобы определить его истинность
ценность.
В качестве примера предположим, что мы хотим, чтобы банковский счет с нулевым балансом был ложным. Мы можно добавить метод __bool__ в класс Account для создания такого поведения.
>>> Account.__bool__ = lambda self: self.balance != 0
Мы можем вызвать конструктор bool, чтобы увидеть истинное значение объекта, и мы можем использовать любой объект в логическом контексте.
>>> bool(Счет('Джек'))
ЛОЖЬ
>>> если не Аккаунт('Джек'):
print('У Джека ничего нет')
у Джека ничего нет
Последовательность операций. Мы видели, что можем вызвать функцию len для определить длину последовательности.
>>> len('Вперёд, медведи!')
9
Функция len вызывает метод __len__ своего аргумента для определения
его длина.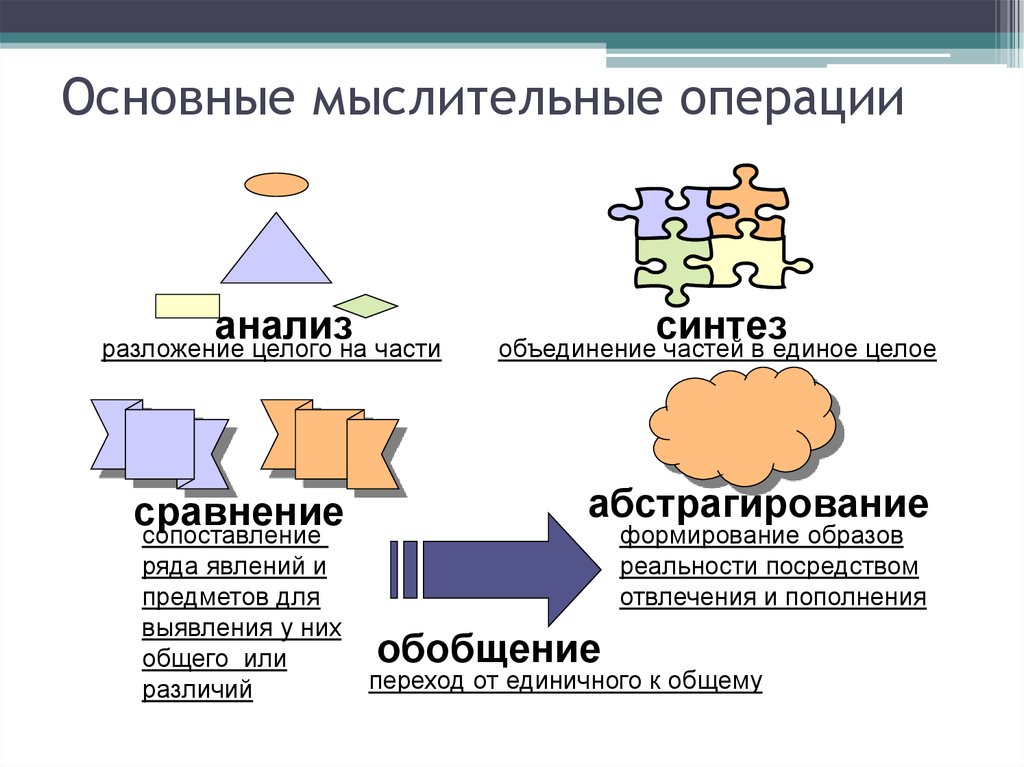 Все встроенные типы последовательностей реализуют этот метод.
Все встроенные типы последовательностей реализуют этот метод.
>>> 'Вперёд, медведи!'.__len__() 9
Python использует длину последовательности для определения ее значения истинности, если это не так. предоставить метод __bool__. Пустые последовательности ложны, а непустые последовательности верны.
>>> логическое значение ('')
ЛОЖЬ
>>> буль([])
ЛОЖЬ
>>> bool('Вперёд, медведи!')
Истинный
Метод __getitem__ вызывается оператором выбора элемента, но он также может быть вызван напрямую.
>>> 'Вперёд, медведи!'[3] 'Б' >>> 'Вперед, медведи!'.__getitem__(3) 'Б'
Вызываемые объекты. В Python функции являются объектами первого класса, поэтому они могут
передаваться как данные и иметь атрибуты, как и любой другой объект. Python также
позволяет нам определять объекты, которые могут быть «вызваны» подобно функциям, путем включения
__вызов__ метода. С помощью этого метода мы можем определить класс, который ведет себя как
функция более высокого порядка.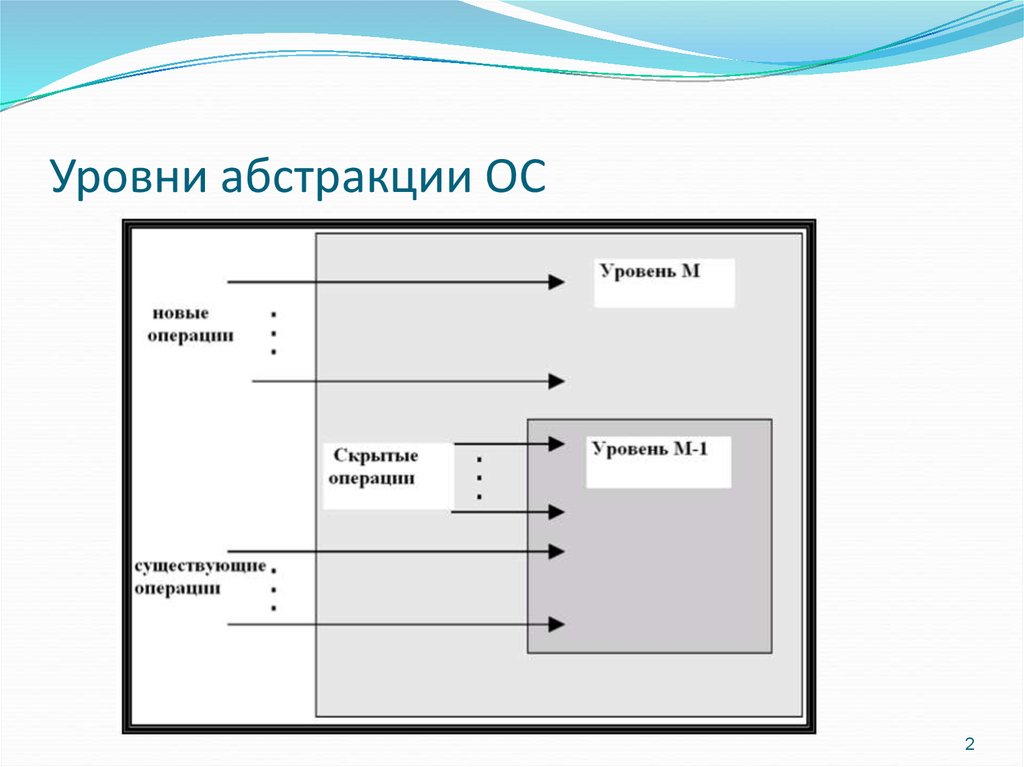
В качестве примера рассмотрим следующую функцию высшего порядка, которая возвращает функция, которая добавляет постоянное значение к своему аргументу.
>>> по умолчанию make_adder(n): определитель сумматора (k): вернуть п + к обратный сумматор
>>> add_three = make_adder(3) >>> add_three(4) 7
Мы можем создать класс Adder, определяющий метод __call__ для предоставления тот же функционал.
>>> класс Adder(объект): защита __init__(я, п): селф.n = n def __call__(я, к): вернуть себя.n + k
>>> add_three_obj = сумматор(3) >>> add_three_obj(4) 7
Здесь класс Adder ведет себя как класс make_adder более высокого порядка. функция, а объект add_three_obj ведет себя как add_three функция. Мы еще больше размыли грань между данными и функциями.
Арифметика. Специальные методы также могут определять поведение встроенных
операторы, применяемые к пользовательским объектам. Чтобы обеспечить эту общность,
Python следует определенным протоколам для применения каждого оператора. Например, чтобы
оценивают выражения, содержащие оператор +, Python проверяет специальные
методы как для левого, так и для правого операнда выражения. Во-первых, Питон
проверяет метод __add__ для значения левого операнда, затем проверяет
для метода __radd__ значения правого операнда. Если это
найден, этот метод вызывается со значением другого операнда в качестве его
аргумент. Некоторые примеры приведены в следующих разделах. Для читателей
заинтересованы в дополнительных деталях, документация Python описывает
исчерпывающий набор имен методов для операторов.
В книге «Погружение в Python 3» есть глава, посвященная именам специальных методов, которые
описывает, сколько из этих имен специальных методов используется.
Например, чтобы
оценивают выражения, содержащие оператор +, Python проверяет специальные
методы как для левого, так и для правого операнда выражения. Во-первых, Питон
проверяет метод __add__ для значения левого операнда, затем проверяет
для метода __radd__ значения правого операнда. Если это
найден, этот метод вызывается со значением другого операнда в качестве его
аргумент. Некоторые примеры приведены в следующих разделах. Для читателей
заинтересованы в дополнительных деталях, документация Python описывает
исчерпывающий набор имен методов для операторов.
В книге «Погружение в Python 3» есть глава, посвященная именам специальных методов, которые
описывает, сколько из этих имен специальных методов используется.
2.7.3 Множественные представления
Барьеры абстракции позволяют нам разделить использование и представление данных.
Однако в больших программах не всегда имеет смысл говорить о
базовое представление» для типа данных в программе. Во-первых, существует
может быть более чем одно полезное представление для объекта данных, и мы могли бы
нравится разрабатывать системы, которые могут иметь дело с несколькими представлениями.
В качестве простого примера комплексные числа могут быть представлены двумя почти эквивалентными способами: в прямоугольной форме (действительная и мнимая части) и в полярной форма (величина и угол). Иногда прямоугольная форма более уместна а иногда полярная форма является более подходящей. Действительно, это совершенно правдоподобно представить себе систему, в которой комплексные числа представлены в обоих способами, и в которых функции для работы с комплексными числами работают с либо представление. Мы реализуем такую систему ниже. В качестве примечания, мы разработка системы, которая выполняет арифметические операции над комплексными числами как простой, но нереалистичный пример программы, использующей общие операции. А тип комплексного числа на самом деле встроенный в Python, но для этого примера мы реализуем свой собственный.
Регулярно возникает идея разрешить множественное представление данных.
Большие программные системы часто разрабатываются многими людьми, работающими в течение длительного времени. периоды времени с учетом требований, которые со временем меняются. В таком
условиях, просто не каждый может заранее договориться о
выбор представления данных. В дополнение к барьерам абстракции данных
которые изолируют представление от использования, нам нужны барьеры абстракции, которые изолируют
различные варианты дизайна друг от друга и позволяют различные варианты для
сосуществовать в одной программе.
периоды времени с учетом требований, которые со временем меняются. В таком
условиях, просто не каждый может заранее договориться о
выбор представления данных. В дополнение к барьерам абстракции данных
которые изолируют представление от использования, нам нужны барьеры абстракции, которые изолируют
различные варианты дизайна друг от друга и позволяют различные варианты для
сосуществовать в одной программе.
Мы начнем нашу реализацию на самом высоком уровне абстракции и будем работать к конкретным представлениям. Комплексное число — это число, и числа можно складывать или перемножать. Как числа могут быть добавлены или multiplied абстрагируется именами методов add и mul.
>>> Номер класса: def __add__(я, другой): вернуть self.add (другое) def __mul__(я, другой): вернуть self.mul(другое)
Этот класс требует, чтобы объекты Number имели методы add и mul, но
не определяет их. Более того, у него нет метода __init__.
цель Number не в том, чтобы создавать экземпляры напрямую, а вместо этого служить
как надкласс различных конкретных числовых классов. Наша следующая задача — определить
add и mul соответственно для комплексных чисел.
Наша следующая задача — определить
add и mul соответственно для комплексных чисел.
Комплексное число можно рассматривать как точку в двумерном пространстве с две ортогональные оси, действительная ось и мнимая ось. Из этого перспектива, комплексное число c = real + imag * i (где i * i = -1) можно рассматривать как точку на плоскости, горизонтальная координата которой равна real и вертикальной координатой которого является imag. Добавление комплексных чисел включает добавление их соответствующих реальных координат и координат изображения.
При умножении комплексных чисел более естественно мыслить в терминах комплексное число в полярной форме, как величина и угол. Произведение двух комплексных чисел — это вектор, полученный растягивая одно комплексное число на коэффициент длины другого, а затем поворачивая его на угол другого.
Класс Complex наследуется от Number и описывает арифметику для комплексные числа.
>>> класс Комплекс(Число): def добавить (я, другой): return ComplexRI(self.real + other.real, self.imag + other.imag) def mul(я, другой): величина = собственная величина * другая.величина return ComplexMA (величина, собственный угол + другой угол)
В этой реализации предполагается, что для комплексных чисел существуют два класса: соответствующие их двум естественным представлениям:
- ComplexRI строит комплексное число из действительной и мнимой частей.
- ComplexMA строит комплексное число из величины и угла.
Интерфейсы. Атрибуты объекта, которые являются формой передачи сообщений, позволяют
разные типы данных, чтобы по-разному реагировать на одно и то же сообщение. А
общий набор сообщений, вызывающих сходное поведение у разных классов, — это
мощный метод абстракции. Интерфейс представляет собой набор общих атрибутов
имена, а также описание их поведения. В случае сложных
числа, интерфейс, необходимый для реализации арифметики, состоит из четырех
атрибуты: действительный, имаг, величина и угол.
Чтобы сложные арифметические операции были правильными, эти атрибуты должны быть согласованы. Что есть прямоугольные координаты (реальные, изображения) и полярные координаты (величина, угол) должны описывать одну и ту же точку на комплексной плоскости. Класс Complex неявно определяет этот интерфейс, определяя, как эти атрибуты используются для сложения и умножения комплексных чисел.
Недвижимость. Требование, чтобы два или более значений атрибута поддерживали фиксированные отношения друг с другом — новая проблема. Одно из решений — хранить значения атрибутов только для одного представления и вычислить другое представительство всякий раз, когда это необходимо.
Python имеет простую функцию для вычисления атрибутов на лету из
функции с нулевым аргументом. Декоратор @property позволяет функциям быть
вызывается без синтаксиса выражения вызова (круглые скобки после выражения).
Класс ComplexRI хранит реальные атрибуты и атрибуты изображений и вычисляет
величина и угол по запросу.
>>> из математического импорта atan2
>>> класс ComplexRI(Комплекс):
def __init__(я, реальный, образ):
самостоятельный = настоящий
self.imag = изображение
@имущество
величина определения (я):
возврат (self.real ** 2 + self.imag ** 2) ** 0,5
@имущество
Угол защиты (я):
вернуть atan2 (self.imag, self.real)
защита __repr__(сам):
return 'ComplexRI({0:g}, {1:g})'.format(self.real, self.imag)
В результате этой реализации все четыре атрибута, необходимые для сложных к арифметике можно получить доступ без каких-либо выражений вызова, и изменения в реальные или изображения отражаются в величине и угле.
>>> ri = Сложный RI(5, 12) >>> ри.реал 5 >>> ri.величина 13,0 >>> ри.реал = 9 >>> ри.реал 9 >>> ri.величина 15,0
Точно так же класс ComplexMA хранит величину и угол, но вычисляет real и imag всякий раз, когда просматриваются эти атрибуты.
>>> из математики импортировать sin, cos, pi >>> класс ComplexMA(Комплекс): def __init__(я, величина, угол): собственная величина = величина собственный угол = угол @имущество определение реальное (я): вернуть self.magnitude * cos(self.angle) @имущество деф образ(я): вернуть self.magnitude * sin(self.angle) защита __repr__(сам): return 'ComplexMA({0:g}, {1:g} * pi)'.format(self.magnitude, self.angle/pi)
Изменения величины или угла немедленно отражаются в реальном и атрибуты изображения.
>>> ma = ComplexMA(2, pi/2) >>> ma.imag 2.0 >>> ма.угол = пи >>> ма.реал -2,0
Наша реализация комплексных чисел завершена. Любой класс реализация комплексных чисел может использоваться для любого аргумента в любом арифметическая функция в комплексе.
>>> из математического импорта пи >>> Комплекс RI(1, 2) + КомплексMA(2, пи/2) Комплекс РИ(1, 4) >>> Комплекс RI(0, 1) * Комплекс RI(0, 1) КомплексMA(1, 1 * пи)
Интерфейсный подход к кодированию нескольких представлений привлекателен.
характеристики. Класс для каждого представления может быть разработан отдельно;
они должны договориться только об именах атрибутов, которые они разделяют, а также о любых
условия поведения для этих атрибутов. Интерфейс тоже добавочный .
Если бы другой программист хотел добавить третье представление комплексных чисел
к той же программе, им нужно будет только создать еще один класс с тем же
атрибуты.
Интерфейс тоже добавочный .
Если бы другой программист хотел добавить третье представление комплексных чисел
к той же программе, им нужно будет только создать еще один класс с тем же
атрибуты.
Множественные представления данных тесно связаны с идеей данных абстракция, с которой мы начали эту главу. Используя абстракцию данных, мы возможность изменить реализацию типа данных без изменения смысла программы. С интерфейсами и передачей сообщений мы можем иметь несколько различные представления в одной и той же программе. В обоих случаях набор имена и соответствующие условия поведения определяют абстракцию, которая позволяет эта гибкость.
2.7.4 Общие функции
Универсальные функции — это методы или функции, которые применяются к аргументам различных
типы. Мы уже видели много примеров. Метод Complex.add
универсальный, потому что он может принимать либо ComplexRI, либо ComplexMA в качестве
значение для др. Эта гибкость была достигнута за счет того, что обе
ComplexRI и ComplexMA имеют общий интерфейс. Использование интерфейсов и
передача сообщений — это только один из нескольких методов, используемых для реализации универсального
функции. В этом разделе мы рассмотрим два других: диспетчеризацию типов и
принуждение типа.
Использование интерфейсов и
передача сообщений — это только один из нескольких методов, используемых для реализации универсального
функции. В этом разделе мы рассмотрим два других: диспетчеризацию типов и
принуждение типа.
Предположим, что в дополнение к нашим классам комплексных чисел мы реализуем Рациональный класс для точного представления дробей. Адд и мул методы выражают те же вычисления, что и методы add_rational и mul_rational функции из ранее в этой главе.
>>> из дробей импорт НОД
>>> класс Rational(Число):
def __init__(я, число, номинал):
g = gcd (число, номинал)
self.numer = число // g
self.denom = номинал // g
защита __repr__(сам):
return 'Rational({0}, {1})'.format(self.numer, self.denom)
def добавить (я, другой):
nx, dx = self.numer, self.denom
ny, dy = др.число, др.деном
return Rational(nx * dy + ny * dx, dx * dy)
def mul(я, другой):
число = собственный.число * другое.число
номинал = собственный.деном * другой.деном
вернуть Rational(число, номинал)
Мы реализовали интерфейс суперкласса Number, включив
методы add и mul. В результате мы можем складывать и умножать рациональные
числа с помощью знакомых операторов.
В результате мы можем складывать и умножать рациональные
числа с помощью знакомых операторов.
>>> Рациональное(2, 5) + Рациональное(1, 10) Рациональный(1, 2) >>> Рациональное(1, 4) * Рациональное(2, 3) Рациональный(1, 6)
Однако мы еще не можем добавить рациональное число к комплексному числу, хотя в математике такое сочетание вполне определено. Мы хотели бы представить это операция перекрестного типа каким-то тщательно контролируемым образом, чтобы мы могли поддерживать это без серьезного нарушения наших барьеров абстракции. Есть напряжение между желаемыми результатами: мы хотели бы иметь возможность добавить сложный числа в рациональное число, и мы хотели бы сделать это, используя общий __add__, который правильно работает со всеми числовыми типами. В В то же время мы хотели бы разделить проблемы комплексных чисел и рациональные числа, когда это возможно, чтобы поддерживать модульную программу.
Тип диспетчерский. Одним из способов реализации операций перекрестного типа является выбор
поведение, основанное на типах аргументов функции или метода. Идея диспетчеризации типов заключается в написании функций, которые проверяют тип.
аргументов, которые они получают, затем выполняют код, подходящий для
эти типы.
Идея диспетчеризации типов заключается в написании функций, которые проверяют тип.
аргументов, которые они получают, затем выполняют код, подходящий для
эти типы.
Встроенная функция isinstance принимает объект и класс. Он возвращается Значение true, если объект имеет класс, который является или наследуется от данного класса.
>>> c = Комплекс RI(1, 1) >>> isinstance(c, ComplexRI) Истинный >>> isinstance(c, Комплекс) Истинный >>> isinstance(c, ComplexMA) ЛОЖЬ
Простым примером диспетчеризации типов является функция is_real, которая использует разные реализации для каждого типа комплексного числа.
>>> определение is_real(c): """Вернуть, является ли c действительным числом без мнимой части.""" если isinstance(c, ComplexRI): вернуть c.imag == 0 elif isinstance(c, ComplexMA): возврат c.angle% пи == 0
>>> is_real (ComplexRI (1, 1)) ЛОЖЬ >>> is_real(ComplexMA(2, pi)) Истинный
Диспетчеризация типов не всегда выполняется с помощью isinstance. Для арифметики
мы дадим атрибут type_tag экземплярам Rational и Complex.
имеет строковое значение. Когда два значения x и y имеют одинаковые
type_tag, то мы можем объединить их напрямую с x.add(y). Если нет, мы
нужна операция перекрестного типа.
Для арифметики
мы дадим атрибут type_tag экземплярам Rational и Complex.
имеет строковое значение. Когда два значения x и y имеют одинаковые
type_tag, то мы можем объединить их напрямую с x.add(y). Если нет, мы
нужна операция перекрестного типа.
>>> Rational.type_tag = 'крыса' >>> Complex.type_tag = 'com' >>> Rational(2, 5).type_tag == Rational(1, 2).type_tag Истинный >>> ComplexRI(1, 1).type_tag == ComplexMA(2, pi/2).type_tag Истинный >>> Rational(2, 5).type_tag == ComplexRI(1, 1).type_tag ЛОЖЬ
Чтобы объединить комплексные и рациональные числа, мы пишем функции, которые полагаются на оба их представлений одновременно. Ниже мы опираемся на то, что Rational можно приблизительно преобразовать в значение с плавающей запятой, которое является реальным количество. Результат можно объединить с комплексным числом.
>>> определение add_complex_and_rational(c, r): return ComplexRI(c.real + r.numer/r.denom, c.imag)
Умножение включает аналогичное преобразование. В полярной форме действительное число в
комплексная плоскость всегда имеет положительную величину. Угол 0 указывает на
положительное число. Угол пи указывает на отрицательное число.
В полярной форме действительное число в
комплексная плоскость всегда имеет положительную величину. Угол 0 указывает на
положительное число. Угол пи указывает на отрицательное число.
>>> def mul_complex_and_rational(c, r): r_величина, r_угол = r.число/r.деном, 0 если r_величина < 0: r_величина, r_угол = -r_величина, пи return ComplexMA(c.величина * r_величина, c.угол + r_угол)
И сложение, и умножение коммутативны, поэтому перестановка аргумента order может использовать одни и те же реализации этих операций перекрестного типа.
>>> определение add_rational_and_complex(r, c): вернуть add_complex_and_rational (c, r)
>>> def mul_rational_and_complex(r, c): вернуть mul_complex_and_rational(c, r)
Роль диспетчеризации типов заключается в обеспечении того, чтобы эти кросс-типные операции
используется в соответствующее время. Ниже мы переписываем суперкласс Number, чтобы использовать
тип диспетчеризации для его методов __add__ и __mul__.
Мы используем атрибут type_tag для различения типов аргументов. Можно было бы напрямую использовать встроенный метод isinstance, но теги упрощают реализация. Использование тегов типов также показывает, что диспетчеризация типов не обязательно связан с объектной системой Python, а вместо этого является общей техникой для создания общих функций в гетерогенных доменах.
Метод __add__ рассматривает два случая. Во-первых, если два аргумента имеют тег того же типа, то предполагается, что метод добавления первого может принимать второй в качестве аргумента. В противном случае он проверяет, есть ли словарь реализации перекрестного типа, называемые сумматорами, содержат функцию, которая может добавлять аргументы этих тегов типа. Если есть такая функция, Метод cross_apply находит и применяет его. Метод __mul__ имеет аналогичная структура.
>>> Номер класса: def __add__(я, другой): если self.type_tag == other.type_tag: вернуть self.add (другое) elif (self.type_tag, other.type_tag) в self.adders: вернуть self.cross_apply (другое, self.adders) def __mul__(я, другой): если self.type_tag == other.type_tag: вернуть self.mul(другое) elif (self.type_tag, other.type_tag) в self.multipliers: вернуть self.cross_apply (другое, self.multipliers) def cross_apply (я, другой, cross_fns): cross_fn = cross_fns[(self.type_tag, other.type_tag)] вернуть cross_fn(я, другой) adders = {("ком", "крыса"): add_complex_and_rational, ("крыса", "com"): add_rational_and_complex} multipliers = {("com", "rat"): mul_complex_and_rational, ("крыса", "ком"): mul_rational_and_complex}
В этом новом определении класса Number все реализации кросс-типа индексируются парами тегов типа в сумматорах и множителях словари.
Этот основанный на словаре подход к диспетчеризации типов является расширяемым. Новый
подклассы Number могли установить себя в систему, объявив
тег типа и добавление операций перекрестного типа в Number.adders и
Числовые множители. Они также могут определять свои собственные сумматоры и
множители в подклассе.
Хотя мы немного усложнили систему, теперь мы можем смешивать типы выражения сложения и умножения.
>>> Сложный RI(1.5, 0) + Рациональный(3, 2) КомплексRI(3, 0) >>> Рациональный(-1, 2) * КомплексныйMA(4, пи/2) КомплексMA(2, 1,5 * пи)
Принуждение. В общей ситуации совершенно не связанных между собой операций действующих
на совершенно несвязанных типах, реализуя явные операции кросс-типа,
каким бы громоздким он ни был, это лучшее, на что можно надеяться. К счастью, мы
иногда может добиться большего успеха, используя дополнительную структуру, которая может быть
скрыто в нашей системе типов. Часто разные типы данных не полностью
независимы, и могут быть способы, которыми можно рассматривать объекты одного типа.
как принадлежащий к другому типу. Этот процесс называется принуждение . Например, если мы
просят арифметически объединить рациональное число с комплексным числом, мы
можно рассматривать рациональное число как комплексное число, мнимая часть которого равна
нуль. После этого мы можем использовать Complex.add и Complex.mul для объединения
их.
После этого мы можем использовать Complex.add и Complex.mul для объединения
их.
В общем, мы можем реализовать эту идею, разработав функции принуждения, которые преобразовать объект одного типа в эквивалентный объект другого типа. Здесь типичная функция принуждения, которая преобразует рациональное число в комплексное число с нулевой мнимой частью:
>>> определение рационального_в_комплексе(г): return ComplexRI(r.число/r.деном, 0)
Альтернативное определение класса Number выполняет кросс-тип операции, пытаясь привести оба аргумента к одному и тому же типу. Словарь приведения индексирует все возможные приведения парой типов теги, указывающие, что соответствующее значение приводит к значению первого типа к значению второго типа.
Как правило, невозможно принудить произвольный объект данных каждого типа
во все остальные виды. Например, нет возможности заставить произвольный
комплексное число в рациональное число, поэтому такого преобразования не будет
реализация в словаре приведения.
Метод принуждения возвращает два значения с одинаковым тегом типа. Он проверяет теги типов своих аргументов, сравнивает их с записями в приведениях словарь и преобразует один аргумент в тип другого, используя принуждать_к. Только одна запись в приведениях необходима для завершения нашего арифметическая система перекрестного типа, заменяющая четыре функции перекрестного типа в тип-диспетчерская версия Number.
>>> Номер класса:
def __add__(я, другой):
х, у = self.coerce (другое)
вернуть х.добавить(у)
def __mul__(я, другой):
х, у = self.coerce (другое)
вернуть x.mul(y)
def coerce (я, другой):
если self.type_tag == other.type_tag:
вернуть себя, другого
elif (self.type_tag, other.type_tag) в self.coercions:
возврат (self.coerce_to(other.type_tag), другое)
elif (other.type_tag, self.type_tag) в self.coercions:
вернуть (я, другое.coerce_to(self.type_tag))
def coerce_to(self, other_tag):
coercion_fn = self.coercions[(self.type_tag, other_tag)]
вернуть coercion_fn (я)
принуждения = {('крыса', 'com'): рациональное_в_комплексное}
Эта схема принуждения имеет некоторые преимущества по сравнению с методом явного определения
операции перекрестного типа. Хотя нам еще нужно написать функции принуждения к
связать типы, нам нужно написать только одну функцию для каждой пары типов
а не разные функции для каждого набора типов и каждого универсального
операция. На что мы рассчитываем здесь, так это на то, что соответствующее
преобразование между типами зависит только от самих типов, а не от
применяется конкретная операция.
Хотя нам еще нужно написать функции принуждения к
связать типы, нам нужно написать только одну функцию для каждой пары типов
а не разные функции для каждого набора типов и каждого универсального
операция. На что мы рассчитываем здесь, так это на то, что соответствующее
преобразование между типами зависит только от самих типов, а не от
применяется конкретная операция.
Дальнейшие преимущества связаны с расширением принуждения. Некоторые более изощренные
схемы принуждения не просто пытаются принудить один тип к другому, но вместо этого
может попытаться привести два разных типа к третьему общему типу. Рассмотреть возможность
ромб и прямоугольник: ни один из них не является частным случаем другого, но оба могут
рассматривать как четырехугольники. Еще одно расширение принуждения — итеративное.
принуждение, при котором один тип данных преобразуется в другой через промежуточный
типы. Учтите, что целое число может быть преобразовано в действительное число сначала
преобразование его в рациональное число, а затем преобразование этого рационального числа в
реальное число.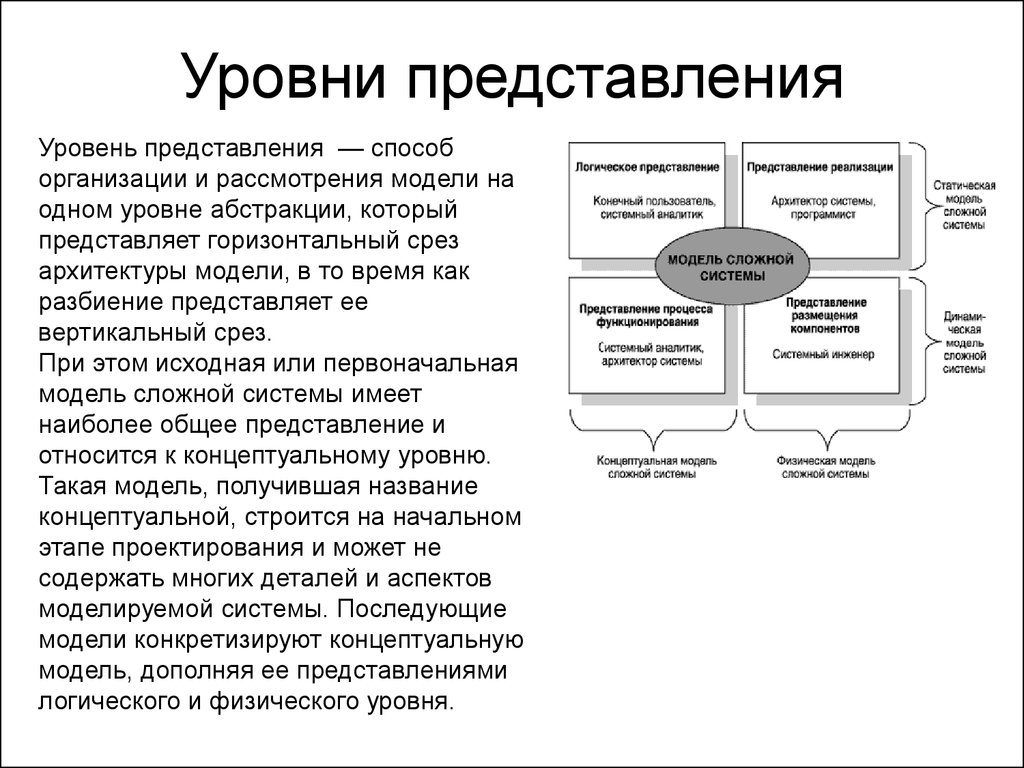 Цепное принуждение таким образом может уменьшить общее количество
функции принуждения, которые требуются программе.
Цепное принуждение таким образом может уменьшить общее количество
функции принуждения, которые требуются программе.
Несмотря на свои преимущества, у принуждения есть потенциальные недостатки. Для одного, функции принуждения могут потерять информацию при их применении. В нашем примере рациональные числа являются точными представлениями, но становятся приближенными, когда они преобразуются в комплексные числа.
Некоторые языки программирования имеют встроенные автоматические системы принуждения. в ранних версиях Python был специальный метод __coerce__ для объектов. В конце концов, сложность встроенной системы принуждения не оправдала его использовать, и поэтому он был удален. Вместо этого определенные операторы применяют принуждение к свои аргументы по мере необходимости.
Продолжить : 2.8 Эффективность
Составление программ Джона Де Неро на основе учебника «Структура и Интерпретация компьютерных программ Гарольда Абельсона и Джеральд Джей Суссман, имеет лицензию Creative Неперенесенная лицензия Commons Attribution-ShareAlike 3. 0.
0.уровней абстракции, ключевая концепция проектирования систем | Дэниел Джин Ю
Работа со сложными системами означает создание различных интерпретаций реальности.
Если вы видели Матрица , вы, возможно, помните эту сцену, где Морфеус сообщает Нео новость о том, что мир, который он считал «реальным», на самом деле является абстракцией — Матрицей.
«Подождите, это просто более высокий уровень абстракции?»НЕО: Это, это ненастоящее?
МОРФЕУС: Что реально? Как определить настоящее? Если вы говорите о том, что вы можете чувствовать, обонять, ощущать на вкус и видеть, то реальность — это просто электрические сигналы, интерпретируемые вашим мозгом. Это мир, который вы знаете. Мир, каким он был в конце ХХ века. Сейчас он существует только как часть нейронно-интерактивной симуляции, которую мы называем Матрица. Ты жил в мире грез, Нео.
Реальность согласно Морфеусу
Морфеус, по сути, говорит, что реальность представляет собой сложную систему, и ее нельзя понять или определить каким-то одним конкретным способом. Реальность лучше понимать как уровни абстракции:
Уровень 2: Человеческое восприятие
На этом более высоком уровне абстракции мы воспринимаем реальность через наши пять человеческих чувств: зрение, слух, осязание, вкус и обоняние. На этом уровне Матрица и Реальность неразличимы.
Этот стул «настоящий», потому что мы можем ощутить его с помощью пяти органов чувств.Уровень 1: наука о мозге
На этом более низком уровне абстракции различные комбинации электрических сигналов интерпретируются мозгом как наши пять чувств. Только на этом более низком уровне абстракции мы можем видеть, что то, что мы считали реальностью, манипулируется с помощью высокотехнологичных стоматологических кресел, которые подключаются непосредственно к мозгу.
Хорошо, давайте выйдем из мира научной фантастики и поищем уровни абстракции в окружающем нас реальном мире. Оказывается, уровни абстракции есть везде, но их трудно увидеть, потому что мы воспринимаем их как должное. Они прячутся на виду.
Пример из жизни: Где вы живете?Представьте, что вы встречаете кого-то нового, и они спрашивают вас: «Где вы живете?» Как бы вы ответили?
- Если вас спросит IRS или заполнит правительственную форму, вы должны указать свой точный почтовый адрес — иначе!
- Если вы встретили кого-то на местном мероприятии или в школе, вы можете ответить: Я живу в голубом доме на Бонд-стрит.
- Но что, если вы посещаете другую страну? Скорее всего, вы скажете: , я живу в США.
- Если бы у вас была внеземная встреча, вы могли бы сказать: Я с планеты Земля.

Это все очень разные ответы! Какой из них настоящий ответ ? Все они, конечно.
Вы бессознательно использовали уровни абстракции. Вы ответили на уровне детализации, который был бы более полезным и описательным для человека, с которым вы разговаривали. Другими словами, вы выбирали уровень абстракции, который наилучшим образом соответствовал цели разговора.
Создание уровней абстракции
Мы можем дать имена этим различным уровням абстракции — более низкие уровни абстракции более специфичны, а более высокие уровни абстракции — более общие.
7. Планетарный — Я с планеты Земля. Отведи меня к своему лидеру.
6. Страна — Я из США .
5. Штат — Я родом из Висконсина .
4. Город — Я живу в Чикаго, Иллинойс .
3. Район — Я живу в Джексон-Хайтс, Квинс
2. Здание — Я живу в синем жилом комплексе на Мичиган-авеню
1. Фактический адрес — 476 N Bond St., Фресно, Калифорния 94420 .
Фактический адрес — 476 N Bond St., Фресно, Калифорния 94420 .
Вы найдете множество различных определений и объяснений слова «абстракция», но я считаю определение из Википедии наиболее полезным при работе со сложными системами,
Абстракции создаются путем выбора только тех аспектов сложной системы, которые релевантны для конкретной субъективно оцениваемой цели.
Последствия определения для проектирования систем
- Абстракции создаются для определенной цели — это инструменты решения проблем, которые мы создаем для конкретной проблемы, задачи или цели.
- Все абстракции являются упрощениями — мы выбираем некоторые аспекты сложной системы и намеренно опускаем другие.
- Абстракции полезны (или нет) — вместо того, чтобы быть хорошими/плохими или правильными/неправильными, абстракции более/менее полезны для решения проблем.
Знаменитая трубка. Как люди упрекали меня за это! И все же, не могли бы вы набить мою трубку? Нет, это просто представление, не так ли? Так что, если бы я написал на своей картинке «Это трубка», я бы солгал!
Как люди упрекали меня за это! И все же, не могли бы вы набить мою трубку? Нет, это просто представление, не так ли? Так что, если бы я написал на своей картинке «Это трубка», я бы солгал!
— Рене Магритт
Должен любить сюрреалистов и их деспотичное послание о том, что искусство и реальность разные — искусство — это абстракция реальности.
Существует много уровней абстракции, чтобы понять, как работает компьютерная программа.Абстракция — широко используемая концепция в компьютерном программировании. Уровней абстракции в этом мультфильме:
99. Исходный код
98. Объектный код
97. Машинный код
96. CPU
95. Микропроцессор
…
36. Кремниевая химия
…
6. Квант -механики
.
ГЛАВА 10
ГЛАВА 10
ПОНЯТИЕ АБСТРАКЦИИ
Абстракция
позволяет собирать экземпляры сущностей в группы, в которых их общие
атрибуты учитывать не нужно.
Два виды абстракций в языках программирования — это абстракция процессов и данных. абстракция.
концепция абстракции процесса один из старейших. Все подпрограммы абстракции процесса, потому что они предоставляют программе способ указать, что какой-то процесс должен быть выполнен, без предоставления подробностей о том, как это должно быть Выполнено.
Процесс абстракция имеет решающее значение для процесса программирования. Возможность абстрагироваться от многих деталей алгоритмов в подпрограмм позволяет создавать, читать и понимать большие программы.
Все подпрограммы, включая параллельные подпрограммы и обработчики исключений, абстракции процессов
ИНКАПСУЛЯЦИЯ
Инкапсуляция — это группа подпрограмм и данных, которыми они манипулируют
Ан инкапсуляция обеспечивает абстрактную систему и логическую организацию для набор связанных вычислений
Они
часто помещаются в библиотеки и становятся доступными для повторного использования в других программах. чем те, для которых они написаны
чем те, для которых они написаны
ВВЕДЕНИЕ К АБСТРАКЦИИ ДАННЫХ
Ан абстрактный тип данных — это просто инкапсуляция, включающая только данные представление одного конкретного типа данных и подпрограмм, обеспечивающих операции для этого типа
Ан экземпляр абстрактного типа данных называется объектом
Объектно-ориентированный программирование является результатом использования абстракции данных КАК РЕЗЮМЕ ТИП ДАННЫХ
Все встроенные типы являются абстрактными типами данных, даже в FORTRAN I
Плавающая точка Типы используют ключевую концепцию абстракции данных: сокрытие информации. Фактический формат данных в ячейка с плавающей запятой скрыта от пользователя.
ПОЛЬЗОВАТЕЛЬ ОПРЕДЕЛЕННЫЕ ТИПЫ ДАННЫХ РЕЗЮМЕ
концепция определяемых пользователем абстрактных типов данных появилась относительно недавно
Они необходимо предоставить:
- А определение типа, которое позволяет программным модулям объявлять переменные типа, но скрывает представление этих переменных
- А набор операций по работе с объектами типа
Ан абстрактный тип данных — это тип данных, который удовлетворяет двум условиям
— представление или определение типа и операции содержатся в единая синтаксическая единица
- представление объектов типа скрыто от модулей программы, использующих тип, так что только прямые операции, возможные на этих объектах, являются теми, предоставлено в определении типов
Программа
единицы, использующие определенный абстрактный тип данных, называются клиентами этого
тип.
А Преимуществом сокрытия информации является повышенная надежность. Это связано с тем, что клиенты не могут изменить лежащие в основе представления объектов напрямую, либо намеренно, либо посредством авария, что повысит целостность объекта
КОНСТРУКЦИЯ ВОПРОСЫ
А средство для определения абстрактных типов данных в языке должно обеспечивать синтаксическая единица, которая может инкапсулировать определение типа и подпрограмму определения операций абстракции
Параллельно Pascal, Smalltalk, C++ и Java напрямую поддерживают абстрактные типы данных
Немного проблемы проектирования, выходящие за рамки инкапсуляции, заключаются в том, какие виды типов могут быть абстрактные должны быть ограничены, могут ли абстрактные типы данных быть параметризованы, и какие средства управления доступом предоставляются, и как такие средства управления указанный
ЯЗЫК ПРИМЕРЫ
Simula 67
-
Данные
абстракция, хотя и неполная по определению, появилась в конструкции класса
Симула 67.
- Simula классы являются динамическими в куче, что означает, что они создаются динамически в куче по запросу программы пользователя
- Simula Вклад 67 в абстракцию данных — инкапсуляция класса построить.
- Переменные объявленные в классе Simula 67, не скрыты от клиентов, создающих объекты этого класса, нарушающие требование сокрытия информации определения абстрактного типа данных.
- Simula Классы 67s гораздо менее надежны, чем настоящий абстрактный тип данных, из-за нарушение.
- Несмотря на то что Конструкция класса Simula 67 обеспечивает инкапсуляцию, но не обеспечивает сокрытие информации.
Ада
- Ада предоставляет средства инкапсуляции, которые можно использовать для имитации абстрактных данных. типов, включая возможность скрывать их представления.
- конструкции инкапсуляции в Аде называются пакетами .
- Каждый пакет состоит из двух частей.
- Первый, это 9Пакет спецификаций 0603, который обеспечивает интерфейс инкапсуляции
-
Второй,
это пакет тела , , который обеспечивает реализацию сущностей,
назван в спецификации.
- пользователь может сделать объект видимым для клиентов или предоставить только информация об интерфейсе.
Модуль-2
- модули Модулы-2 аналогичны пакетам Ады, поэтому они обеспечивают аналогичный уровень поддержки абстрактных типов данных
- Основное различие между ними состоит в том, что в Модуле-2 все типы, представления, скрытые в модулях, должны быть указателями.
С++
- В отличие от Ады и Модулы-2, которые обеспечивают инкапсуляцию, которая может используемый для имитации абстрактных типов данных, C++ предоставляет класс, который более непосредственная поддержка абстрактных типов данных
- данные, определенные в классе, называются членами данных ; функции, определенные в классе называются функции-члены .
- Классы может содержать как скрытые, так и видимые сущности.
Ява
- Java поддержка абстрактных типов данных аналогична C++
- Там однако есть несколько отличий, например, все пользовательские типы данных в Java классы и все объекты выделяются из кучи и доступны через ссылочные переменные и поддержка абстрактных типов данных в Java могут быть только определено в классах
-
Ява
также включает пакеты в качестве одной из своих конструкций инкапсуляции.
ПАРАМЕТРИЗИРОВАННЫЙ РЕЗЮМЕ ТИПЫ ДАННЫХ
А параметризованный абстрактный тип данных означает, что тип данных является общим
Оба Ада и C++ допускают общие или параметризованные абстрактные типы данных
Эти общие типы считаются шаблонами
Отображение абстракции и разделения на классы и объекты
Отображение абстракции и разделения на классы и объектыЦентры разработки программного обеспечения по представлению абстракций в форме, позволяет управлять ими внутри программной системы. Абстракция описывался как совокупность атрибутов и поведение. Как показано на рисунке ниже, атрибуты абстракции сопоставляются с набором данных (переменные, массив, списки, сложные структуры данных и т. д.), а поведение абстракции сопоставляется с набором методов (также известных как операции, функции, действия). Рендеринг абстракций в программном обеспечении всегда был неявная цель программирования, хотя она могла быть омрачена более механическими соображениями.
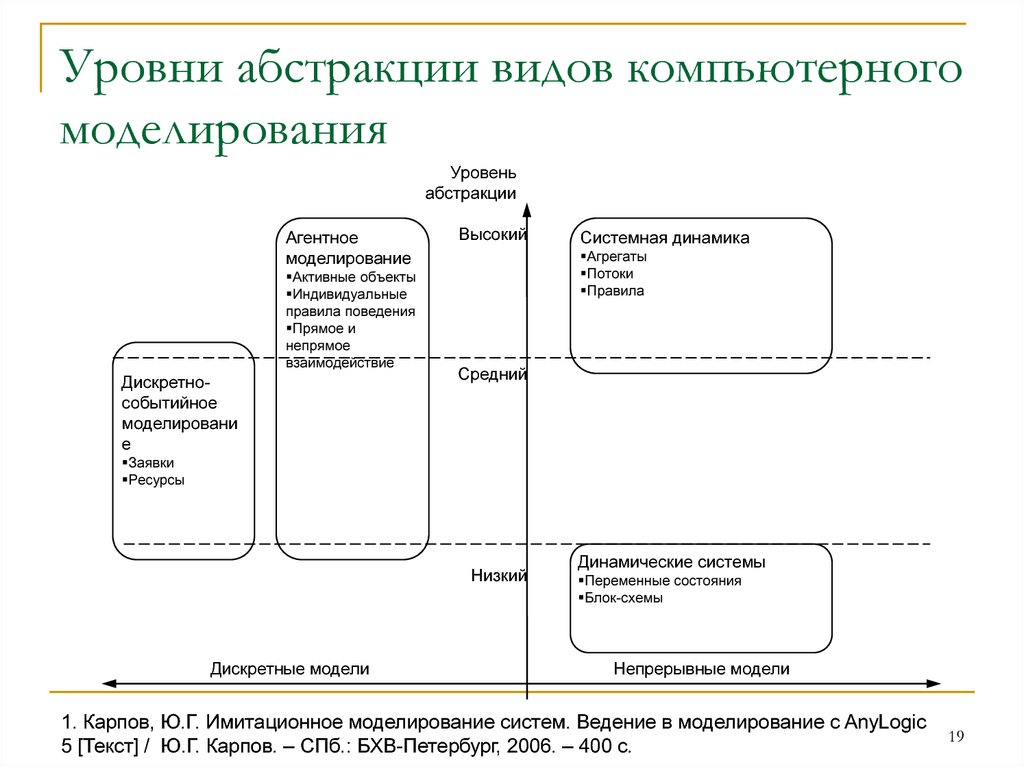
| Сопоставление абстракций с программным обеспечением |
|---|
Что объектно-ориентированное программирование привносит в задачу захвата абстракции в программном обеспечении представляют собой более сложные структуры, а именно классы и объекты , для представления абстракции. Эти новые программные структуры позволяют использовать абстракции. представлено более легко, более непосредственно и более явно. Обучение как использовать существующие классы для создания объектов и управления ими. первый шаг в изучении объектно-ориентированного программирования. Как пользователь, вы можете извлечь выгоду из тяжелой работы, уже проделанной дизайнер и реализатор существующих классов. Эта способность повторно использовать существующие классы — одно из основных преимуществ повторного использования ПО, т. вообще и объектно-ориентированное программирование в частности.
Класс
Класс определяет конкретную структуру данного абстракция (какие у нее данные, какие у нее методы, как ее методы реализуются). Класс имеет уникальное имя
который передает смысл абстракции, которую он представляет.
термин «класс» используется, чтобы предположить, что он представляет всех членов
данная группа (или класс). Например, класс SalesPerson может
представляют всех лиц в группе «людей, продающих автомобили по
автосалон». Объект представляет собой конкретного члена этого
группа.
Класс имеет уникальное имя
который передает смысл абстракции, которую он представляет.
термин «класс» используется, чтобы предположить, что он представляет всех членов
данная группа (или класс). Например, класс SalesPerson может
представляют всех лиц в группе «людей, продающих автомобили по
автосалон». Объект представляет собой конкретного члена этого
группа.Отделение интерфейса от реализации используется для разделения класс на две части, обычно называемые частный часть и публичная часть . Данные и методы отображаются на эти две части класса, как показано ниже. Это разделение закрытые данные и код из видимых имен методов мотивированы многолетним опытом разработки программного обеспечения, показывающим, что это важно защитить данные от непредвиденных, нежелательных и ошибочный доступ из других частей программного обеспечения, которое манипулирует объект. Разделение также служит для сокрытия алгоритма, используемого для выполнить метод.
| Общая структура класса |
|---|
Отношение класса к абстракции и разделению отражено в следующем определении:
- Класс
- Именованное программное представление для абстракции, которая разделяет
реализация представления из интерфейса
представление.

это Интересно отметить, что существуют объектно-ориентированные языки, которые не иметь классов, но использовать другие методы для достижения аналогичного эффект. Языки, такие как C++, Java и другие, которые имеют класс концепции называются «языками, основанными на классах».
Объект
В то время как класс определяет структуру всего набора подобных вещи (например, любой, кто является продавцом), объект представляет собой конкретный экземпляр этого класса (например, продавец, чье имя «Джон Смит», у которого ставка комиссии 15% и т. д.). Определение класса позволяет определить общую структуру один раз. и повторно используется при создании новых объектов, которым нужна определенная структура по классу. Свойства объекта в точности описываются класс, из которого он был создан. Ключевые аспекты структуры объекта, как показано ниже, отражают
структура класса, из которого он был создан. Как и в случае с классом,
двумя основными частями объекта являются его:
Как и в случае с классом,
двумя основными частями объекта являются его:
- реализация: данные и реализация методов которые скрыт внутри объекта, и
- интерфейс: сигнатура всех методов, видимых за пределами объект.
- Инкапсуляция
- в объектно-ориентированном программировании ограничение доступа к данным внутри объекта только те методы, которые определены класс объекта.
| Общая структура объекта |
|---|
Термин экземпляр используется для описания акта создания
объект из класса, и объект называется экземпляр г. класс. Для данного класса могут быть созданы многочисленные экземпляры, каждый из которых
получение отдельного объекта. Это приводит к определению объекта как:
класс. Для данного класса могут быть созданы многочисленные экземпляры, каждый из которых
получение отдельного объекта. Это приводит к определению объекта как:
- Объект
- отдельный экземпляр данного класса, который инкапсулирует детали его реализации и структурно идентичен всем другим экземплярам этого класса.

| Несколько экземпляров класса |
|---|
Связь между классом и объектами, которые могут быть созданы использование класса часто сравнивают с фабрикой и вещами. производства этого завода. Автомобильный завод выпускает автомобили таким же образом, как класс Automobile можно использовать для создания Автомобильные объекты. Кроме того, класс «Автомобиль» может производить только Автомобильные объекты так же, как автомобильный завод, может производить только автомобили, а не пылесосы или ракеты.
Антропоморфизм
Классы и объекты часто обсуждаются разработчиками в реалистичной, личные, антропоморфные термины. Разработчик может сказать, что «класс не должен нести за это ответственность." или "Я ожидаю, что объект ответит на запросы о его текущем состоянии». Разработчик может даже предположить идентичность объекта, чтобы лучше понять роль объекта в конструкции системы. В этом режиме разработчик может спросить: «Что такое ожидать от меня?», «Как я смогу это сделать?» или «Почему вы хотите узнать это обо мне?». Подобные вопросы часто вызывают
разработчика к лучшему интуитивному пониманию объектов и их
отношению к другим объектам.
Подобные вопросы часто вызывают
разработчика к лучшему интуитивному пониманию объектов и их
отношению к другим объектам.Простой и популярный прием дизайна интуитивно связан с антропоморфный взгляд на предметы. Эта техника фокусируется на определение для каждого объекта (или класса объектов) его обязанности и его сотрудников . Объект (или класс) обязанности — это те свойства или обязанности, которые объект (или класс) обязан поддерживать или выполнять. объект соавторы (или класса) — это другие объекты (или классы) с с которыми данный объект (или класс) должен взаимодействовать. Условия «обязанности» и «сотрудники» отражают антропоморфное просмотр предметов.
Олицетворение предметов отражает соответствие разработчиков
видеть между сущностью реального мира и ее абстракцией, с одной
стороны, а также классы и объекты, которые являются их программным обеспечением.
аналоги, с другой. Эта точка зрения также отражает автономию и
инкапсуляция, назначаемая разработчиками объектам и классам.
|
3. Объекты и абстракция. Документация по объектно-ориентированному программированию
В этой главе мы впервые рассмотрим представление
абстрактные математические объекты и операции как объекты данных в
компьютерная программа. Мы узнаем о том, что означает, что объекты имеют
тип и как создавать новые типы с помощью класс ключевое слово.
3.1. Абстракция в действии
Рассмотрим эту строку кода Python:
печать (а + б)
Что он делает? Что ж, если предположить, что a и b правильно определены, то
печатает их сумму. Это, однако, вызывает вопросы: что является «соответствующим образом
определено», а что такое «сумма»? Например:
Это, однако, вызывает вопросы: что является «соответствующим образом
определено», а что такое «сумма»? Например:
В [1]: а = 1 В [2]: b = 2 В [3]: напечатать (a + b) 3
Вас вряд ли удивит, что Python может складывать целые числа. С другой стороны, оказывается, мы можем добавить и строки:
В [1]: a = 'fr' В [2]: b = 'ог' В [3]: напечатать (a + b) 'лягушка'
Таким образом, значение + зависит от того, что добавляется. Что произойдет, если
мы добавляем целое число к строке?
В [1]: а = 1 В [2]: b = 'ог' В [3]: напечатать (a + b) -------------------------------------------------- ------------------------- TypeError Traceback (последний последний вызов)в <модуле> ----> 1 печать (а + б) TypeError: неподдерживаемые типы операндов для +: 'int' и 'str'
В этой ошибке Python жалуется, что + не имеет смысла, если
добавляемые элементы (операнды) являются целым числом и
нить. Это делает наше понимание «должным образом определенным» более
конкретные: очевидно, что некоторые пары объектов могут быть добавлены, а другие
не мочь. Однако нам следует быть осторожными в выводах, которые мы делаем. Мы
может возникнуть соблазн поверить, что мы можем добавить два значения, если они
того же типа. Однако, если мы попробуем это с парой наборов, то мы
тоже в беде:
Это делает наше понимание «должным образом определенным» более
конкретные: очевидно, что некоторые пары объектов могут быть добавлены, а другие
не мочь. Однако нам следует быть осторожными в выводах, которые мы делаем. Мы
может возникнуть соблазн поверить, что мы можем добавить два значения, если они
того же типа. Однако, если мы попробуем это с парой наборов, то мы
тоже в беде:
В [1]: а = {1, 2}
В [2]: b = {2, 3}
В [3]: напечатать (a + b)
-------------------------------------------------- -------------------------
TypeError Traceback (последний последний вызов)
в <модуле>
----> 1 печать (а + б)
TypeError: неподдерживаемые типы операндов для +: 'set' и 'set'
И наоборот, мы могли бы предположить, что два значения могут быть добавлены, только если они одного и того же значения. тип. Однако совершенно законно добавлять целое и плавающее количество баллов:
В [1]: а = 1 В [2]: b = 2,5 В [3]: напечатать (a + b) 3,5
В Python оператор + кодирует абстракцию для сложения. Это означает
что
Это означает
что + означает операцию сложения, что бы это ни значило для
конкретная пара операндов. Для целей абстракции,
все, что относится к конкретным операндам,
игнорируется. Сюда входят, например,
механизм, с помощью которого вычисляется добавка, и значение
результат. Это позволяет программисту думать об относительно простых
математическая операция сложения, а не потенциально
сложным или запутанным способом, которым это может быть реализовано для конкретных данных.
Определение 3.1
Абстракция представляет собой математический объект с ограниченным набором определенные свойства. Для целей абстракции любой другой свойства, которыми может обладать объект, игнорируются.
Абстракция — это чисто математическое понятие, но оно
сопоставляется с одной или несколькими конкретными реализациями в коде. Иногда
абстрактное математическое понятие и его конкретная реализация совпадают настолько
прекрасно, что их трудно различить. В тех
обстоятельств, мы обычно объединяем терминологию для абстракции
и объект кода. «Тип» — один из таких примеров, и мы обратимся к нему.
в настоящее время.
«Тип» — один из таких примеров, и мы обратимся к нему.
в настоящее время.
3.2. Типы
В предыдущем разделе мы заметили, что сложение может быть, а может и не быть. определяется в зависимости от типов его операндов. При этом мы обошли вопрос о том, что значит для объекта иметь тип.
Определение 3.2
Тип или класс — это абстракция, определяемая набором возможных значений, и набор операторов, действительных для объектов этого типа.
Каждый объект в Python имеет тип. Это верно для примитивных числовых
типы, такие как in , float и complex ; для таких последовательностей, как
строка ( str ), кортеж и список ; а также для более сложных типов
например, , набор и словарь ( dict ). Действительно,
Концепция типа в Python идет гораздо дальше, поскольку мы обнаружим, если вызовем типа на разных объектах:
В [1]: тип(1) Выход[1]: интервал В [2]: введите (абс) Выход[2]: встроенная_функция_или_метод
Итак, 1 является объектом типа int , что означает, что он поставляется со всеми
Операции Python для целочисленной арифметики.
abs() , с другой стороны,
является встроенной функцией, поэтому ее определяющая операция заключается в том, что ее можно
вызывается по одному или нескольким подходящим аргументам (например, abs(1) ). Если
у каждого объекта есть тип, а как насчет самих типов? Какой тип
из целое ?
В [1]: тип (целое) Выход[1]: тип
Мы видим, что int является типом целочисленных объектов и сам является
объект с типом тип . Это скорее вызывает вопрос о том, что
тип типа ?
В [1]: тип(тип) Выход[1]: тип
Это действительно имеет смысл, потому что типа — это просто
тип типов.
Позже мы вернемся к типам более подробно. На этом этапе Главная идея заключается в том, что практически все, с чем вы столкнетесь в Python — это объект, и у каждого объекта есть тип.
Примечание
В Python термин
«класс» по сути является синонимом «типа», поэтому «что такое класс
из foo »то же самое, что сказать «какой тип foo ». Однако
эти два термина не являются синонимами при использовании в коде.
Однако
эти два термина не являются синонимами при использовании в коде. тип может быть
используется для определения типа объекта, а класс используется для определения новых типов.
3.3. Определение новых типов
Видео: первый классИмперские студенты также могут посмотреть это видео на Panopto
Python имеет богатый набор встроенных типов. Они образуют мощные строительные блоки для языке, но очень скоро можно найти математические абстракции, которые не имеют реализации среди встроенных типов Python устный переводчик. Например, встроенные типы не включают матрицу или тип многомерного массива. Возможность создавать новые типы данных которые обеспечивают конкретные реализации дальнейших математических абстракций является центральным элементом эффективного использования абстракций в программирование. 9n \quad \textrm{для некоторых } d\in \mathbb{N}, c_n \in \mathbb{R}\]
Множество всех многочленов является четко определенным (хотя и бесконечным) множеством
различные значения, с рядом четко определенных свойств. За
Например, мы можем складывать и умножать многочлены, в результате чего получается новый
многочлен. Мы также можем вычислить полином для определенного значения
из \(x\), что привело бы к действительному значению.
За
Например, мы можем складывать и умножать многочлены, в результате чего получается новый
многочлен. Мы также можем вычислить полином для определенного значения
из \(x\), что привело бы к действительному значению.
Это математическая абстракция многочлена. Как бы мы
представить эту абстракцию в коде Python? Многочлен
характеризуется своим набором коэффициентов, так что в принципе можно было бы
представить многочлен в виде кортеж коэффициента
ценности. Однако добавление кортежей является конкатенацией, и
умножение двух кортежей даже не определено, так что это было бы
очень плохое представление математики: многочлен представлен
как кортеж коэффициентов не будет вести себя так, как математик
ожидать. Вместо этого нам нужно создать новый тип, чей
операции соответствуют математическим свойствам многочлена.
3.3.1. Классы и конструкторы
Ключевое слово Python для объявления нового типа:
9я\).
Это упростит логику программы, но будьте осторожны, потому что математики
обычно записывают коэффициенты от наибольшей степени \(x\) к наименьшей, и это
противоположно этому. Выполнение этого кода в интерпретаторе Python позволит нам создать
простой многочлен и проверьте его коэффициенты:
Выполнение этого кода в интерпретаторе Python позволит нам создать
простой многочлен и проверьте его коэффициенты:
В [7]: f = Polynomial((0, 1, 2)) В [8]: f.коэффициенты Выход[8]: (0, 1, 2)
Три строки Python, определяющие класс Polynomial , содержат
несколько важных концепций и деталей Python, которые важно знать
понять.
Оператор определения класса открывает новый блок, поэтому
как и определение функции, оно начинается с
ключевое слово, за которым следует имя класса, который мы определяем, и
заканчивается двоеточием. Пользовательские классы в Python (т. е. классы, не
встроенные в язык) обычно имеют имена CapWords. Это означает
что все слова в имени пишутся с заглавной буквы и идут вместе без пробелов. За
например, если мы решили сделать отдельный класс для комплекснозначных
многочленов, мы могли бы назвать его ComplexPolynomial .
Внутри определения класса, т.е. с отступом внутри блока, находится
функция называется __init__() . Функции, определенные внутри класса
определения называются методами. Метод
Функции, определенные внутри класса
определения называются методами. Метод __init__() имеет
довольно характерная форма имени, начинающаяся и заканчивающаяся двумя
подчеркивает. Имена этого формата используются в языке Python для
объекты, которые имеют особое значение в языке Python. __init__() метод класса имеет особое значение в Python, поскольку
конструктор класса. Когда мы пишем:
В [7]: f = Polynomial((0, 1, 2))
Это называется созданием экземпляра объекта типа Многочлен . Происходят следующие шаги:
Python создает объект типа
Polynomial.__init__()специальный метод полиномаPolynomialпередается как первый параметр (self) и кортеж(0, 1, 2)пройдено в качестве второго параметра (коэф.).Имя
fв окружающей области связано сМногочлен.
Примечание
Обратите внимание, что Polynomial.__init__() ничего не возвращает. Роль
метода __init__() заключается в настройке объекта, self ; Это
не вернуть значение. __init__() никогда не возвращает значение.
3.3.2. Атрибуты
Теперь посмотрим, что произошло внутри метода __init__() . Мы
иметь только одну строку:
собственные коэффициенты = коэффициенты
Помните, что self — это объект, который мы настраиваем, а coefs — это
другой параметр для __init__() . Эта строка кода создает новый
name внутри этого объекта Polynomial , называемого коэффициенты и связывает это новое имя с объектом, переданным как
аргумент Полиномиальный конструктор. Такие имена, как
это называется атрибутами. Мы создаем атрибут
просто назначив ему, и мы можем затем прочитать атрибут, используя
тот же синтаксис, который мы сделали здесь:
В [8]: f.коэффициенты Выход[8]: (0, 1, 2)
Атрибутам может быть присвоено любое имя, которое разрешено для имени Python в целом — то есть последовательности букв, цифр и знаков подчеркивания, начинающиеся с буква или подчеркивание. Особое значение имеют имена, начинающиеся с подчеркивание, поэтому их следует избегать в ваших собственных именах, если вы не собираетесь создать частный атрибут.
3.3.3. Методы
Видео: определение методовImperial Студенты также могут посмотреть это видео на Panopto
Мы уже встречались со специальным методом __init__() ,
который определяет конструктор класса. Гораздо более характерен случай
обычный метод, без специального имени подчеркивания. Например,
предположим, что мы хотим получить доступ к степени многочлена, тогда
мы могли бы добавить в наш класс метод Degree() :
:
def __init__(я, коэффициенты):
селф. коэффициенты = коэфф.
Степень защиты (я):
вернуть len (собственные.коэффициенты) - 1
коэффициенты = коэфф.
Степень защиты (я):
вернуть len (собственные.коэффициенты) - 1
Обратите внимание, что новый метод имеет отступ внутри класса блок на том же уровне, что и метод __init__() . Соблюдайте также
что он тоже принимает self в качестве своего первого параметра. Ключевое отличие от
метод __init__() заключается в том, что Degree() теперь возвращает
value, как и большинство функций. Теперь мы можем использовать наш новый метод для восстановления
степень нашего многочлена.
В [1]: f = многочлен ((0, 1, 2)) В [2]: f.степень() Выход[2]: 2
Чтобы уточнить роль параметра self , он помогает понять
что f.степень() - это просто короткий способ записи Многочлен.степень(f) . Подобно атрибутам, методы могут иметь любые допустимые значения Python.
имя. Атрибуты и методы объекта являются частью одного и того же
пространство имен, поэтому у вас не может быть атрибута и метода с одинаковыми
имя.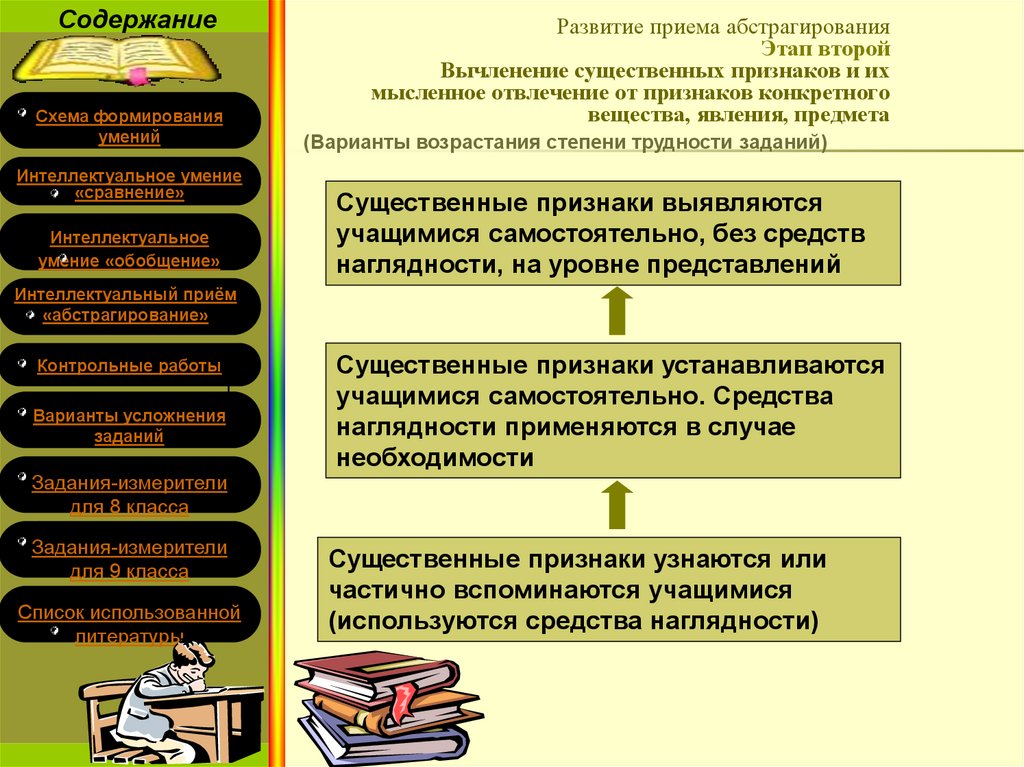 Если вы попытаетесь, то имя будет перезаписано тем, что было определено
позже, и атрибут или метод, определенный первым, больше не будет доступен
под этим именем. Это вряд ли то, что вы хотели.
Если вы попытаетесь, то имя будет перезаписано тем, что было определено
позже, и атрибут или метод, определенный первым, больше не будет доступен
под этим именем. Это вряд ли то, что вы хотели.
Примечание
Сам объект всегда передается в качестве первого аргумента метода.
Технически, первый параметр можно назвать любым допустимым Python.
имя, но существует очень строгое соглашение, что первый параметр для
любой метод экземпляра называется self . Никогда, никогда не назови это
параметр ничего, кроме self , или вы запутаете каждый Python
программист, который читает ваш код!
3.3.4. Строковые представления объектов
Видео: уроки полиграфииImperial Студенты также могут посмотреть это видео на Panopto
Помните, что основной причиной определения новых классов является предоставление пользователям возможности
рассуждать о полученных объектах на более высоком математическом уровне. Ан
Важным подспорьем для пользователя в этом является возможность посмотреть на
объект. Что произойдет, если мы напечатаем полином
Ан
Важным подспорьем для пользователя в этом является возможность посмотреть на
объект. Что произойдет, если мы напечатаем полином ?
В [1]: f = многочлен ((0, 1, 2)) В [2]: print(f) <Полиномиальный объект по адресу 0x104960dd0>
Это менее чем полезно. По умолчанию Python просто печатает класс объект и адрес памяти, по которому находится этот конкретный объект хранится. Впрочем, это не так уж и удивительно, если подумать о ситуацию чуть глубже. Откуда Python должен был знать, что строковое представление имеет смысл для этого объекта? Мы будем должен сказать это.
Мы делаем это с помощью другого специального метода. Специальный
имя метода для удобочитаемого строкового представления объекта __str__() . Он не принимает никаких аргументов, кроме самого объекта.
В листинге 3.1 представлена одна из возможных реализаций этого метода.
Листинг 3.1. Реализация строкового представления Многочлен . 3 + 2х + 1
3 + 2х + 1
На самом деле Python предоставляет не один, а два специальных
методы, преобразующие объект в
нить. __str__() вызывается print() , а также ул . Его роль заключается в предоставлении строкового представления, которое
лучше всего понимают люди. В математическом коде это обычно
быть математическим обозначением объекта. Напротив, Метод __repr__() вызывается repr() и также предоставляет
строковое представление по умолчанию, распечатываемое командой Python
линия. По соглашению __repr__() должна возвращать строку, которую
пользователь может ввести, чтобы воссоздать объект. Например:
определение __repr__(сам):
возвращаемый тип (self).__name__ + "(" + repr (self.coefficients) + ")"
type(self).__name__ просто вычисляет имя класса, в данном случае Многочлен . Это лучше, чем жестко кодировать имя класса, потому что, как мы
см. в главе 7, эта реализация __repr__() вполне может оказаться унаследованным классом с
другое имя. Обратите внимание, что для обеспечения согласованности
представления мы называем
Обратите внимание, что для обеспечения согласованности
представления мы называем repr() на коэффициенты в этом случае, тогда как
в методе __str__() мы вызвали str .
Теперь мы можем наблюдать разницу в результате:
В [2]: f = многочлен ((1, 2, 0, 4, 5)) В [3]: ф Out[3]: полиномиальный ((1, 2, 0, 4, 5))
3.3.5. Равенство объектов
Видео: равенство объектов и разработка через тестированиеСтуденты Imperial также могут посмотреть это видео на Panopto
Когда два объекта равны? Для встроенных типов Python имеет правила равенства, которые в целом соответствуют математическим тождествам, которые вы могли бы ожидать. Например, два числа разных типов равны, если их числовое значение равно:
В [1]: 2 == 2,0 Выход[1]: Истина В [2]: 2,0 == 2+0j Выход[2]: Истина
Аналогично, внутренние типы последовательностей равны, когда их содержимое равно:
В [3]: (0, 1, "f") == (0., 1+0j, 'f') Выход[3]: Истина В [4]: (0, 1, "f") == (0., 1+0j, 'g') Выход[4]: Ложь В [5]: (0, 1, "f") == (0., 1+0j) Выход[5]: Ложь
Это математически приятное положение дел, однако, не переходить в новые классы. Можно было бы ожидать, что два одинаково определенных полиномы могут сравниваться равными:
В [6]: from example_code.polynomial import Polynomial В [7]: a = Polynomial((1, 0, 1)) В [8]: b = Polynomial((1, 0, 1)) В [9]: а == б Выход[9]: Ложь
Причина этого очевидна, если подумать: Python не может
знать, когда два экземпляра нового класса следует считать равными. Вместо этого это
возвращается к сравнению уникальной идентичности каждого объекта. Это доступно
используя встроенную функцию id() :
В [10]: id(a) Выход[10]: 4487083344 В [11]: id(b) Выход[11]: 4488256096
Это прекрасно определенный оператор равенства, но не очень
математически полезный. К счастью, Python позволяет нам определить более полезный
оператор равенства с использованием специального метода __eq__() .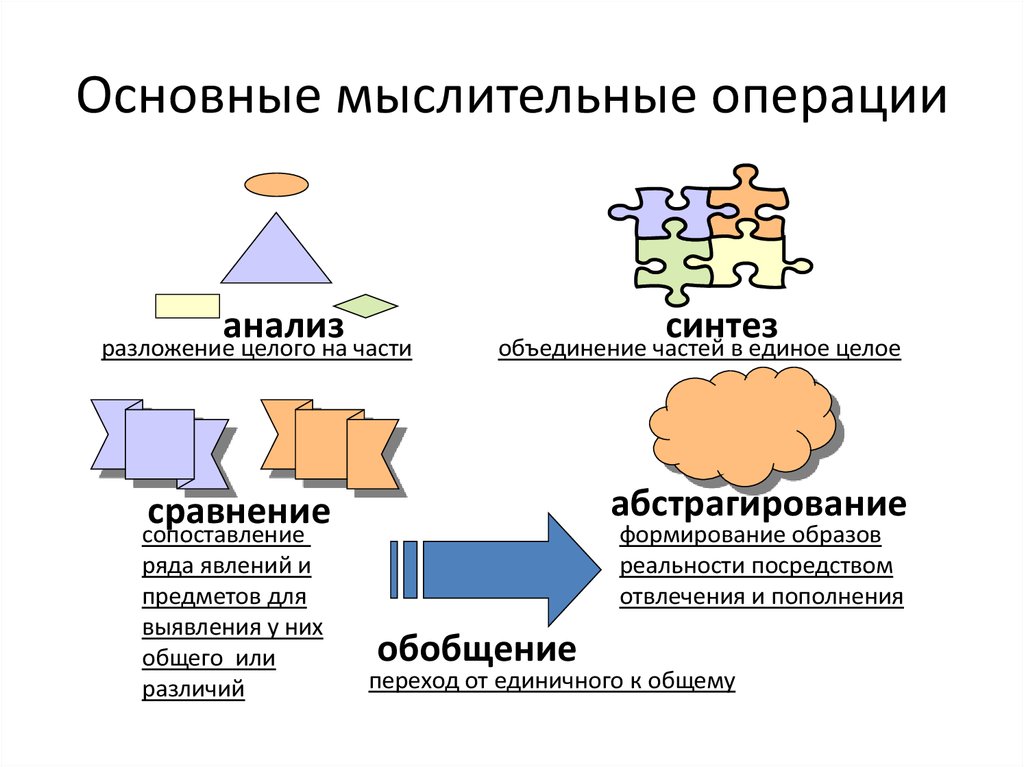 Этот
берет текущий объект и объект, с которым он сравнивается, и возвращает
Этот
берет текущий объект и объект, с которым он сравнивается, и возвращает True или False в зависимости от того, должны ли объекты
считаются равными. Когда мы пишем a == b на Python, на самом деле происходит следующее: а.__экв__(б) .
Базовая реализация __eq__() , которая проверяет, что другой
объект представляет собой полином с тем же
коэффициенты:
def __eq__(я, другой):
return isinstance(other, Polynomial) и \
селф.коэффициенты == другие.коэффициенты
Оснащен этим методом, Полиномиальный равенство теперь ведет себя так, как мы могли бы ожидать.
В [1]: from example_code.polynomial import Polynomial В [2]: a = Polynomial((1, 0, 1)) В [3]: b = Polynomial((1, 0, 1)) В [4]: а == б Выход[4]: Истина
3.3.6. Определение арифметических опций для объектов
Видео: полиномиальное сложение.Имперские студенты также могут посмотреть это видео на Panopto
Очень хорошо иметь возможность сравнивать наши полиномиальные объекты, но
мы действительно не уловили математическую абстракцию, связанную с
если у нас нет хотя бы некоторых математических операций. Мы уже
заметил, что объекты некоторых классов могут быть добавлены. Верно ли это для Многочлен с?
В [2]: a = Polynomial((1, 0)) В [3]: b = Polynomial((1,)) В [4]: а + б -------------------------------------------------- ------------------------- TypeError Traceback (последний последний вызов)в <модуле> ----> 1 а + б TypeError: неподдерживаемые типы операндов для +: «Полиномиальный» и «Полиномиальный»
Конечно, опять же это не так уж удивительно, поскольку мы не
определил, что должно означать сложение полиномов. Специальный
метод, который определяет добавление, __add__() . Это занимает
самого объекта и другого объекта и возвращает их сумму.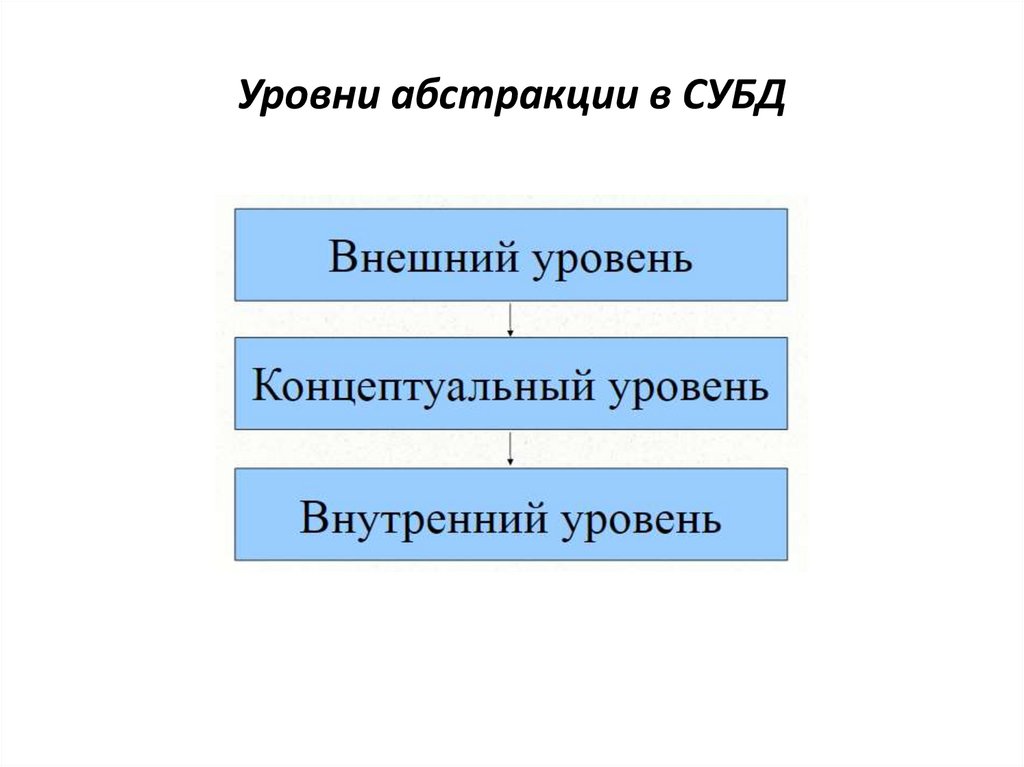 То есть,
когда вы пишете
То есть,
когда вы пишете a + b в Python, то на самом деле происходит следующее: а.__добавить__(б) .
Прежде чем мы определим наш метод сложения, мы сначала должны рассмотреть, что другие объекты, возможно, имеет смысл добавить к многочлену. Очевидно, мы должна иметь возможность сложить два полинома, но также имеет смысл добавить число к многочлену. В любом случае результатом будет новый многочлен с коэффициентами, равными сумме коэффициентов слагаемые.
Нам также нужно что-то сделать в случае, когда пользователь пытается добавить в
полиномиальное значение, для которого операция не имеет смысла. Например, пользователь
может случайно попытаться добавить строку к многочлену. В этом случае
Спецификация языка Python требует, чтобы мы возвращали специальное значение Не реализовано . Различие между типами операндов требует
еще две возможности Python, с которыми мы еще не встречались. Одним из них является встроенный
функция isinstance() , который проверяет, является ли объект экземпляром
учебный класс. Другой — это класс
Другой — это класс Number , который мы импортируем из
встроенный модуль номеров . Все числа Python являются экземплярами Номер , так что это обеспечивает механизм для проверки того,
другой операнд является числом. Мы рассмотрим isinstance() и Число более подробно, когда мы рассмотрим наследование и абстрактные базовые классы.
Собрав все это вместе, листинг 3.2 определяет полиномиальное сложение.
Листинг 3.2. Реализация сложения для полинома .
1def __add__(я, другой): 2 если isinstance (другое, число): 3 вернуть полиномиальный((self.coefficients[0] + другое,) 4 + собственные.коэффициенты[1:]) 5 6 elif isinstance (другое, полиномиальное): 7 # Определите, сколько мест коэффициентов имеют два полинома в 8 # общ. 9 общее = мин (self.степень(), другое.степень()) + 1 10 # Суммировать позиции общего коэффициента. 11 коэффициентов = кортеж (a + b для a, b в zip (self.coefficients [: common], 12 других.коэффициентов[:общие])) 13 14 # Добавляем коэффициенты старшей степени из старшей степени 15 # слагаемое. 16 коэффициентов += собственные.коэффициенты[общие:] + другие.коэффициенты[общие:] 17 18 обратных полиномов (коэффициенты) 193 + 2x + 2 В [8]: print(1 + a) -------------------------------------------------- ------------------------- TypeError Traceback (последний последний вызов)
в <модуле> ----> 1 печать (1 + а) TypeError: неподдерживаемые типы операндов для +: 'int' и 'Polynomial'
Итак, все идет как положено, пока мы не попытаемся добавить Полином от до целого числа. Что случилось? Помните, что 1 + заставляет Python вызывать внутр.__доб.__(1, а) . Что это делает?:
В [9]: int.__add__(1, а) Out[9]: Не реализовано
Естественно, встроенный в Python тип int ничего не знает о нашем
новый класс Polynomial , поэтому, когда мы просим его выполнить сложение,
он возвращает NotImplemented . 3 + 2х + 2
3 + 2х + 2
Конечно, сложение — не единственный арифметический оператор, который можно было бы пожелать. перегрузить. Полнофункциональный полиномиальный класс будет в самом минимум, нужно вычитание, умножение (на скаляр или другой многочлен) и возведение в степень в целой степени. Сочетание они, и особенно возведение в степень, позволят пользователю определить новые полиномы особенно естественным образом, используя Python внутренние операторы:
В [1]: x = многочлен ((0, 1)) В [2]: печать (х) Икс В [3]: р = х**3 + 2*х + 2 В [4]: с. Полиномиальный ((2, 2, 0, 1)) 92 + 2х + 1\], то для любого действительного \(x\) \(f(x)\) определено и является действительным количество. Мы уже знаем из примера
abs()выше, что Функции Python — это объекты. Однако наша задача состоит в обратном это: у нас естьполиномиальныхобъекта, которыми мы хотели бы быть возможность вызывать подобные функции. Решение нашей задачи состоит в том, что вызов функции — это операция над объектом, аналогичная сложению, и Python предоставляет другое специальное имя метода для это.
f(x)сопоставляется сf.__call__(x), поэтому любой объект Python сМетод __call__()ведет себя как функция и любой класс определение метода__call__()фактически определяет новый тип функция.3.4. Инкапсуляция
Свойство объектов объединять данные и методы в более или менее непрозрачный объект, с которым другой код может взаимодействовать без занимающийся внутренними деталями предмета, называется инкапсуляция. Инкапсуляция является одним из основных понятий в объектно-ориентированного программирования. В частности, инкапсуляция является ключом к создание отдельных объектов, представляющих математические абстракции, конкретная реализация которых в коде может потребовать многих фрагменты данных и большое количество сложных функций.
3.5. Глоссарий
- абстракция
Математическая концепция с ограниченным набором определенных характеристики. Для целей абстракции любой другой свойства, которыми может обладать объект, игнорируются.

- атрибут
Значение, инкапсулированное в другой объект, например учебный класс. Доступ к атрибутам осуществляется с использованием точечного синтаксиса, поэтому, если
bявляется атрибутомa, тогда доступ к его значению осуществляется с помощью синтаксиса.б.. Методы являются частным случаем атрибутов.- класс
- тип
Абстракция, определяемая набором возможных значений и набором операторов, допустимых для объектов этого типа.
КлассиТиппо существу являются синонимами, хотя эти два слова играют разные роли в коде Python.- конкатенация
Объединение двух последовательностей путем создания новой последовательности, содержащей все элементы в первой последовательности, за которыми следуют все элементы в вторая последовательность. Например
(1, 2) + (3, 4)равно(1, 2, 3, 4).- конструктор
Метод
__init__()класса.Конструктор передается новый объект в качестве первого аргумента (
self) и ответственный за настройку объекта. Конструктор изменяетselfна месте: конструкторы никогда не возвращают значение.- атрибут данных
Атрибут, который не является методом. Как имя предполагает, что они используются для хранения данных в объекте.
- инкапсуляция
Объединение атрибутов и методов в объект, который можно рассматривать как единое целое.
- Инфиксный оператор
Математический оператор, символ которого записывается между его операндами. Примеры включают сложение, вычитание, деление и умножение.
- экземпляр
Объект определенного класса.
aявляется экземпляромMyClassозначает, чтоимеет классMyClass. Мы будем вернуться к этой концепции, когда мы узнаем о наследовании.- создать экземпляр
Чтобы создать экземпляр класса с помощью вызов его конструктора.

- метод
- метод экземпляра
Функция, определенная в классе. Если
- это. экземплярMyClassиMyClassимеет методfoo(), затемa.foo()эквивалентноMyClass.foo(a). Первый параметр метода экземпляра всегда называетсяself.- операндов
Входные значения для оператора. Например, операнды для
+являются добавляются числа (слагаемые), а операнды возведения в степень являются основанием и показателем.- псевдокод
Описание алгоритма, представленное в компьютерной форме программе, но без соблюдения правил конкретной язык программирования и использование математических обозначений или обычный текст, чтобы выразить алгоритм в удобочитаемой форме.
- специальный метод
- магический метод
Метод, который имеет особое значение в Python язык. Имена специальных методов используются для определения операций над класс, такой как арифметические операторы, индексирование или конструктор класса.
Специальные методы имеют имена, начинающиеся и заканчивающиеся с двойным подчеркиванием (
__). Техническое описание см. в документации Python. Специальные методы иногда неофициально называют «магическими методами».3.6. Упражнения
Использование информации на сайте книги получить базовый код для этих упражнений. Скелетный код содержит Пакет
polynomialс версией классаPolynomial.Упражнение 3.3
Реализуйте следующие операции над классом
Polynomial.
Вычитание (
__sub__()и__rsub__()).Умножение на другой многочлен и на скаляр (
__mul__()и__rmul__()).Возведение в степень положительного целого числа (
__pow__()). Это может быть полезно знать, что все целые числа являются экземпляраминомера. Интеграл.Полиномиальное вычисление скалярного значения (
__call__()).
Примечание
Не забудьте зафиксировать и отправить изменения, а также убедитесь, что тесты проходят на GitHub!
Упражнение 3.4
Определите метод
dx()для классаPolynomial, который возвращает новыйМногочлен, который является производным от этогоМногочлен. Также определите производную функциивpolynomials.py, который принимает полиноми возвращает его производная. Вместо того, чтобы дублировать код, вы должны реализовать функцию путем вызова метода.Упражнение 3.5
Внутри репозитория упражнений создайте новый
формапакет, содержащий модульCircle.
Создать класс
Circleчей конструктор принимает два пользовательских параметра:centerиradius.центрдолжен быть последовательностью длины 2, содержащей двумерный координаты центра, арадиусарадиуса окружности.
Добавить оператор импорта в
shape/__init__.pyтак что следующий код работает:из импорта формы CircleРеализовать специальный метод
__contains__()наОбведите класстак, чтобы он возвращалTrue, если точка (представленная последовательностью координат длины 2) лежит внутри круга. За Например, следующий код должен напечататьTrue.из импорта формы Circle с = круг ((1., 0.), 2) печать ((0,5, 0,5) в c)Упражнение 3.6
Сделайте
кругимногочленпакеты устанавливаемые. Как с упражнение из последней главы, Pytest не может его протестировать, поэтому вам нужно нажать на GitHub и проверьте, проходят ли там тесты автоградации.Сноски
- 1
https://объектно-ориентированный-python.github.io/edition1/exercises.html
2.4 Несколько представлений абстрактных данных
Мы ввели абстракцию данных, метод структурирования систем
таким образом, что большая часть программы может быть определена независимо от
выбор, связанный с реализацией объектов данных, которые программа
манипулирует. Например, мы видели в
Раздел 2.1.1
как разделить задачу разработки программы, использующей рациональное
номера от задачи реализации рациона номеров в плане
примитивные механизмы компьютерного языка для построения составных данных.
Ключевой идеей было возведение барьера абстракции — в данном случае
селекторы и конструкторы для рациональных чисел — это изолирует
способ использования рациональных чисел из их основного представления
с точки зрения структуры списка. Подобный барьер абстракции изолирует
детали процедур, которые выполняют рациональную арифметику из
процедуры «высокого уровня», использующие рациональные числа.
Например, мы видели в
Раздел 2.1.1
как разделить задачу разработки программы, использующей рациональное
номера от задачи реализации рациона номеров в плане
примитивные механизмы компьютерного языка для построения составных данных.
Ключевой идеей было возведение барьера абстракции — в данном случае
селекторы и конструкторы для рациональных чисел — это изолирует
способ использования рациональных чисел из их основного представления
с точки зрения структуры списка. Подобный барьер абстракции изолирует
детали процедур, которые выполняют рациональную арифметику из
процедуры «высокого уровня», использующие рациональные числа.
Эти барьеры абстракции данных являются мощными инструментами для контроля
сложность. Изолируя базовые представления данных
объекты, мы можем разделить задачу разработки большой программы на
более мелкие задачи, которые можно выполнять отдельно. Но такие данные
абстракция еще недостаточно сильна, потому что она не всегда может сделать
смысла говорить о «основном представлении» для объекта данных.
Во-первых, может быть более одного полезного представления для объект данных, и мы могли бы захотеть разработать системы, которые могут работать с множественные представления. Возьмем простой пример, комплексные числа может быть представлен двумя почти эквивалентными способами: в прямоугольной форме (действительная и мнимая части) и в полярной форме (величина и угол). Иногда более уместна прямоугольная форма, а иногда полярная. форма более подходящая. В самом деле, вполне правдоподобно представить система, в которой комплексные числа представляются обоими способами, а с которыми работают процедуры обработки комплексных чисел либо представление.
Что еще более важно, системы программирования часто разрабатываются многими
люди, работающие в течение длительного периода времени, в соответствии с требованиями
которые меняются со временем. В такой среде просто не
возможность для каждого заранее договориться о выборе данных
представление. Таким образом, в дополнение к барьерам абстракции данных, которые
изолировать представление от использования, нам нужны барьеры абстракции, которые
изолировать различные варианты дизайна друг от друга и разрешить различные
возможности сосуществовать в одной программе. Кроме того, поскольку большое
программы часто создаются путем объединения уже существующих модулей, которые были
разработаны изолированно, нам нужны соглашения, позволяющие программистам
включать модули в более крупные системы аддитивно , то есть без
необходимость перепроектировать или повторно реализовать эти модули.
Кроме того, поскольку большое
программы часто создаются путем объединения уже существующих модулей, которые были
разработаны изолированно, нам нужны соглашения, позволяющие программистам
включать модули в более крупные системы аддитивно , то есть без
необходимость перепроектировать или повторно реализовать эти модули.
В этом разделе мы узнаем, как справляться с данными, которые могут быть
по-разному представлены разными частями программы. Этот
требует построения универсальных процедур процедур, которые могут
работать с данными, которые могут быть представлены более чем одним способом. Наш главный
метод построения общих процедур будет заключаться в том, чтобы работать в терминах
объекты данных, которые имеют теги типа , то есть объекты данных, которые включают
явная информация о том, как они должны быть обработаны. Мы также
обсудить программирование , ориентированное на данные, мощное и удобное
стратегия внедрения для аддитивной сборки систем с универсальными
операции.
Начнем с простого примера комплексного числа. Мы увидим, как тип
теги и ориентированный на данные стиль позволяют нам создавать отдельные прямоугольные
и полярные представления для комплексных чисел, сохраняя при этом
понятие абстрактного объекта данных «комплексное число». Мы будем
выполнить это, определив арифметические процедуры для комплексных чисел
( add-comple , sub-complex , mul-complex и div-complex ) в
термины общих селекторов, которые обращаются к частям комплексного числа
независимо от того, как представлено число. Результирующий
комплексная система счисления, как показано на рисунке ниже, содержит два
различные виды барьеров абстракции. «Горизонтальная» абстракция
барьеры изолируют операции «более высокого уровня» от операций «нижнего уровня».
представления. Кроме того, существует «вертикальный» барьер, который
дает возможность отдельно проектировать и устанавливать альтернативные
представления.
В разделе 2. 5
мы покажем, как использовать теги типов и стиль, ориентированный на данные, для разработки
универсальный арифметический пакет. Это обеспечивает процедуры (
5
мы покажем, как использовать теги типов и стиль, ориентированный на данные, для разработки
универсальный арифметический пакет. Это обеспечивает процедуры ( add , mul ,
и так далее), которые можно использовать для манипулирования всевозможными «числами» и
может быть легко расширен, когда требуется новый тип числа. В
Раздел 2.5.3,
мы покажем, как использовать общую арифметику в системе, которая выполняет
символическая алгебра.
2.4.1 Представления комплексных чисел
Мы разработаем систему, выполняющую арифметические операции над
комплексные числа как простой, но нереалистичный пример программы, которая
использует общие операции. Начнем с обсуждения двух возможных
представления комплексных чисел в виде упорядоченных пар: прямоугольная форма
(действительная и мнимая части) и полярная форма (величина и угол). [В
реальных вычислительных системах прямоугольная форма предпочтительнее полярной
чаще всего из-за ошибок округления при преобразовании между
прямоугольной и полярной формы. Вот почему пример комплексного числа
нереально. Тем не менее, это дает четкую иллюстрацию
проектирование системы с использованием общих операций и хорошее введение в
более существенные системы будут разработаны позже в этой главе.]
Раздел 2.4.2 покажет, как можно сделать оба представления.
сосуществовать в одной системе за счет использования тегов типов и общих
операции. 92 = -1$) можно рассматривать как точку в
плоскость, действительная координата которой $x$, а мнимая координата
$у$. Добавление комплексных чисел приводит в этом представлении к
добавление координат:
Вот почему пример комплексного числа
нереально. Тем не менее, это дает четкую иллюстрацию
проектирование системы с использованием общих операций и хорошее введение в
более существенные системы будут разработаны позже в этой главе.]
Раздел 2.4.2 покажет, как можно сделать оба представления.
сосуществовать в одной системе за счет использования тегов типов и общих
операции. 92 = -1$) можно рассматривать как точку в
плоскость, действительная координата которой $x$, а мнимая координата
$у$. Добавление комплексных чисел приводит в этом представлении к
добавление координат:
При умножении комплексных чисел более естественно мыслить терминами представления комплексного числа в полярной форме, как величина и угол. Произведение двух комплексных чисел — это вектор, полученный растягивая одно комплексное число на длину другого, а затем поворот его на угол другого:
Таким образом, комплексные числа могут быть представлены двумя разными способами.
которые подходят для разных операций. Тем не менее, из
точки зрения человека, пишущего программу, использующую комплексные числа,
принцип абстракции данных предполагает, что все операции для
манипулирование комплексными числами должно быть доступно независимо от того,
представление используется компьютером. Например, часто
полезно уметь определять действительную часть комплексного числа,
задается полярными координатами.
Тем не менее, из
точки зрения человека, пишущего программу, использующую комплексные числа,
принцип абстракции данных предполагает, что все операции для
манипулирование комплексными числами должно быть доступно независимо от того,
представление используется компьютером. Например, часто
полезно уметь определять действительную часть комплексного числа,
задается полярными координатами.
Для разработки такой системы мы можем следовать той же абстракции данных
стратегии, которой мы следовали при разработке пакета рациональных чисел. Предполагать
что операции над комплексными числами реализуются в терминах
четыре селектора: реальная часть , часть изображения , величина и угол .
Также предположим, что у нас есть две процедуры построения сложных
числа: make-from-real-imag возвращает комплексное число с указанным
действительная и мнимая части, и make-from-mag-ang возвращает комплекс
число с заданной величиной и углом. Эти процедуры имеют
свойство, что для любого комплексного числа
Эти процедуры имеют
свойство, что для любого комплексного числа z оба
(создать из реального изображения (реальная часть z) (часть изображения z))
и
(сделать-из-mag-ang (величина z) (угол z))
производят комплексные числа, равные z .
Используя эти конструкторы и селекторы, мы можем реализовать арифметику на комплексные числа с использованием «абстрактных данных», указанных конструкторами и селекторы. Как показано в формулах выше, мы можем складывать и вычитать комплексные числа по действительным и мнимым частям при умножении и деление комплексных чисел на величины и углы:
(определить (добавить-комплекс z1 z2)
(сделать из реального изображения (+ (реальная часть z1) (реальная часть z2))
(+ (часть изображения z1) (часть изображения z2))))
(определить (подкомплекс z1 z2)
(сделать из реального изображения (- (реальная часть z1) (реальная часть z2))
(- (часть изображения z1) (часть изображения z2))))
(определить (mul-complex z1 z2)
(сделать из реального изображения (* (величина z1) (величина z2))
(+ (угол z1) (угол z2))))
(определить (div-complex z1 z2)
(сделать из реального изображения (/ (величина z1) (величина z2))
(- (угол z1) (угол z2)))) Чтобы завершить пакет комплексных чисел, мы должны выбрать
представление, и мы должны реализовать конструкторы и селекторы в
с точки зрения примитивных чисел и примитивной структуры списка. Есть два
очевидные способы сделать это: мы можем представить комплексное число в
«прямоугольной формы» в виде пары или в «полярной форме» в виде пары.
Есть два
очевидные способы сделать это: мы можем представить комплексное число в
«прямоугольной формы» в виде пары или в «полярной форме» в виде пары.
Чтобы конкретизировать различные варианты выбора, представьте, что существует два программиста, Бем Битдиддл и Алисса П. Хакер, которые самостоятельно разрабатывать представления для комплексной системы счисления. Бен предпочитает представлять комплексные числа в прямоугольной форме. С этот выбор, выбирая действительную и мнимую части комплекса число просто, как и построение комплексного числа с Даны действительная и мнимая части. Чтобы найти величину и угол, или построить комплексное число с заданной величиной и углом, он использует тригонометрические соотношения
[Упомянутая здесь функция арктангенса, вычисленная с помощью схемы и процедура определена так, что tp принимает два аргумента $y$ и $x$ и
вернуть угол, тангенс которого равен $y/x$.]
, которые связывают действительную и мнимую части с величиной и углом. Таким образом, представление Бена задается следующими селекторами и
конструкторы:
Таким образом, представление Бена задается следующими селекторами и
конструкторы:
(определить (действительная часть z) (автомобиль z)) (определить (изображение-часть z) (cdr z)) (определить (величина z) (sqrt (+ (квадрат (действительная часть z)) (квадрат (изображение-часть z))))) (определить (угол z) (атан (имаг-часть z) (реальная часть z))) (определить (сделать из реального изображения x y) (против x y)) (определить (сделать-из-маг-анг р а) (cons (*r (cos a)) (*r (sin a))))
Алисса, напротив, предпочитает представлять комплексные числа в полярной форме. форма. Для нее выбор величины и угла прост, но она должна использовать тигонометрические отношения, чтобы получить реальный и мнимые части. Представительство Алисы:
(определить (действительная часть z)
(* (величина z) (cos (угол z))))
(определить (изображение-часть z)
(* (величина z) (sin (угол z))))
(определить (величина z) (автомобиль z))
(определить (угол z) (cdr z))
(определить (сделать из реального изображения x y)
(минусы (sqrt (+ (квадрат x) (квадрат y)))
(атан у х)))
(определить (сделать-из-mag-ang r a) (cons r a)) Дисциплина абстракции данных гарантирует, что один и тот же
реализация арифметических операций будет работать либо с
Представление Бена или представление Алиссы.
2.4.2 Тегированные данные
Одним из способов просмотра абстракции данных является приложение «принцип наименьшего обязательства». При реализации комплексного числа системы в разделе 2.4.1, мы можем использовать либо систему Бена прямоугольное представление или полярное представление Алиссы. барьер абстракции, образованный селекторами и конструкторами нам отложить до последнего момента выбор конкретного представление для наших объектов данных и, таким образом, сохранить максимальное гибкость в дизайне нашей системы.
Принцип наименьшего обязательства можно распространить и дальше.
крайности. Если мы захотим, мы можем сохранить двусмысленность
представление даже после того, как мы разработали селекторы и
конструкторы и выбрать использование представления Бена и Алиссы.
Однако если оба представления включены в единую систему, мы
потребуется какой-то способ отличить данные в полярной форме от данных в
прямоугольная форма. Простой способ добиться этого различия
должен включать тег типа – символ прямоугольный или полярный –
как часть каждого комплексного числа. Затем, когда нам нужно манипулировать
комплексное число, мы можем использовать тег, чтобы решить, какой селектор применить.
Затем, когда нам нужно манипулировать
комплексное число, мы можем использовать тег, чтобы решить, какой селектор применить.
Чтобы манипулировать тегированными данными, мы будем считать, что у нас есть
процедуры тег типа и содержимое , которые извлекаются из объекта данных
тег и актуальное содержимое. Мы также постулируем процедуру attach-tag , который принимает тег и содержимое и создает тегированные данные
объект. Простой способ реализовать это — использовать обычные
структура списка:
(определить (содержимое тега типа прикрепить)
(содержимое минус-тегов))
(определить (данные тега типа)
(если (пара? данные)
(данные автомобиля)
(ошибка "Датум с неверным тегом - TYPE-TAG" датум)))
(определить (данные содержания)
(если (пара? данные)
(данные CDR)
(ошибка "Датум с неверным тегом - СОДЕРЖИМОЕ" датум))) Используя эти процедуры, мы можем определить предикаты прямоугольные? и полярный? , которые распознают прямоугольные и полярные числа соответственно:
(определить (прямоугольный? z) (eq? (тип-тег z) 'прямоугольный)) (определить (полярный? г) (eq? (тип-тег z) 'полярный))
С помощью тегов type Бен и Алисса теперь могут изменять свой код, чтобы их
два разных представления могут сосуществовать в одной и той же системе. Когда бы ни
Бен строит комплексное число, помечает его как прямоугольное. Когда бы ни
Алиса составляет комплексное число и помечает его как полярное. Кроме того,
Бен и Алисса должны убедиться, что имена их процедур
не конфликт. Один из способов сделать это для Бена — добавить суффикс
Когда бы ни
Бен строит комплексное число, помечает его как прямоугольное. Когда бы ни
Алиса составляет комплексное число и помечает его как полярное. Кроме того,
Бен и Алисса должны убедиться, что имена их процедур
не конфликт. Один из способов сделать это для Бена — добавить суффикс прямоугольный на имя каждой из его процедур представления
и для Алиссы добавить полярный на ее имена. Вот это Бен
исправленное прямоугольное представление:
(определить (реальная часть-прямоугольная z) (автомобиль z))
(определить (изображение-часть-прямоугольный z) (cdr z))
(определить (величина-прямоугольник z)
(sqrt (+ (квадрат (действительная часть-прямоугольная z))
(квадрат (изображение-часть-прямоугольник z)))))
(определить (угол-прямоугольник z)
(атан (изображение-часть-прямоугольник z)
(реальная часть-прямоугольная z)))
(определить (сделать-из-реального-изображения-прямоугольным x y)
(прикрепить тег 'прямоугольный (минусы x y)))
(определить (сделать-из-mag-ang-прямоугольный r a)
(прикрепить тег 'прямоугольный
(cons (*r (cos a)) (*r (sin a))))) , а вот исправленное полярное представление Алиссы:
(определить (действительно-частично-полярный z)
(* (величина-поляра z) (cos (угол-поляра z))))
(определить (imag-part-polar z)
(* (величина-поляра z) (sin (угол-поляра z))))
(определить (величина-полярная z) (автомобиль z))
(определить (угол-полярный z) (cdr z))
(определить (сделать-из-реального-изображения-полярного x y)
(прикрепить тег «полярный
(минусы (sqrt (+ (квадрат x) (квадрат y)))
(атан у х))))
(определить (сделать-из-mag-ang-polar r a)
(attach-tag 'polar (cons r a))) Каждый общий селектор реализован как процедура, проверяющая
тег своего аргумента и вызывает соответствующую процедуру для обработки
данные такого типа. Например, чтобы получить действительную часть комплекса
число,
Например, чтобы получить действительную часть комплекса
число, реальная часть проверяет тег, чтобы определить, подходит ли нам Бен вещественно-частично-прямоугольный или Алиссы вещественно-частично-полярный . В любом случае,
мы используем содержимое для извлечения голых, непомеченных данных и отправки их в
прямоугольная или полярная процедура по мере необходимости:
(определить (действительная часть z)
(конд((прямоугольный?з)
(вещественно-прямоугольная часть (содержимое z)))
((полярный? г)
(вещественно-частично-полярный (содержимое z)))
(иначе (ошибка "Неизвестный тип - REAL-PART" z))))
(определить (изображение-часть z)
(конд((прямоугольный?з)
(imag-part-rectangular (содержимое z)))
((полярный? г)
(imag-part-polar (содержимое z)))
(иначе (ошибка "Неизвестный тип - IMAG-PART" z))))
(определить (величина z)
(конд((прямоугольный?з)
(величина-прямоугольная (содержимое z)))
((полярный? г)
(величина-полярная (содержимое z)))
(иначе (ошибка "Неизвестный тип - ВЕЛИЧИНА" z))))
(определить (угол z)
(конд((прямоугольный?з)
(угол-прямоугольный (содержимое z)))
((полярный? г)
(угол-полярный (содержимое z)))
(еще (ошибка "Неизвестный тип - ANGLE" z)))) Для реализации комплексно-арифметических операций можно использовать тот же
процедуры, потому что селекторы, которые они вызывают, являются общими, и поэтому
работать с любым представлением.
Наконец, мы должны решить, строить ли комплексные числа, используя
Представление Бена или представление Алиссы. Один разумный выбор
заключается в построении прямоугольных чисел всякий раз, когда у нас есть действительные и
мнимые части и строить полярные числа всякий раз, когда у нас есть
величины и углы:
(определить (сделать из реального изображения x y)
(сделать-из-реального-образа-прямоугольным x y))
(определить (сделать-из-маг-анг р а)
(сделать-из-mag-ang-polar r a)) Полученная система комплексных чисел была разбита на три
относительно независимые части: комплексно-числовые арифметические операции,
Полярная реализация Алисы и прямоугольная реализация Бена.
Полярные и прямоугольные реализации могли быть написаны
Бен и Алисса работают отдельно, и оба они могут использоваться как
базовые представления третьим программистом, реализующим
комплексно-арифметические процедуры в терминах абстрактного
интерфейс конструктора/селектора.
Поскольку каждый объект данных помечен тегом своего типа, селекторы работают
на данные в общем виде. То есть каждый селектор определяется как
иметь поведение, которое зависит от конкретного типа данных
применительно к. Обратите внимание на общий механизм взаимодействия отдельных
представления: в рамках данной реализации представления (скажем,
полярный пакет Алисы) комплексное число представляет собой нетипизированную пару (величина,
угол). Когда универсальный селектор работает с числом
То есть каждый селектор определяется как
иметь поведение, которое зависит от конкретного типа данных
применительно к. Обратите внимание на общий механизм взаимодействия отдельных
представления: в рамках данной реализации представления (скажем,
полярный пакет Алисы) комплексное число представляет собой нетипизированную пару (величина,
угол). Когда универсальный селектор работает с числом полярных 9тип 0923,
он срывает метку и передает содержимое коду Алиссы.
И наоборот, когда Алисса составляет номер для общего пользования, она помечает
с типом, чтобы он мог быть надлежащим образом распознан
процедуры более высокого уровня. Эта дисциплина раздевания и
прикрепление тегов по мере того, как объекты данных передаются с уровня на уровень, может быть
важная организационная стратегия, как мы увидим в
Раздел 2.5
2.4.3 Программирование, управляемое данными, и аддитивность
2.4.3 Программирование, управляемое данными, и аддитивность Общая стратегия проверки типа данных и вызова
соответствующая процедура называется диспетчерская по типу . Это
мощная стратегия для достижения модульности в проектировании системы. На
с другой стороны, реализуя отправку, как в разделе 2.4.2.
имеет два существенных недостатка. Одним из недостатков является то, что общий
процедуры интерфейса должны знать обо всех различных представлениях.
Например, предположим, что мы хотим включить новое представление
для комплексных чисел в нашу систему комплексных чисел. Нам нужно
идентифицируйте это новое представление с типом, а затем добавьте предложение в
каждой из общих процедур интерфейса для проверки нового типа и
применить соответствующий селектор для этого представления.
Это
мощная стратегия для достижения модульности в проектировании системы. На
с другой стороны, реализуя отправку, как в разделе 2.4.2.
имеет два существенных недостатка. Одним из недостатков является то, что общий
процедуры интерфейса должны знать обо всех различных представлениях.
Например, предположим, что мы хотим включить новое представление
для комплексных чисел в нашу систему комплексных чисел. Нам нужно
идентифицируйте это новое представление с типом, а затем добавьте предложение в
каждой из общих процедур интерфейса для проверки нового типа и
применить соответствующий селектор для этого представления.
Еще одна слабость метода заключается в том, что, хотя
представления могут быть разработаны отдельно, мы должны гарантировать, что никакие
две процедуры во всей системе имеют одно и то же имя. Вот почему
Бену и Алиссе пришлось изменить названия своих первоначальных процедур.
из раздела 2.4.1.
Проблема, лежащая в основе обоих этих недостатков, заключается в том, что метод
для реализации универсальных интерфейсов не является дополнением . Персона
реализация общих селекторных процедур должна изменить те
процедуры каждый раз, когда устанавливается новое представительство, и люди
интерфейс отдельных представлений должен изменить их код, чтобы
избегать конфликтов имен. В каждом из этих случаев изменения, которые должны быть
внесены в код, просты, но они должны быть сделаны
тем не менее, и это является источником неудобств и ошибок. Это
не большая проблема для системы комплексных чисел в ее нынешнем виде, но
предположим, что было не два, а сотни различных представлений
для комплексных чисел. И предположим, что было много общих
селекторы, которые должны поддерживаться в интерфейсе абстрактных данных. Предположим, в
факт, что ни один программист не знал всех интерфейсных процедур всех
представления. Проблема реальна и должна решаться в
программы как крупномасштабные системы управления базами данных.
Персона
реализация общих селекторных процедур должна изменить те
процедуры каждый раз, когда устанавливается новое представительство, и люди
интерфейс отдельных представлений должен изменить их код, чтобы
избегать конфликтов имен. В каждом из этих случаев изменения, которые должны быть
внесены в код, просты, но они должны быть сделаны
тем не менее, и это является источником неудобств и ошибок. Это
не большая проблема для системы комплексных чисел в ее нынешнем виде, но
предположим, что было не два, а сотни различных представлений
для комплексных чисел. И предположим, что было много общих
селекторы, которые должны поддерживаться в интерфейсе абстрактных данных. Предположим, в
факт, что ни один программист не знал всех интерфейсных процедур всех
представления. Проблема реальна и должна решаться в
программы как крупномасштабные системы управления базами данных.
Нам нужно средство для модульного проектирования системы даже
дальше. Это обеспечивается методом программирования, известным как программирование, управляемое данными . Чтобы понять, как
программирование работает, начните с наблюдения, что всякий раз, когда мы имеем дело
с набором общих операций, которые являются общими для набора различных
типов мы, по сути, имеем дело с двумерной таблицей, которая
содержит возможные операции на одной оси и возможные типы на
другая ось. Записи в таблице — это процедуры, которые
реализовать каждую операцию для каждого типа представленного аргумента. в
система комплексных чисел, разработанная в предыдущем разделе,
соответствие между именем операции, типом данных и фактической процедурой
был разбросан среди различных условных предложений в общем
процедуры интерфейса. Но та же самая информация может быть организована в
стол:
Чтобы понять, как
программирование работает, начните с наблюдения, что всякий раз, когда мы имеем дело
с набором общих операций, которые являются общими для набора различных
типов мы, по сути, имеем дело с двумерной таблицей, которая
содержит возможные операции на одной оси и возможные типы на
другая ось. Записи в таблице — это процедуры, которые
реализовать каждую операцию для каждого типа представленного аргумента. в
система комплексных чисел, разработанная в предыдущем разделе,
соответствие между именем операции, типом данных и фактической процедурой
был разбросан среди различных условных предложений в общем
процедуры интерфейса. Но та же самая информация может быть организована в
стол:
| Полярный | Прямоугольный
-------------------------------------------------- ---
реальная часть | вещественно-частично-полярный | реальная часть прямоугольная
часть изображения | изображение-частично-полярный | часть изображения прямоугольная
величина | величина-полярная | величина-прямоугольный
угол | угловой полярный | углово-прямоугольный
Для реализации этого плана предположим, что у нас есть две процедуры, поставить и получить , для работы с таблицей операций и типов:
(поместитеустанавливает- )
(getищет)  Если элемент не найден,
Если элемент не найден, возвращает. ложь
Пока можно считать, что поставили , а получили включены в наш
язык. В
Глава 3 (раздел 3.3.3)
мы увидим, как реализовать эти и другие операции для
манипуляции с таблицами.
Вот как программирование, управляемое данными, можно использовать в комплексе
система счисления. Бен, разработавший прямоугольное представление,
реализует свой код так же, как и изначально. Он определяет коллекцию
процедур или пакет и связывает их с остальными
систему, добавляя записи в таблицу, которые сообщают системе, как
работать с прямоугольными числами. Это достигается вызовом
следующая процедура:
(определить (установить прямоугольный пакет)
;; внутренние процедуры
(определить (реальная часть z) (автомобиль z))
(определить (изображение-часть z) (cdr z))
(определить (сделать из реального изображения x y) (против x y))
(определить (величина z)
(sqrt (+ (квадрат (действительная часть z))
(квадрат (изображение-часть z)))))
(определить (угол z)
(атан (имаг-часть z) (реальная часть z)))
(определить (сделать-из-маг-анг р а)
(cons (*r (cos a)) (*r (sin a))))
;; интерфейс к остальной части системы
(определить (тег x) (прикрепить-тег 'прямоугольный x))
(поместите 'действительную часть' (прямоугольную) действительную часть)
(поместите 'imag-part' (прямоугольную) imag-part)
(поместите «величину» (прямоугольную) величину)
(поставить 'угол' (прямоугольный) угол)
(поставьте 'сделать из реального изображения' прямоугольный
(лямбда (x y) (тег (сделать из реального изображения x y))))
(поместите 'сделать из-mag-ang' прямоугольный
(лямбда (r a) (тег (make-from-mag-ang r a))))
готово) Обратите внимание, что внутренние процедуры здесь те же процедуры, что и в
Раздел 2. 4.1, который Бен написал, когда работал в
изоляция. Никаких изменений не требуется, чтобы связать их с
остальная часть системы. Более того, поскольку эти определения процедур
внутри процедуры установки, Бену не нужно беспокоиться об имени
конфликтов с другими процедурами вне прямоугольного пакета. К
связать их с остальной системой, Бен устанавливает свою
4.1, который Бен написал, когда работал в
изоляция. Никаких изменений не требуется, чтобы связать их с
остальная часть системы. Более того, поскольку эти определения процедур
внутри процедуры установки, Бену не нужно беспокоиться об имени
конфликтов с другими процедурами вне прямоугольного пакета. К
связать их с остальной системой, Бен устанавливает свою реальную часть процедура под именем операции реальная часть и тип (прямоугольный) и аналогично для других селекторов. [Мы используем
список (прямоугольный) , а не символ прямоугольный , чтобы учесть
возможность операций с несколькими аргументами, а не всеми
того же типа.] Интерфейс также определяет конструкторы, которые будут использоваться
внешняя система. [Тип, под которым устанавливаются конструкторы
не обязательно должен быть списком, потому что конструктор всегда используется для создания
объекты одного определенного типа.] Они идентичны объектам Бена.
внутренне определенные конструкторы, за исключением того, что они присоединяют тег.
Полярный пакет Алисы аналогичен:
(определить (установить полярный пакет)
;; внутренние процедуры
(определить (величина z) (автомобиль z))
(определить (угол z) (cdr z))
(определить (сделать-из-mag-ang r a) (cons r a))
(определить (действительную часть z)
(* (величина z) (cos (угол z))))
(определить (изображение-часть z)
(* (величина z) (sin (угол z))))
(определить (сделать из реального изображения x y)
(минусы (sqrt (+ (квадрат x) (квадрат y)))
(атан у х)))
;; интерфейс к остальной части системы
(определить (тег x) (прикрепить тег 'полярный x))
(поставьте «реальная часть» (полярная) реальная часть)
(поместите 'imag-part' (полярный) imag-part)
(поставьте «величину» (полярную) величину)
(поставьте 'угол' (полярный) угол)
(поставьте «сделать из реального изображения» полярный
(лямбда (x y) (тег (сделать из реального изображения x y))))
(поставьте «сделать из-mag-ang» полярный
(лямбда (r a) (тег (make-from-mag-ang r a))))
готово) Несмотря на то, что Бен и Алисса по-прежнему используют свои первоначальные процедуры
определения с теми же именами, что и друг у друга, эти определения теперь
внутренние по отношению к разным процедурам, поэтому конфликта имен нет.
Комплексно-арифметические селекторы обращаются к таблице с помощью
общая процедура «операции», называемая apply-generic , которая применяет
общая операция для некоторых аргументов. Apply-generic смотрит в
таблица по названию операции и типам аргументов
и применяет результирующую процедуру, если она присутствует:
(определить (apply-generic op. args)
(let ((тип-теги (аргументы тега типа карты)))
(let ((proc (получить op type-tags)))
(если прок
(применить proc (аргументы содержимого карты))
(ошибка
"Нет метода для этих типов - APPLY-GENERIC"
(список тэгов оп))))) [ Apply-generic использует обозначение с точками, потому что разные
универсальные операции могут принимать разное количество аргументов. В apply-generic , op имеет в качестве значения первый аргумент для apply-generic и args имеет в качестве значения список оставшихся
аргументы.
Apply-generics также использует примитивную процедуру apply , которая
принимает два аргумента, процедуру и список. Применить применяет
процедура, использующая элементы списка в качестве аргументов. Например, (применить + (список 1 2 3 4)) возвращает 10.]
Используя apply-generic , мы можем определить наши общие селекторы следующим образом:0003
(определить (реальная часть z) (применить общий 'реальная часть z))
(определить (imag-part z) (apply-generic 'imag-part z))
(определить (величина z) (apply-generic 'величина z))
(определить (угол z) (применить общий угол z)) Обратите внимание, что они вообще не меняются, если появляется новое представление.
добавил в систему.
Мы также можем извлечь из таблицы конструкторы, которые будут использоваться
программ, внешних по отношению к пакетам, в создании комплексных чисел из действительных
и мнимых частей и от величин и углов.

 Например, теорема Ферма.
Например, теорема Ферма.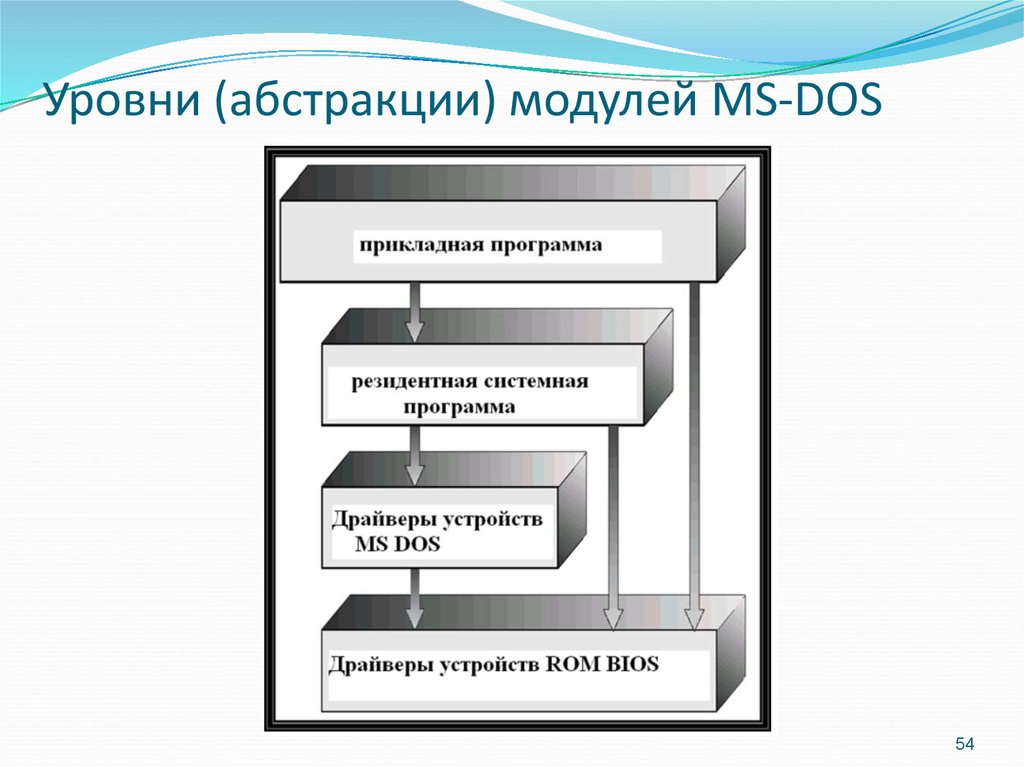 1. Отступление «об абстрагировании»
1. Отступление «об абстрагировании»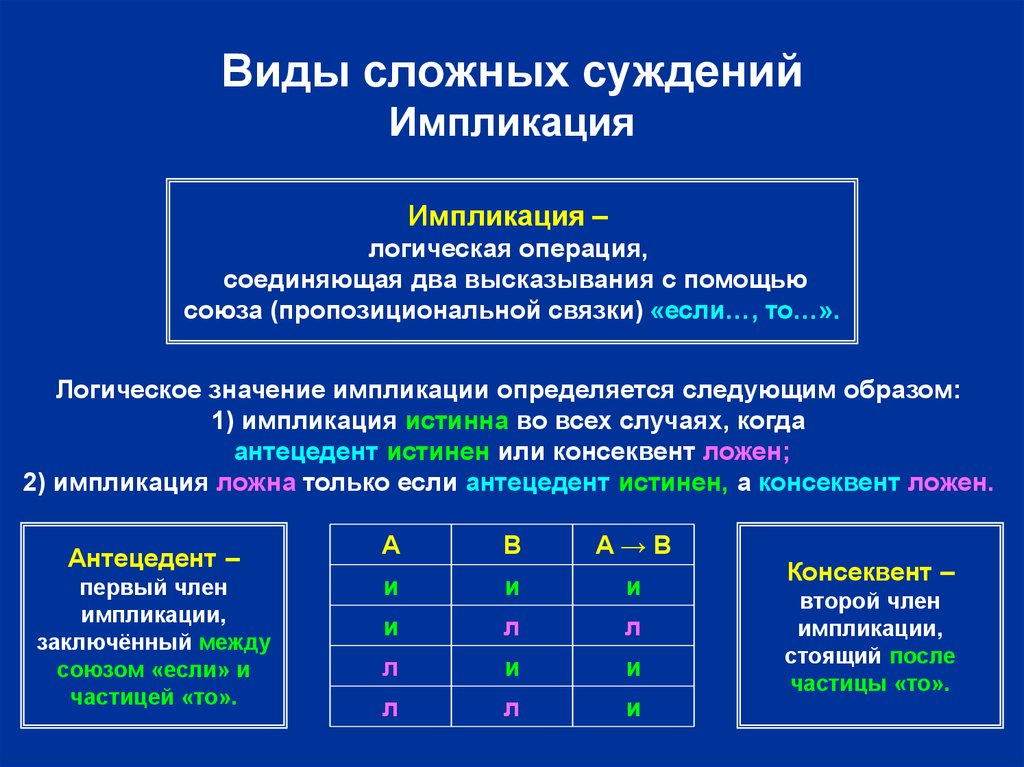

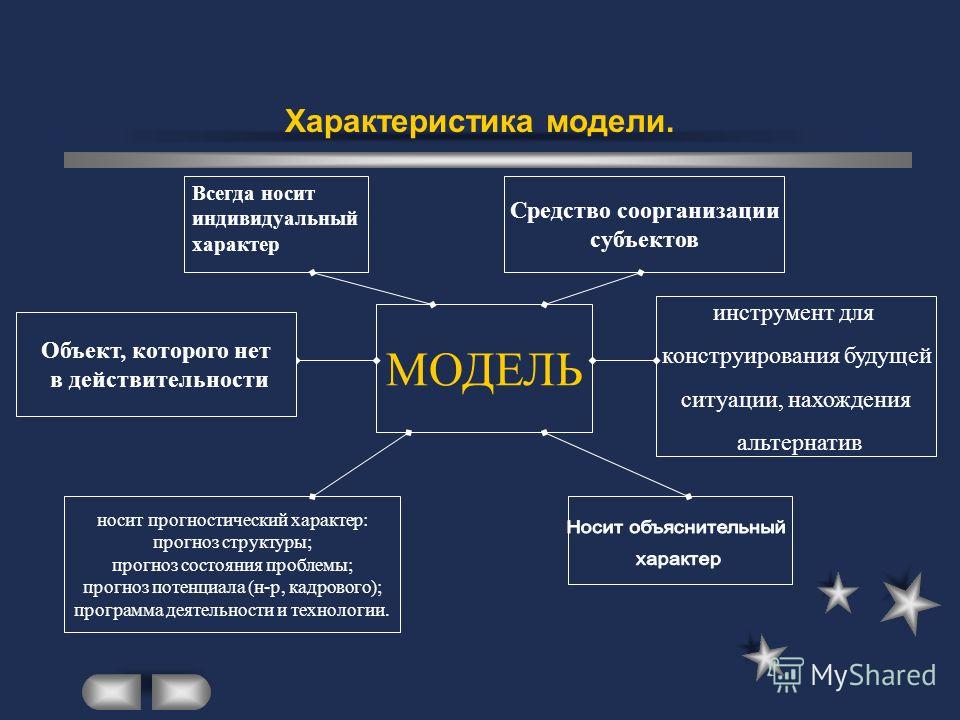 В
качестве первичного ключа берется ключ
одной из сущностей.
В
качестве первичного ключа берется ключ
одной из сущностей.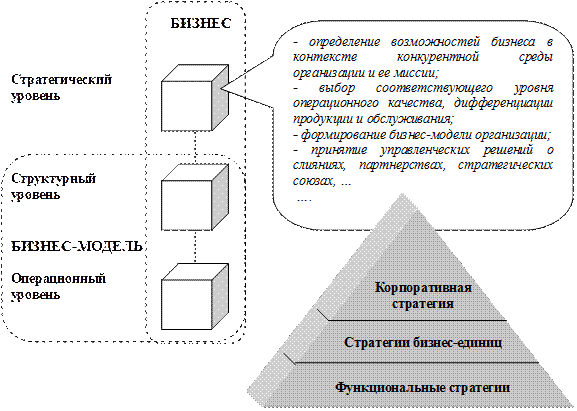
 real + other.real, self.imag + other.imag)
def mul(я, другой):
величина = собственная величина * другая.величина
return ComplexMA (величина, собственный угол + другой угол)
real + other.real, self.imag + other.imag)
def mul(я, другой):
величина = собственная величина * другая.величина
return ComplexMA (величина, собственный угол + другой угол)
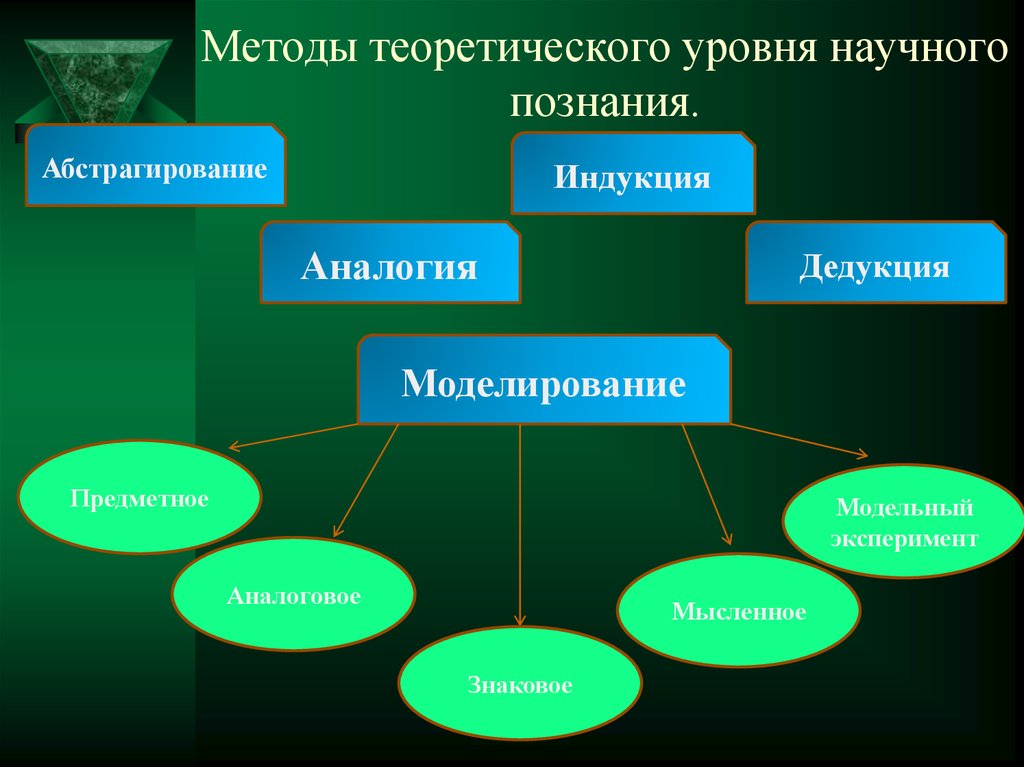 magnitude * cos(self.angle)
@имущество
деф образ(я):
вернуть self.magnitude * sin(self.angle)
защита __repr__(сам):
return 'ComplexMA({0:g}, {1:g} * pi)'.format(self.magnitude, self.angle/pi)
magnitude * cos(self.angle)
@имущество
деф образ(я):
вернуть self.magnitude * sin(self.angle)
защита __repr__(сам):
return 'ComplexMA({0:g}, {1:g} * pi)'.format(self.magnitude, self.angle/pi)
 type_tag) в self.adders:
вернуть self.cross_apply (другое, self.adders)
def __mul__(я, другой):
если self.type_tag == other.type_tag:
вернуть self.mul(другое)
elif (self.type_tag, other.type_tag) в self.multipliers:
вернуть self.cross_apply (другое, self.multipliers)
def cross_apply (я, другой, cross_fns):
cross_fn = cross_fns[(self.type_tag, other.type_tag)]
вернуть cross_fn(я, другой)
adders = {("ком", "крыса"): add_complex_and_rational,
("крыса", "com"): add_rational_and_complex}
multipliers = {("com", "rat"): mul_complex_and_rational,
("крыса", "ком"): mul_rational_and_complex}
type_tag) в self.adders:
вернуть self.cross_apply (другое, self.adders)
def __mul__(я, другой):
если self.type_tag == other.type_tag:
вернуть self.mul(другое)
elif (self.type_tag, other.type_tag) в self.multipliers:
вернуть self.cross_apply (другое, self.multipliers)
def cross_apply (я, другой, cross_fns):
cross_fn = cross_fns[(self.type_tag, other.type_tag)]
вернуть cross_fn(я, другой)
adders = {("ком", "крыса"): add_complex_and_rational,
("крыса", "com"): add_rational_and_complex}
multipliers = {("com", "rat"): mul_complex_and_rational,
("крыса", "ком"): mul_rational_and_complex}



 коэффициенты
Выход[8]: (0, 1, 2)
коэффициенты
Выход[8]: (0, 1, 2)
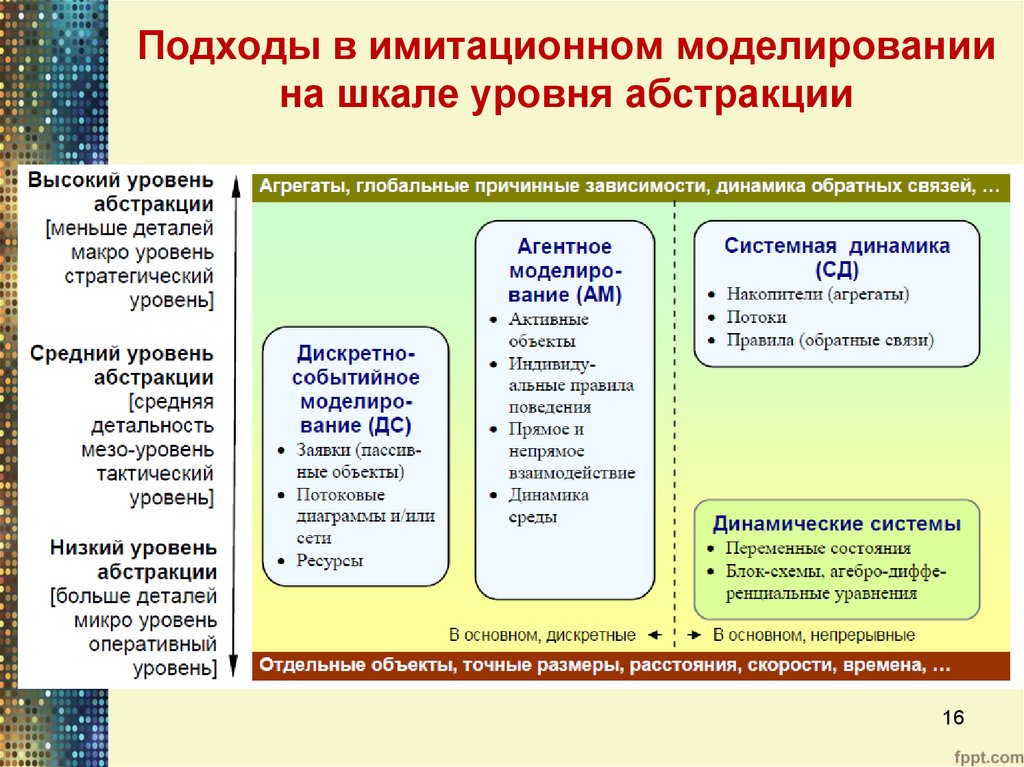 коэффициенты = коэфф.
Степень защиты (я):
вернуть len (собственные.коэффициенты) - 1
коэффициенты = коэфф.
Степень защиты (я):
вернуть len (собственные.коэффициенты) - 1
 , 1+0j, 'f')
Выход[3]: Истина
В [4]: (0, 1, "f") == (0., 1+0j, 'g')
Выход[4]: Ложь
В [5]: (0, 1, "f") == (0., 1+0j)
Выход[5]: Ложь
, 1+0j, 'f')
Выход[3]: Истина
В [4]: (0, 1, "f") == (0., 1+0j, 'g')
Выход[4]: Ложь
В [5]: (0, 1, "f") == (0., 1+0j)
Выход[5]: Ложь
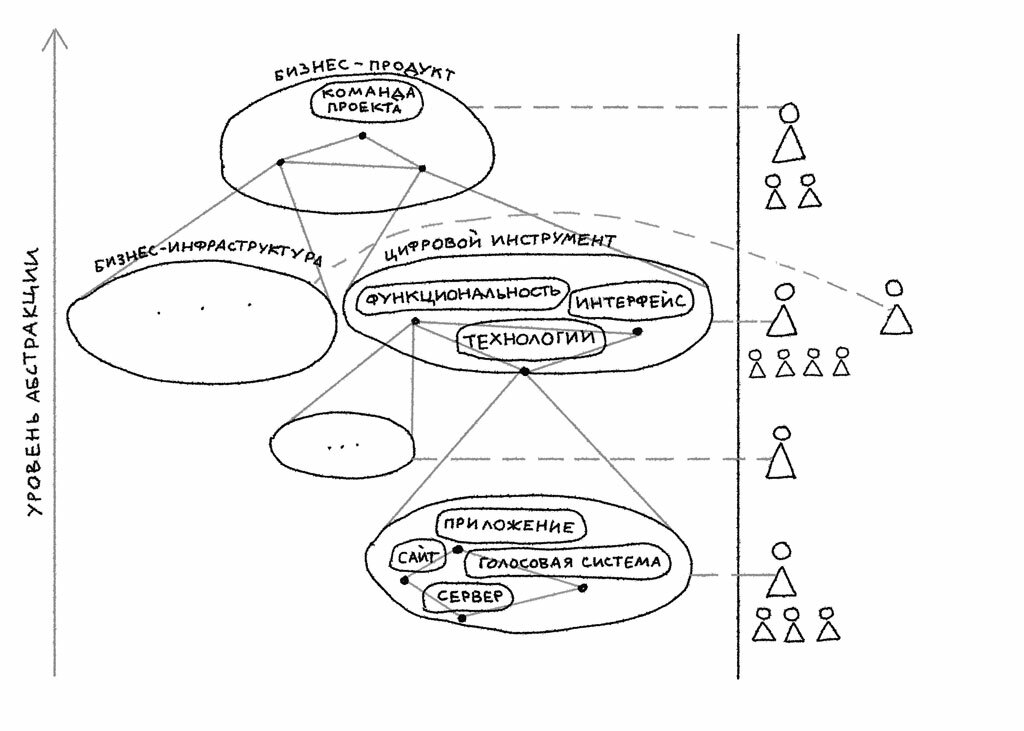 coefficients [: common],
12 других.коэффициентов[:общие]))
13
14 # Добавляем коэффициенты старшей степени из старшей степени
15 # слагаемое.
16 коэффициентов += собственные.коэффициенты[общие:] + другие.коэффициенты[общие:]
17
18 обратных полиномов (коэффициенты)
193 + 2x + 2
В [8]: print(1 + a)
-------------------------------------------------- -------------------------
TypeError Traceback (последний последний вызов)
coefficients [: common],
12 других.коэффициентов[:общие]))
13
14 # Добавляем коэффициенты старшей степени из старшей степени
15 # слагаемое.
16 коэффициентов += собственные.коэффициенты[общие:] + другие.коэффициенты[общие:]
17
18 обратных полиномов (коэффициенты)
193 + 2x + 2
В [8]: print(1 + a)
-------------------------------------------------- -------------------------
TypeError Traceback (последний последний вызов)