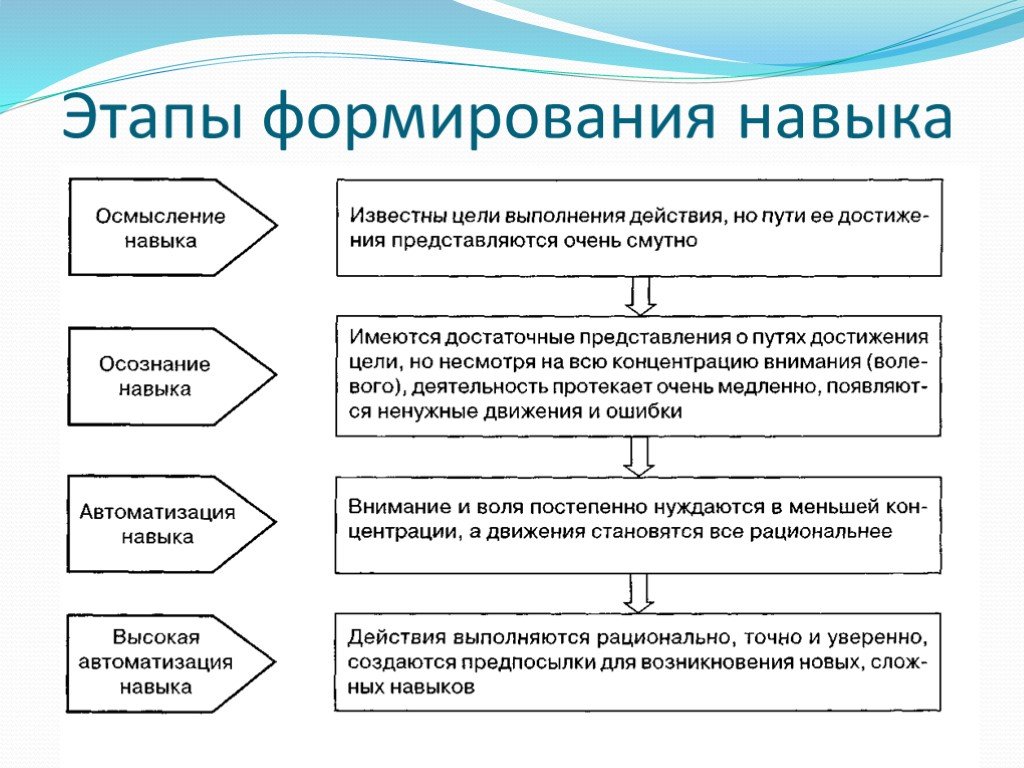
Основные этапы процесса мышления
15.05.2012
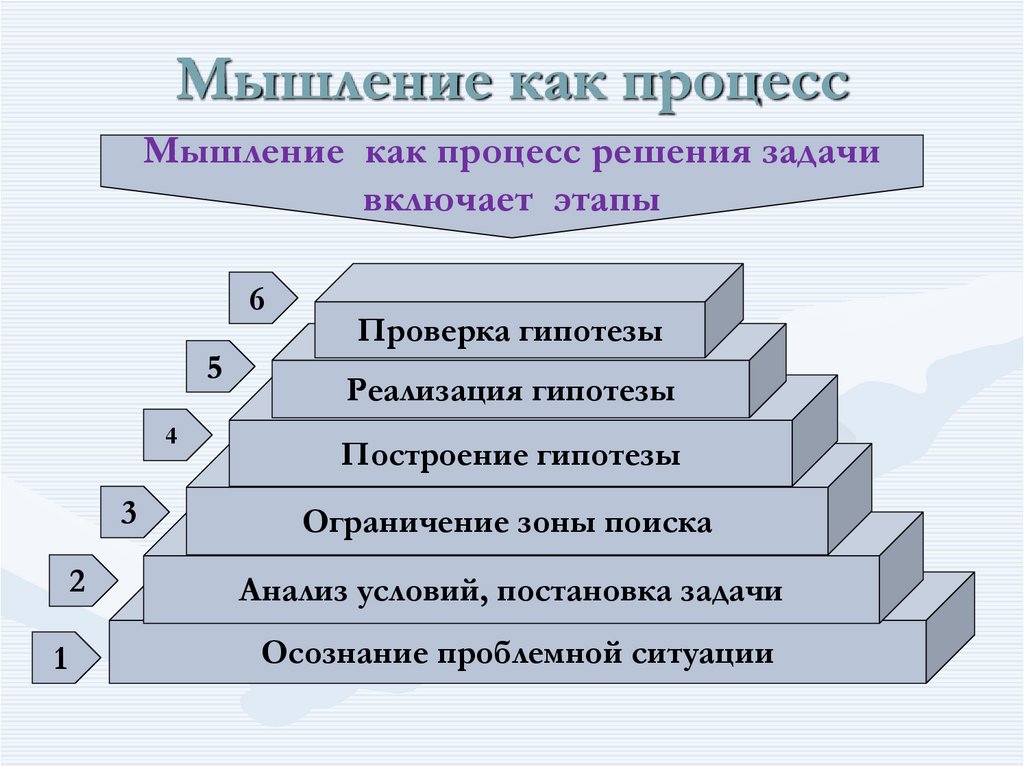
В ходе решения сложной задачи можно выделить несколько основных этапов процесса мышления.
1. Начало мыслительного процесса состоит в осознании проблемной ситуации. Уже этот этап оказывается не всем под силу — тот, кто не привык мыслить, воспринимает окружающий мир как само собой разумеющееся. Чем больше знаний, тем больше проблем видит человек. Необходимо иметь мышление И.Ньютона, чтобы увидеть в падающем на землю яблоке проблему.
В структуру проблемной ситуации входят познавательная потребность, побуждающая человека к деятельности; неизвестное достигаемое знание (т.е. предмет потребности) и интеллектуальные возможности человека.
2. Следующий этап мыслительного процесса состоит в формулировке задачи.
Это означает, что в данных условиях удалось предварительно расчленить известное (данное) и неизвестное (искомое), а также определить требование (цель).
3. Следующий этап мыслительного процесса — это разработка стратегии решения задачи, общей схемы решения.
Задача решается различными способами, выбор которых обусловлен условиями задачи и интеллектуальными возможностями субъекта. Если решаемая задача предполагает знание правил, то это означает включение в общую структуру еще двух этапов. На первом необходимо определить то правило, которое будет использовано, а на втором — применить данное общее правило к конкретным, частным условиям.
Способом решения задачи может быть алгоритм, эвристика, правила и т.д.
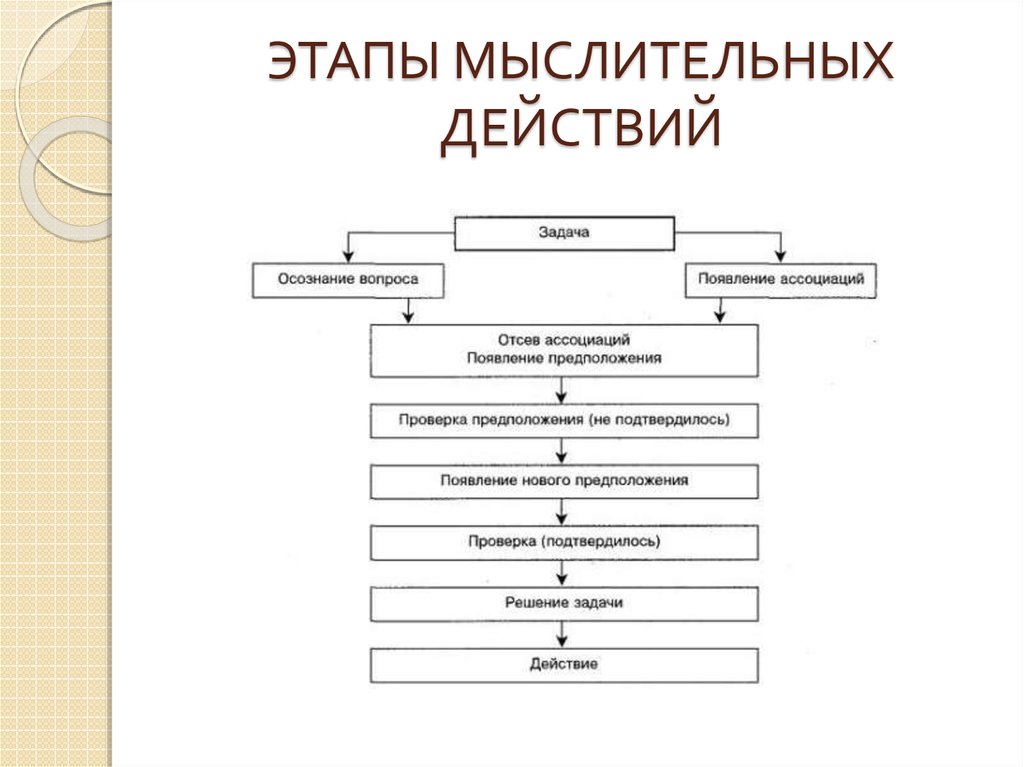
В ходе разработки общей схемы решения задачи появляется гипотеза или несколько гипотез, но возникают они не всегда последовательно, и на любом этапе мыслительного процесса. Существуют следующие способы выдвижения гипотез:
- сначала формулируются все возможные гипотезы, а затем в ходе проверки отбрасываются ложные;
- гипотезы выдвигаются и проверяются последовательно, по одной;
- в результате бессистемности действий (азарт) ни одна из гипотез не доводится до конца;
- гипотезы не формулируются, а идет поиск случайного решения.
4. Определив стратегию, переходят к выделению частных операций, последовательность которых необходимо строго соблюдать. Цепь последовательных операций приводит к определенному результату.
5. Последний этап мыслительного процесса — это сравнение результата с исходным условием. В том случае, если результат соответствует условию, задача считается решенной. Если же такого соответствия нет, действие начинается снова, пока нужное согласование результата с исходным условием не будет достигнуто.
Ключевые слова: Мышление
Источник: Кураев Г.А., Пожарская Е.Н., Психология человека
| Материалы по теме |
|---|
Личностные факторы мышления Саенко Ю.В., Общая психология. Часть 3 |
Механизмы мышления. … |
Сверхценные образования и паранойяльные состояния Справочник по психиатрии / Н.М. Жариков, Д.Ф. Хритинин, М.А. Лебедев. — М.: ООО «… |
Мышление: его виды и связь с языком Занковский А.Н., Психология деловых отношений |
Нарушение личностного компонента мышления Т. П. Пушкина Медицинская психология |
Классификация типов мышления Творогова Н.Д., Общая и социальная психология |
Общая характеристика мышления в современной психологии Константинов В.В., Основы общей психологии |
Факторы творческого мышления Саенко Ю.В., Общая психология. Часть 3 |
Метод картирования виутрикоркового взаимодействияТесты для контроля знаний
I.
Общие вопросы
методики преподавания математики
1. Процесс обучения математике является _________ методики преподавания математики.
2. Ядро методической системы обучения математике составляют цели, содержание, _______обучения.
3. Установите соответствие между названием учебно-методического комплекта и фамилией автора программы по математике.
1) Начальная школа ХХI века; 2) Планета знаний; 3) Школа 2000..; 4) Гармония;
5) Перспективная начальная школа; 6) Школа России.
а) Н.Б. Истомина; б) Л.Г. Петерсон в) В.Н. Рудницкая ;г) А.Л. Чекин, Л.П. Юдина и др.;
д) М.Г. Нефедова и др.; е) М.И. Моро и др.
4. Развивающая функция обучения математике заключается в :
1) совершенствовании вычислительной культуры младших школьников;
2) воспитании интереса к предмету; 3) развитии пространственного воображения;
4) становлении приемов умственной деятельности.
5. Задачи
обучения математике в дидактической системе Л.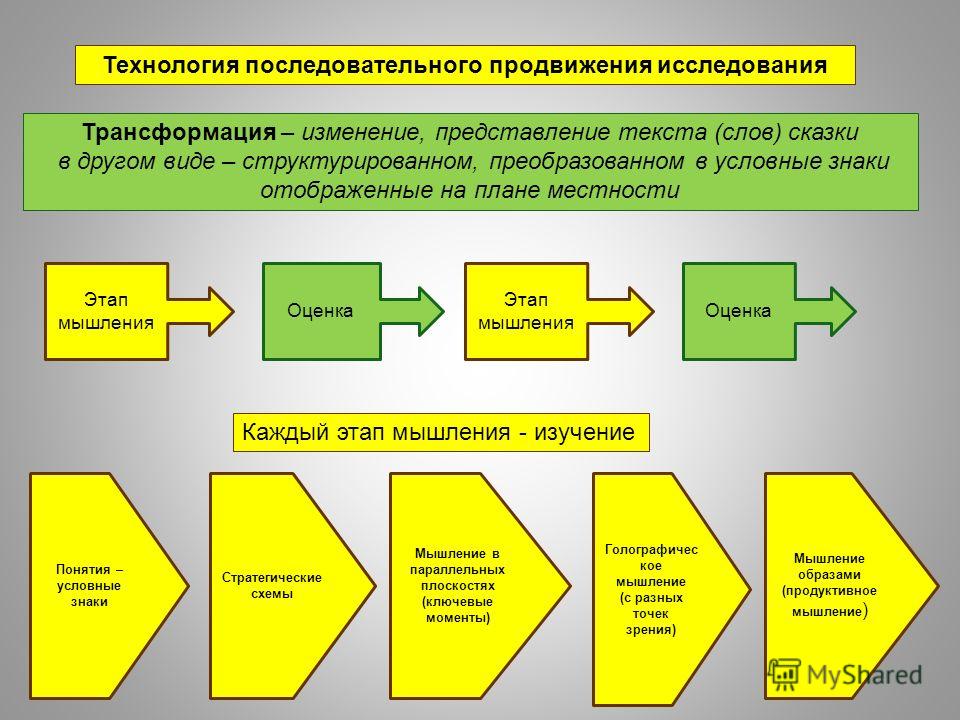
В. Занкова можно сформулировать
так:
1) способствовать продвижению учащихся в общем развитии;
2) формировать представление о математике как науке, обобщающей реально происходящие явления;
3) развивать алгоритмическое мышление школьников; 4) формировать конструкторские умения и навыки;
5) формировать знания, умения и навыки, необходимые для жизни и дальнейшего обучения.
6. Установите соответствие между понятием и компонентом содержания начального математического образования.
1) Дробные числа; 2) площадь 3) угол 4) равенство.
а) Величины; б) элементы геометрии; в) арифметический материал; г) элементы алгебры
д) элементы комбинаторики.
7. Данные суждения верны.
1) Внеклассная работа — это обязательные систематические занятия педагога с учащимися в свободное от основных занятий время.
2) Урок — это основная форма обучения младших школьников математике.
3) Занятия математического кружка способствуют
воспитанию у младших школьников интереса к математике.
4) К видам внеклассной работы относятся: домашняя работа учащихся, групповая работа, фронтальная работа.
5) Основными методами обучения младших школьников математике являются наблюдение и эксперимент.
8. Установите последовательность этапов урока открытия нового знания в структуре технологии деятельностного метода «Школа 2000…» (Л.Г. Петерсон).
1) Постановка учебной задачи. 2) Открытие нового знания. 3) Самостоятельная работа с самопроверкой.
4) Первичное закрепление. 5) Актуализация опорных знаний. 6) Итог урока (рефлексия).
7) Самоопределение к учебной деятельности. 8) Включение в систему знаний и повторение.
9. Тип и структура урока математики в начальной школе определяются:
1) дидактическими задачами урока; 2) воспитательными задачами урока; 3) индивидуальными особенностями младших школьников; 4) местом урока в расписании;
5) степенью освоения учащимися содержания
учебной темы.
10. Установите соответствие между этапом урока открытия нового знания и его дидактической целью.
1) Открытие нового знания. 2) Итог урока. 3) Организационный момент. 4) Актуализация опорных знаний. 5) Повторение. 6) Самостоятельная работа с самопроверкой.
а) Формирование навыков самоконтроля и самооценки; б) включение нового знания в систему знаний;
в) содержательная и мыслительная подготовка; г) положительное самоопределение к учебной деятельности;
д) рефлексия деятельности; е) проектирование и фиксация нового знания;
ж) изучение основного содержания учебной темы, формирование знаний, умений и навыков.
11. Домашняя работа по математике в начальной школе:
1) является формой самостоятельной работы учащихся; 2) выполняется учащимися по желанию;
3) подлежит обязательной проверке учителем или самопроверке;
4) содержит задания только занимательного
характера; 5) направлена на тренировку учащихся в известных способах действий.
12. Функциями учебника как основного средства обучения математики в начальной
школе являются: 1) занимательная; 2) воспитательная; 3) актуализирующая;
4) информирующая; 5) мотивирующая; 6) развивающая.
Ответы: Общие вопросы методики преподавания математики
1. Ответ: предметом.
2. Ответ: методы.
3. Ответ: 1в, 2д, 3б, 4а, 5г, 6е.
4. Ответ: 3, 4.
5. Ответ: 1, 2, 5.
6 Ответ: 1в, 2а, 3б, 4г.
7. Ответ: 2, 3.
8 Ответ: 7, 5, 1, 2, 4, 3, 8, 6.
9. Ответ: 1, 5.
10. Ответ: 1е, 2д, 3г, 4в, 5б, 6а.
11. Ответ: 1, 3, 5.
12. Ответ: 2, 4, 5, 6.
II Методика формирования у младших школьников вычислительной культуры
1.
Дидактические цели урока по теме «Название
и запись трехзначных чисел»
формулируются так:
1) формировать способность к чтению и записи трехзначных чисел;
2) формировать способность к выражению трехзначных чисел в разных единицах счета;
3) тренировать мыслительные операции обобщения, сравнения, анализа;
4) формировать умение складывать и вычитать трехзначные числа столбиком;
5) актуализировать знания об образовании, записи и сравнении двузначных чисел.
2. В программах Н.Б. Истоминой и И.И. Аргинской числа первого десятка изучаются не по порядку, а по принципу схожести и трудности написания цифр. Данный
подход предусматривает формирование:
1) порядкового натурального числа;
2) натурального числа как меры величин;
3) количественного натурального числа;
4) натурального числа как результата счета и измерения.
3. Задания арифметического диктанта на проверку знаний по теме «Нумерация трехзначных чисел» могут быть следующими:
1) увеличь число 300 на 28;
2) запиши число, которое больше 516 на 1;
3) запиши число, содержащее 32 сотни, 32 десятка и 32 единицы;
4) запиши все трехзначные четные числа при помощи цифр 5, 6 и 8;
5) уменьшаемое 739, вычитаемое 186, найди разность;
6) запиши число, содержащее 3 сотни, 25 десятков, 25 единиц.
4. На этапе постановки учебной задачи педагог предлагает учащимся сосчитать
предметы, группируя их сначала по 5, затем по 6, 7, и записать результат счета числом. После выполнения этого задания учащиеся сделают выводы:
1) результат счета зависит от единицы счета;
2) единица счета должна быть единой;
3) десяток — новая счетная единица;
4) нельзя считать группами по 5, по 6, по 7;
5) число, полученное в результате счета, не зависит от выбранной единицы счета.
5. Установите последовательность обучения младших школьников пересчету
предметов.
1) Пересчет изображений предметов, расположенных линейно.
2) Пересчет изображений предметов, расположенных хаотично.
3) Пересчет предметов и явлений, которые исчезают после воздействия на органы
чувств (хлопки, гудки, вспышки света).
4) Счет материальных объектов (счетных палочек, кубиков).
6. С целью дифференциации понятий число и цифра используются:
1) задания на составление чисел из заданных цифр;
2) знакомство с разными позиционными системами счисления;
3) знакомство с римской и славянской нумерацией;
4) изучение этимологии соответствующих слов;
5) работа с числовым отрезком, числа которого обозначены «волшебными»
цифрами.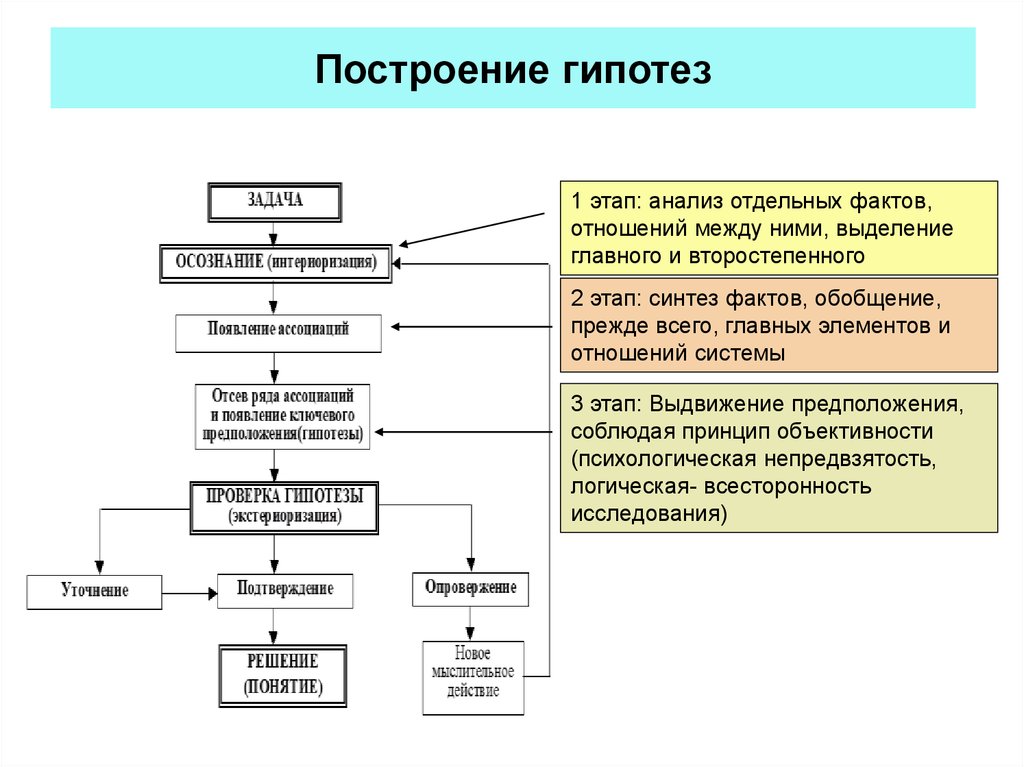
7. С целью формирования представлений о десятке как новой счетной единице
проводятся упражнения на:
1) счет однородных предметов группами по 2, 3, 4, 5, …, 10 элементов в каждой
группе;
2) измерение длин отрезков с помощью дециметра;
3) решение примеров вида а + b = 10;
4) осознание того, что результат счета зависит от единицы счета;
5) решение текстовых задач с ответом 10.
8. Установите логическую последовательность этапов изучения темы «Умножение многозначных чисел».
1) Умножение на круглые числа.
2) Умножение на однозначное число.
3) Умножение числа на произведение.
4) Умножение на двузначные и трехзначные числа.
5) Умножение числа на сумму.
9. Установите логическую последовательность изучения темы «Сложение и вычитание в пределах 10» по программе авторского коллектива под руководством
М.И. Моро.
1) Прибавление (вычитание) единицы.
2) Переместительное свойство сложения.
3) Прибавление (вычитание) 2, 3, 4 по частям.
4) Вычитание чисел 5, 6, 7, 8, 9.
5) Прибавление 5, 6, 7, 8, 9 (в сумме до 10). Таблица сложения.
6) Взаимосвязь сложения и вычитания.
10. Ориентировочной основой приема табличного вычитания с переходом через десяток являются:
1) состав числа 10;
2) присчитывание по одному;
3) состав однозначных чисел;
4) вычитание из чисел второго десятка всех отдельных единиц, т.е. вычитание типа
12 – 2;
5) правило вычитания суммы из числа.
11. На этапе постановки учебной задачи учитель предлагает ученикам разделить
круг на 8 равных частей и закрасить 3 части. Значит, тема этого урока:
1) деление с остатком; 2) дробь; 3) деление на равные части; 4) доли.
12. С целью создания затруднения при введении приема письменного деления на однозначное число целесообразно предложить ученикам выполнить (за ограниченный промежуток времени) деление в случаях:
1) 248 : 2; 2) 560 : 4; 3) 672 : 6; 4) 852 : 3; 5)
572 : 4; 6) 3600 : 2.
13. На этапе актуализации опорных знаний на уроке по теме «Табличное вычитание с переходом через десяток» используются задания на:
1) состав числа 10;
2) состав однозначных чисел;
3) отсчитывание по 1;
4) вычитание из чисел второго десятка всех отдельных единиц;
5) правило вычитания суммы из числа.
14. На этапе «Самостоятельная работа с самопроверкой» на уроке на тему «Умножение двузначного числа на однозначное» можно использовать задание «Найди значения выражений»:
1) 18 _ 4; 2) (32 + 18) _ 5; 3) 123 _ 7; 4) 23 _ 2; 5) 60 : 5 + 13 _ 6.
Ответы: Методика формирования у младших школьников вычислительной культуры
1. Ответ: 1, 2, 5.
2. Ответ: 3.
3. Ответ: 1, 2, 4, 6.
4. Ответ: 1, 2.
5. Ответ: 4, 1, 2, 3.
6. Ответ: 1, 2, 3, 5.
7. Ответ: 1, 4.
8.
Ответ: 2, 3, 1, 5, 4.
9. Ответ: 1, 3, 2, 5, 6, 4.
10. Ответ: 1, 3, 4.
11. Ответ: 2.
12. Ответ: 4, 5.
13. Ответ: 1, 2, 4.
14. Ответ: 1, 4.
III Методика обучения младших школьников решению текстовых задач
1. Ситуация, описанная на естественном языке, с требованием дать количественную
характеристику какого либо компонента данной ситуации — это ____________.
2. Основными компонентами текстовой задачи являются:
1) условие; 2) числовые данные; 3) графическая модель; 4) требование;
5) таблица.
3. Задача: «У Маши было 3 яблока, а у Саши на 2 яблока больше. Сколько яблок
было у Саши?» по классификации М.А. Бантовой является задачей на:
1) нахождение суммы;
2) увеличение числа на несколько единиц в прямой форме;
3) нахождение остатка;
4) разностное сравнение;
5)
нахождение целого.
4. Текстовая задача стандартной структуры — это задача, условие которой выражено повествовательным предложением, а требование выражено ___________ .
5. Задачи с величинами, характеризующими процессы движения, работы, купли продажи, называются задачами с _______ величинами.
6. Задача: «На первой полке книг на 5 больше, чем на второй, а на второй полке
книг на 3 больше, чем на третьей. На сколько книг на первой полке больше, чем на
третьей?» является:
1) составной; 2) сложной; 3) простой; 4) трудной; 5) занимательной.
7. К приемам анализа текста задачи относят:
1) установление отношений между данными и искомыми;
2) выделение условия и вопроса;
3) составление обратной задачи;
4) деление задачи на смысловые части;
5) словарную работу.
8. Найдите методы разбора текстовых задач (составления плана решения).
1) Аналитический.
2) Исчерпывающих проб.
3)
Алгоритмический.
4) Упорядоченный.
5) Индуктивный.
9. Найдите способы проверки решения задачи.
1) Составление и решение обратной задачи.
2) Установление соответствия между данными и искомыми.
3) Решение задач, различных по сюжету, но сходных по математической структуре.
4) Решение задачи другим методом.
5) Пересчет.
10. Подготовительная работа к введению простых задач заключается в:
1) формировании представлений о смысле действий сложения и вычитания;
2) составлении математических рассказов по иллюстрации и серии иллюстраций;
3) обучении счету предметов группами;
4) обучении предметному и схематическому моделированию;
5) развитии мыслительных операций.
11. Задача, ответ на вопрос которой может быть получен только посредством
рассуждений и умозаключений, называется _________ .
12. Приемы выделения компонентов текстовой задачи, переформулировки текста задачи и деления текстовой задачи на смысловые части уместно использовать на этапе:
1) поиска решения задачи;
2) решения задачи;
3) анализа содержания задачи;
4)
дополнительной работы над задачей.
13. Установите последовательность этапов работы над задачей.
1) Дополнительная работа над решенной задачей.
2) Поиск решения задачи.
3) Анализ и усвоение текста задачи.
4) Проверка решения задачи.
5) Решение задачи.
14. В ходы обучения младших школьников решению задач разными способами целесообразно использовать приемы:
1) переформулировки условия задачи;
2) восстановления решения по первому действию;
3) пояснения готового решения;
4) разбора задачи методом «исчерпывающих проб»;
5) составления и решения обратной задачи.
15.Содержание подготовительной работы к введению составных задач заключается в:
1) знакомстве со смыслом действий сложения и вычитания;
2) обучении младших школьников схематическому моделированию;
3) решении простых задач цепочек;
4) упражнениях на подбор различных вопросов к одному условию;
5) решении задач с недостающими данными.
Ответы: Методика обучения младших школьников решению текстовых задач
1.
Ответ: текстовая задача.
2. Ответ: 1, 4.
3. Ответ: 2.
4. Ответ: вопросом, вопросительным предложением.
5. Ответ: пропорциональными.
6. Ответ: 3.
7. Ответ: 1, 2, 4, 5.
8. Ответ: 1, 2.
9. Ответ: 1, 2, 4, 5.
10. Ответ: 1, 2, 4, 5.
11. Ответ: логической.
12. Ответ: 3.
13. Ответ: 3, 2, 5, 4, 1.
14. Ответ: 2, 3, 4.
15. Ответ: 2, 3, 4, 5.
IV Методика изучения пропедевтического материала в начальном математическом образовании.
1. Найдите утверждения, подтверждающие, что площадь — это величина.
1) Площадь можно измерить и выразить результат измерения числом.
2) Площадь имеют все фигуры, ограниченные замкнутой линией.
3) Площадь — это место в городе.
4)
Площадь характеризует свойство предмета занимать место на плоскости (поверхности).
2. Отметьте верные высказывания.
1) Килограмм, литр и метр — это единицы массы, объема и длины.
2) 1 000 000 000 000 мм = 1 000 000 км.
3) Площадь круга больше площади квадрата, построенного на диаметре круга.
4) Объем — это величина, характеризующая размер любых геометрических фигур.
3. Отметьте неверные высказывания.
1) Точка, линия, отрезок — это фигуры нулевой площади.
2) Масса двух одинаковых по размеру коробок всегда одинакова.
3) Углы сравнивают по величине наложением.
4) Сравнивая предметы по массе с помощью мускульных усилий, легко ошибиться.
5) Чем больше мерка, тем больше число, полученное в результате измерения величины.
4. Дидактические цели изучения темы «Меры времени» в начальной школе формулируются так:
1) воспитание бережного отношения к природе;
2) расширение кругозора учащихся за счет изучения исторического материала;
3) формирование представления о времени как о величине, характеризующей
длительность и хронологию событий;
4) углубление пространственно временных представлений младших школьников;
5)
знакомство с временами года и их признаками.
5. Отметьте неверные высказывания.
1) 1 км/мин = 60 км/ч.
2) Все геометрические фигуры имеют площадь.
3) Все плоские геометрические фигуры имеют нулевой объем.
4) Углы можно сравнить по величине только при помощи измерения их градусной меры транспортиром.
5) При измерении длины отрезка разными мерками получится одно и то же численное значение величины.
6. Установите последовательность изучения градусной меры угла.
1) Сравнение углов непосредственно (визуально, наложением).
2) Опосредованное сравнение углов с использованием различных мерок.
3) Формирование представлений об угле, видах углов.
4) Введение градуса как единой единицы измерения величины угла.
5) Тренировка в измерении величины угла и построении углов заданной градусной меры.
7. Учащиеся выполняют измерение величин с помощью различных мерок с
целью:
1) осознания зависимости между меркой и числом, полученным в результате измерения;
2) развития практических умений и навыков;
3) формирования умений работать в группах;
4) осознанного выбора единой (общепринятой) единицы измерения конкретной
величины.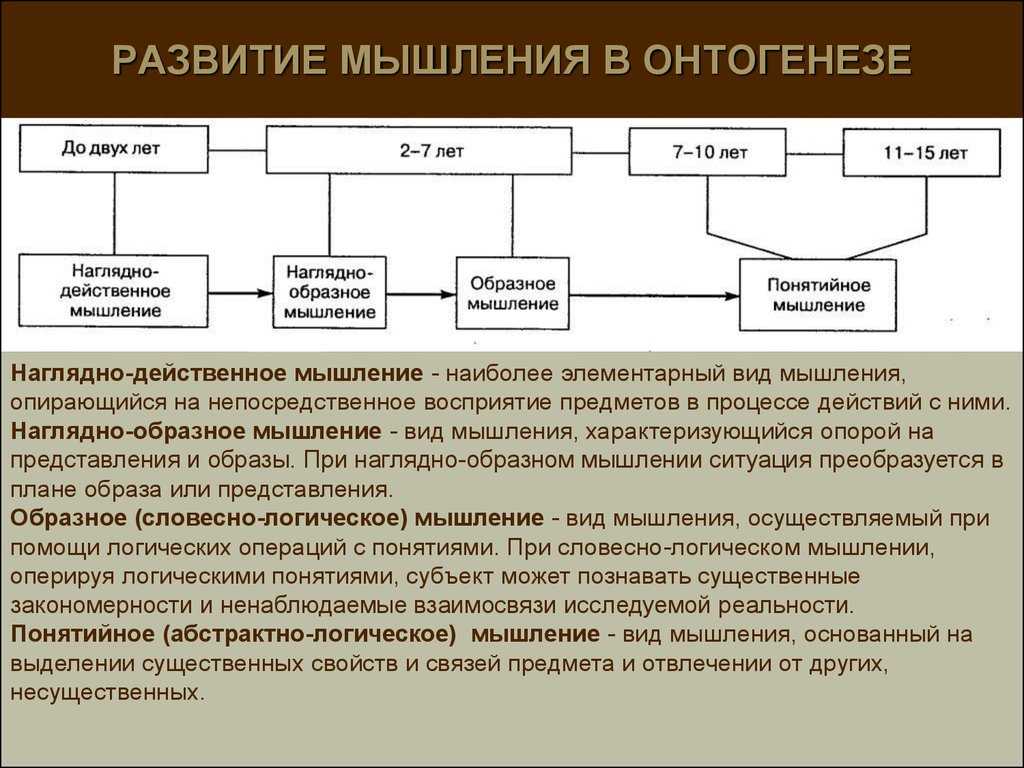
8. Установите соответствие между названием этапа и его содержанием.
1) Опосредованное сравнение величин; 2) введение стандартных единиц измерения величин; 3) свойства величин; 4) непосредственное сравнение величин.
а) Сравнение величин визуально, с помощью мускульных усилий, наложением;
б) сравнение, сложение, вычитание однородных величин, умножение и деление
величин на число, нахождение кратного отношения величин;
в) измерение величин различными мерками, исследование взаимосвязи между
единицей величины и ее численным значением;
г) знакомство с см, л, кг, см2;
д) знакомство с измерительными инструментами (линейкой, палеткой, транспортиром, весами).
9. Представления о старинных единицах измерения величин (сажень, ярд и др.)
формируются с целью:
1) воспитания аккуратности;
2) формирования навыков работы с чертежными инструментами;
3) воспитания интереса к математике;
4) расширения кругозора;
5) обоснования необходимости введения стандартных (общепринятых) единиц
измерения величин;
6)
иллюстрации прикладной направленности математики.
10. Отметьте верные утверждения.
1) Учащиеся начальных классов смешивают понятия объем и масса.
2) Особую сложность для младших школьников представляет выполнение
действий с единицами времени.
3) Самая легкая для восприятия учащихся величина — это скорость.
4) Выпускник начальной школы может научиться измерять длину предметов, массу
тел, время (по часам), даты (по календарю), вместительность сосудов и площадь фигур.
5) В программе авторского коллектива под руководством М.И. Моро учащиеся
знакомятся с такими величинами, как температура и градусная мера угла.
11. На этапе постановки учебной задачи учитель предлагает учащимся II класса сосчитать количество прямых, острых и тупых углов, изображенных на карточке. Учащиеся выполнили задание по-разному. Значит, тема данного урока:
1) виды углов; 2) определение вида угла путем сравнения с прямым углом;
3)
построение углов; 4) сравнение углов методом наложения; 5) угол.
12. Установите последовательность учебных ситуаций для этапа актуализации
знаний урока по теме «Сантиметр».
1) Визуальное сравнение длин предметов (лент, полосок бумаги).
2) Задание на классификацию по различным признакам (цвету, форме, длине).
3) Сравнение предметов, близких по длине, методом наложения.
4) Сравнение длин предметов с использованием различных мерок.
13. Найдите упражнения, предупреждающие смешение понятий круг и окружность.
1) Отметь точки, лежащие внутри круга, вне круга, на окружности.
2) Сравни многоугольник и круг.
3) Измерь длину окружности и площадь круга, используя нитку и палетку.
4) Проведи окружность и раскрась круг.
5) Выдели цветом границу круга.
6) Начерти квадрат, сторона которого равна диаметру круга.
14. Найдите у упражнения на пропедевтику понятий равновеликость и равносоставленность геометрических фигур.
1) Игра «Танграмм».
2)
Вычисли площадь прямоугольника, если а = 3
см, b = 5 см.
3) Начерти все возможные фигуры площадью 12 см2.
4) Из квадрата, площадь которого 16 см2, составь прямоугольник, длина которого
равна 8 см. Чему равна площадь прямоугольника?
5) Что больше: площадь круга или площадь квадрата, построенного на его диаметре?
15. На этапе постановки учебной задачи учитель предлагает школьникам построить
четырехугольник с тремя прямыми углами. Значит, тема данного урока:
1) прямой угол; 2) виды углов; 3) прямоугольник; 4) площадь прямоугольника.
16. На этапе постановки учебной задачи учитель предлагает учащимся построить
прямоугольник с длинами сторон 2 см, 3 см, 4 см, 6 см. Значит, основная дидактическая цель данного урока:
1) сформировать представление о площади прямоугольника;
2) вывести формулу площади прямоугольника;
3) предупредить смешение понятий квадрат и прямоугольник;
4) сформировать представление о равенстве противоположных сторон прямоугольника.
17.
Функциональная
пропедевтика в начальном математическом образовании связана
с:
1) заполнением и исследованием таблиц;
2) изучением координатного угла;
3) исследованием решения задач с буквенными данными;
4) измерением величин различными мерками;
5) решением задач на нахождение суммы и остатка.
18. В ходе подготовки к введению понятия уравнение ученики выполняют задания на:
1) составление и анализ таблицы сложения;
2) заполнение пропусков в равенствах вида _ + 3 = 7;
3) сравнение единиц площади;
4) выполнение вычислений с помощью числового отрезка;
5) дифференциацию равенств, неравенств и математических выражений.
19. При введении понятия уравнение учитель обращает внимание младших
школьников на то, что уравнение — это равенство:
1) содержащее неизвестное число, которое может быть обозначено любым символом;
2) с окошком;
3) двух функций;
4) содержащее неизвестный компонент арифметического действия, который обозначен буквой латинского алфавита;
5)
предикат, в записи которого используется знак равенства.
20. Для осознания учащимися смысла термина уравнение нужно использовать:
1) ассоциативный способ решения уравнений;
2) дидактические игры;
3) метод подбора корня уравнения;
4) методику «Весы»;
5) алгебраический метод решения задач.
21. Найдите задания из курса математики начальной школы на иллюстрацию
свойств прямой и обратной пропорциональной зависимости.
1) Измерение величин различными мерками.
2) Исследование зависимости между компонентами и результатами арифметических действий умножения и деления.
3) Сравнение и дифференциация математических объектов (выражений, задач,
геометрических фигур).
4) Исследование зависимости между компонентами и результатами действий
сложения и вычитания.
5) Решение задач с величинами, характеризующими какие-либо процессы.
22. При выполнении этих заданий у учащихся формируется способность к символьной записи.
1) Игра «Танграмм».
2)
Графический диктант.
3) Запись высказываний на математическом языке.
4) Фиксация нового знания в знаковой форме (опорный конспект).
5) Запись законов и свойств арифметических действий в общем виде.
23. На этапе постановки учебной задачи учитель предлагает учащимся записать одним выражением группу примеров (250 : 10, 250 : 25, 250 : 50, 250 : 5). Значит, тема данного урока:
1) выражение; 2) равенство; 3) уравнение; 4) переменная; 5) деление многозначных чисел.
24. На этапе постановки учебной задачи учитель предлагает учащимся записать на
языке математики высказывание «Масса арбуза меньше 5 кг, но больше 3 кг». Значит, тема данного урока:
1) двойное неравенство; 2) неравенство; 3) равенство; 4) нестрогое неравенство;
5) неравенство с двумя условиями.
Ответы: Методика изучения пропедевтического материала в начальном математическом образовании.
1. Ответ: 1, 4.
2. Ответ: 1, 2.
3.
Ответ: 2,
5.
4. Ответ: 2, 3, 4.
5. Ответ: 2, 4, 5.
6. Ответ: 3, 1, 2, 4, 5.
7. Ответ: 1, 4.
8. Ответ: 1в, 2г, 3б, 4а.
9. Ответ: 3, 4, 5, 6.
10. Ответ: 1, 2, 4.
11. Ответ: 2.
12. Ответ: 2, 1, 3, 4.
13. Ответ: 1, 3, 4, 5.
14. Ответ: 1, 3, 4.
15. Ответ: 3.
16. Ответ: 4.
17. Ответ: 1, 2, 3, 4.
18. Ответ: 2, 5.
19. Ответ: 4.
20. Ответ: 3, 4.
21. Ответ: 1, 2, 5.
22. Ответ: 3, 4, 5.
23. Ответ: 4.
24. Ответ: 1.
Транстеоретическая модель (стадии изменений)
Транстеоретическая модель (также называемая моделью стадий изменений), разработанная Прочаской и ДиКлементе в конце 1970-х гг. требующие дальнейшего лечения, чтобы понять, почему некоторые люди были способны бросить курить самостоятельно.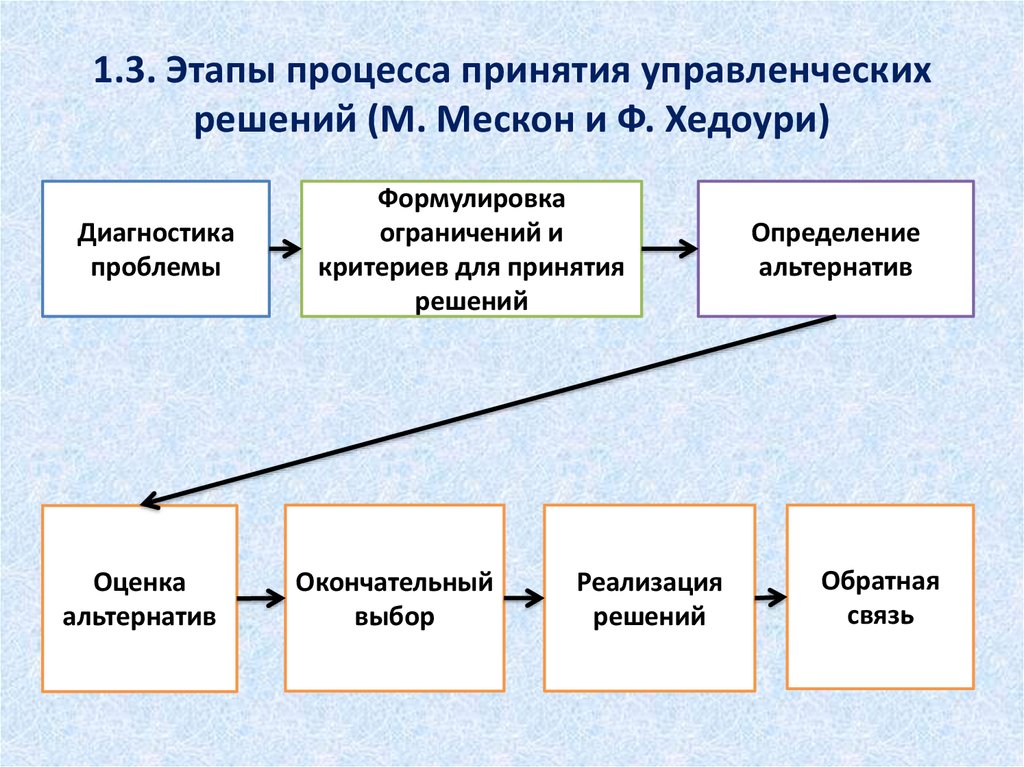
Было установлено, что люди бросают курить, если они к этому готовы. Таким образом, Транстеоретическая модель (ТТМ) фокусируется на принятии решений человеком и представляет собой модель преднамеренных изменений. ТТМ исходит из того, что люди не меняют свое поведение быстро и решительно. Скорее, изменение поведения, особенно привычного поведения, происходит непрерывно посредством циклического процесса. ТТМ — это не теория, а модель; различные поведенческие теории и конструкции могут применяться на различных этапах модели, где они могут быть наиболее эффективными.
ТТМ утверждает, что люди проходят шесть стадий изменения: предварительное обдумывание, обдумывание, подготовка, действие, поддержание и прекращение. Прекращение не было частью исходной модели и реже использовалось при применении стадий изменения поведения, связанного со здоровьем. Для каждого этапа изменений различные стратегии вмешательства наиболее эффективны для перехода человека к следующему этапу изменений, а затем через модель к поддержанию идеального поведения.
- Предварительное обдумывание. На этом этапе люди не намерены предпринимать никаких действий в обозримом будущем (определяется как ближайшие 6 месяцев). Люди часто не осознают, что их поведение проблематично или приводит к негативным последствиям. Люди на этой стадии часто недооценивают плюсы изменения поведения и слишком много внимания уделяют минусам изменения поведения.
- Созерцание. На этом этапе люди намерены начать вести здоровый образ жизни в обозримом будущем (определяется как ближайшие 6 месяцев). Люди осознают, что их поведение может быть проблематичным, и имеют место более вдумчивое и практическое рассмотрение плюсов и минусов изменения поведения с одинаковым акцентом на обоих. Даже при таком признании люди могут по-прежнему испытывать двойственное отношение к изменению своего поведения.
- Подготовка (решительность) — на этом этапе люди готовы действовать в течение следующих 30 дней. Люди начинают делать небольшие шаги к изменению поведения и верят, что изменение своего поведения может привести к более здоровой жизни.
- Действие. На этом этапе люди недавно изменили свое поведение (определяемое как последние 6 месяцев) и намерены продолжать двигаться вперед с этим изменением поведения. Люди могут проявлять это, изменяя свое проблемное поведение или приобретая новое здоровое поведение.
- Поддержание. На этом этапе люди сохраняют изменение своего поведения в течение некоторого времени (определяемого как более 6 месяцев) и намерены поддерживать изменение поведения в будущем. Люди на этой стадии работают над предотвращением возврата к более ранним стадиям.
- Прекращение — на этой стадии люди не хотят возвращаться к своему нездоровому поведению и уверены, что они не вернутся. Так как это редко достигается, и люди, как правило, остаются на стадии поддержания, эта стадия часто не учитывается в программах укрепления здоровья.
Для прохождения этапов изменений люди применяют когнитивные, аффективные и оценочные процессы. Было определено десять процессов изменений, причем некоторые процессы более актуальны для определенного этапа изменений, чем другие процессы.
Эти процессы приводят к стратегиям, которые помогают людям вносить и поддерживать изменения.
- Повышение сознания — Повышение осведомленности о здоровом поведении.
- Драматическое облегчение — Эмоциональное возбуждение по поводу поведения в отношении здоровья, будь то положительное или отрицательное возбуждение.
- Самооценка. Самооценка для осознания того, что здоровое поведение является частью того, кем они хотят быть.
- Экологическая переоценка — социальная переоценка, чтобы понять, как их нездоровое поведение влияет на других.
- Социальное освобождение — Экологические возможности, которые существуют, чтобы показать, что общество поддерживает здоровое поведение.
- Самоосвобождение — Обязательство изменить поведение, основанное на вере в то, что достижение здорового поведения возможно.
- Помогающие отношения — Поиск поддерживающих отношений, которые способствуют желаемым изменениям.
- Контробусловливание — замена нездорового поведения и мыслей здоровым поведением и мыслями.
- Управление подкреплением — Вознаграждение за положительное поведение и уменьшение вознаграждения за негативное поведение.
- Stimulus Control — Реинжиниринг окружающей среды, чтобы иметь напоминания и сигналы, которые поддерживают и поощряют здоровое поведение, и удаляют те, которые поощряют нездоровое поведение.
Существует несколько ограничений ТТМ, которые следует учитывать при использовании этой теории в общественном здравоохранении. Ограничения модели включают следующее:
- Теория игнорирует социальный контекст, в котором происходят изменения, такие как СЭС и доход.
- Линии между стадиями могут быть произвольными без установленных критериев того, как определить стадию изменения человека. Анкеты, разработанные для определения человека на стадии изменения, не всегда стандартизированы или утверждены.
- Нет четкого представления о том, сколько времени требуется для каждой стадии или как долго человек может оставаться на стадии.
- Модель предполагает, что люди строят последовательные и логичные планы в процессе принятия решений, хотя это не всегда верно.
Транстеоретическая модель предлагает стратегии вмешательств в области общественного здравоохранения, направленные на людей на различных этапах процесса принятия решений. Это может привести к тому, что вмешательства будут адаптированы (т. е. сообщение или компонент программы будут специально созданы для уровня знаний и мотивации целевой группы населения) и эффективны. TTM поощряет оценку текущего этапа изменений человека и учитывает рецидивы в процессе принятия решений людьми.
вернуться наверх | предыдущая страница | следующая страница
Психомоторный домен
Психомоторный доменТаксономия психомоторной области
Эта область характеризуется прогрессивными уровнями поведения от наблюдения к овладению физическим навыком. Несколько разных существуют таксономии.
Симпсон (1972) построил эту таксономию на основе работы Блума и других:
- Восприятие — Сенсорные сигналы определяют двигательную активность.Набор
- — Умственные, физические и эмоциональные предрасположенности, которые делают человека реагировать определенным образом на ситуацию.
- Управляемый ответ — Первые попытки физического навыка. Суд и ошибки в сочетании с практикой приводят к лучшей производительности.
- Механизм — промежуточный этап в изучении физического навыка. Ответы привычны со средним уровнем уверенности и профессионализма.
- Комплексная явная реакция — сложные движения возможны с минимум ненужных усилий и высокий уровень уверенности в том, что они будут успешный.
- Адаптация — Движения могут быть изменены для особых ситуаций.
- Происхождение — новые движения могут быть созданы для особых ситуаций.
Симпсон, Э. (1972). Классификация образовательных цели в психомоторном домен: психомоторный домен. Том. 3. Вашингтон, округ Колумбия: Грифон Дом.
Дэйв (1970) разработал эту таксономию:
- Подражание — Наблюдение и копирование кого-то другого.
- Манипуляция — Руководствуйтесь инструкциями по выполнению навыка.
- Точность — в навыке присутствуют точность, пропорция и аккуратность. исполнение без наличия первоисточника.
- Артикуляция — два или более навыка в сочетании, последовательности и выполняются последовательно.
- Натурализация — Сочетание двух или более навыков, последовательных и выполняется последовательно и легко. Производительность автоматическая с небольшая физическая или умственная нагрузка.
На основании R. H. Dave, как сообщается в R. J. Armstrong et al., Разработка и написание поведенческих задач (Тусон, Аризона: Пресса для новаторов в области образования, 1970).
Harrow (1972) разработал эту таксономию. Он организован в соответствии с степень координации, включая непроизвольные реакции и усвоенные возможности:
- Рефлекторные движения. Автоматические реакции.
- Базовое фундаментальное движение — Простые движения, которые можно дополнить
более сложные комплексы движений.
- Восприятие — сигналы окружающей среды, которые позволяют приспособиться движения.
- Физические нагрузки. Вещи, требующие выносливости, силы, энергичность, ловкость.
- Умелые движения. Деятельность, где уровень эффективности достигнуто.
- Недискурсивное общение — Язык тела.
Харроу, А.Дж. (1972). Таксономия психомоторной области. Нью-Йорк: Дэвид Маккей Ко.
Следующий список представляет собой комбинацию вышеуказанных таксономий:
| Психомоторный Домен | ||
| Уровень | Определение | Пример |
| 1. Наблюдение | Активное мысленное сопровождение физического события.
| Ученик наблюдает за более опытным человек. Другая умственная деятельность, такая как чтение, может быть частью процесс наблюдения. |
| 2. Подражание | Попытка копирования физического поведения. | Первые шаги в изучении навыка. Ученик наблюдается и получает указания и отзывы о производительности. Движение не является автоматическим или плавным. |
| 3. Практика | Многократные попытки заниматься определенной физической деятельностью. | Навык повторяется снова и снова. Вся последовательность выполняется неоднократно. Движение движется к тому, чтобы стать автоматическим и гладкий. |
| 4. Адаптация | Тонкая настройка. Вносим небольшие коррективы в
физическую активность для ее совершенствования. About the Author Related Posts | |