Дедуктивная логика это: Логика дедуктивная – Гуманитарный портал

Логика дедуктивная – Гуманитарный портал

Дедуктивная логика — это раздел логики (см. Логика), в котором изучаются дедуктивные рассуждения (см. Дедукция), то есть рассуждения, гарантирующие истинность заключения при истинности его посылок. Дедуктивная логика иногда отождествляется с формальной логикой (см. Логика формальная). Вне пределов дедуктивной логики находятся так называемые правдоподобные рассуждения (см. Рассуждения правдоподобные) и индуктивные методы (см. Индукция), которые изучаются в индуктивной логике (см. Логика индуктивная). В дедуктивной логике исследуются способы рассуждений со стандартными, типовыми высказываниями; эти способы оформляются в виде логических систем, или исчислений. Исторически первой системой дедуктивной логики была силлогистика Аристотеля (см. Силлогистика). В свою очередь стоики первыми предприняли попытки построения дедуктивной логики в виде логики высказываний (см.  Логика высказываний). Г. Фреге и Ч. С. Пирс расширили область этой логики — в качестве типовых высказываний стали рассматриваться высказывания об отношениях и были введены кванторы. Наиболее важной системой дедуктивной логики является классическая логика предикатов первого порядка (см. Логика предикатов). В рамках этой системы отношение логического следования (см. Логическое следование), может быть полностью формализовано, и способы рассуждений могут быть описаны чисто синтаксически. Были построены также второпорядковая логика предикатов и системы более высоких порядков. Однако, согласно теореме К. Гёделя, отношение логического следования вторпорядковой логики предикатов в принципе неформализуемо. В настоящее время интенсивно изучаются системы дедуктивной логики, лежащие между первопорядковой и второпорядковой логиками, системы с обобщёнными кванторами, с эпсилон-символом и другими, а также системы с нефинитными правилами (типа правила бесконечной индукции). Стремление учесть в рассуждениях специфику познаваемых объектов, фактор роста и накопления знания, неопределённость понятия истинности высказываний, возможность мыслить противоречивые объекты и ситуации привели к построению различных систем так называемых [дедуктивных] неклассических логик (см.  Логики неклассические), интуиционистской, модальной, многозначной, релевантной, паранепротиворечивой и других. Стали исследоваться логические системы с истинностными провалами и пресыщенными истинностными оценками. При этом широкое применение находят различные семантические методы, например, теория моделей, семантика возможных миров, операционная семантика и другие, а также разнообразные синтаксические методы: аксиоматические исчисления, натуральный вывод, исчисления секвенций , аналитические таблицы и другие. В ряде неклассических систем дедуктивной логики учитываются и прагматические аспекты рассуждений. В дедуктивной логике исследуются способы не только рассуждений, но и введения понятий (например, процедуры определения), а также методы к процедуры поиска доказательств. В последнее время на базе неклассической дедуктивной логики интенсивно развиваются так называемые динамические логики и логики программирования, ориентированные на проблемы компьютерных наук. Кроме того, разрабатываются логики действий, норм, императивов и предпочтений, ориентированные не только на проблемы искусственного интеллекта, но и на применение в области этики и права. Дедуктивная логика едина, а многообразие её систем определяется тем, что по частям исследуются способы рассуждений (см. Рассуждение), основанные на различных типах высказываний и применяемые в различных контекстах. В разных системах применяются различные формализованные языки, принимаются более или менее сильные абстракции и идеализации, учитываются или не учитываются различные характеристики знания. В дедуктивной логике исследуются также её взаимоотношения с различными другими (недедуктивными) логическими системами и даётся их семантико-эпистемологическое обоснование.

Байесовские методы в эконометрии

Байесовские методы в эконометрии

Зельнер А. Байесовские методы в эконометрии / Пер. с англ. Г. Г. Пирогова и Ю. П. Федоровского; с предисл. переводчиков. — М.: Статистика, 1980. — 438 с. В книге подробно рассмотрено применение теоремы Байеса об условной вероятности некоторого события при заданной вероятности другого события для решения проблем, связанных со статистическим оцениванием параметров экономических моделей. Этот подход дает возможность получить приемлемые с практической точки зрения оценки в условиях малых выборок. Для тех, кто занимается экономико-математическими исследованиями, вопросами сбора и обработки информации для экономических моделей; полезна также студентам и аспирантам. Оглавление ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ Глава 1. ЗАМЕЧАНИЯ О ВЫВОДЕ В ЭКОНОМИЧЕСКОЙ НАУКЕ 1.2. ДЕДУКТИВНЫЙ ВЫВОД 1.3. ИНДУКТИВНЫЙ ВЫВОД 1.4. РЕДУКТИВНЫЙ ВЫВОД 1.5. ПРАВИЛА ДЖЕФФРИСА ДЛЯ ТЕОРИИ ИНДУКТИВНОГО ВЫВОДА [66, с. 8]. 1.6. СЛЕДСТВИЯ, ВЫТЕКАЮЩИЕ ИЗ ПРАВИЛ ДЖЕФФРИСА ВОПРОСЫ И УПРАЖНЕНИЯ Глава 2. ПРИНЦИПЫ БАЙЕСОВСКОГО АНАЛИЗА С КОНКРЕТНЫМИ ПРИМЕРАМИ ПРИЛОЖЕНИЙ 2.2. ТЕОРЕМА БАЙЕСА И НЕСКОЛЬКО МАССИВОВ ДАННЫХ 2.3. АПРИОРНЫЕ ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 2.4. МАРГИНАЛЬНЫЕ И УСЛОВНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ 2.5. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ 2.6. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ И ОБЛАСТИ ДЛЯ ПАРАМЕТРОВ 2.7. МАРГИНАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ НАБЛЮДЕНИЙ 2.8. ПРОГНОЗНЫЕ ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 2.9. ТОЧЕЧНЫЙ ПРОГНОЗ 2.10. ПРОГНОЗНЫЕ ОБЛАСТИ И ИНТЕРВАЛЫ 2.11. НЕКОТОРЫЕ СВОЙСТВА БАЙЕСОВСКИХ АПОСТЕРИОРНЫХ ФПВ ПРИ БОЛЬШИХ ВЫБОРКАХ 2.12. ПРИЛОЖЕНИЕ ВЫШЕИЗЛОЖЕННЫХ ПРИНЦИПОВ К АНАЛИЗУ РАСПРЕДЕЛЕНИЯ ПАРЕТО 2.13. ПРИЛОЖЕНИЕ ВЫШЕИЗЛОЖЕННЫХ ПРИНЦИПОВ К АНАЛИЗУ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ 2.14. ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ БАЙЕСОВСКОГО АНАЛИЗА ПРИЛОЖЕНИЕ. АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ, ПРЕДСТАВЛЯЮЩИЕ «СКУДОСТЬ ЗНАНИЯ» ВОПРОСЫ И УПРАЖНЕНИЯ Глава 3. ОДНОМЕРНАЯ НОРМАЛЬНАЯ ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ 3.1.2. Апостериорные ФПВ для параметров с расплывчатой априорной ФПВ 3.1.3. Приложение результатов для анализа мультипликатора инвестиций 3.2. НОРМАЛЬНАЯ МНОГОМЕРНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ 3.2.2. Апостериорные ФПВ для параметров в условиях расплывчатых априорных ФПВ 3.2.3. Апостериорная ФПВ, базирующаяся на информативных априорных ФПВ 3.2.4. Прогнозная ФПВ 3.2.5. Анализ моделей при условии вырожденности матрицы Х’Х ВОПРОСЫ И УПРАЖНЕНИЯ ГЛАВА 4. СПЕЦИАЛЬНЫЕ ПРОБЛЕМЫ РЕГРЕССИОННОГО АНАЛИЗА 4.2. СЛУЧАЙ РЕГРЕССИИ С НЕОДИНАКОВЫМИ ДИСПЕРСИЯМИ 4.3. ДВЕ РЕГРЕССИИ, НЕКОТОРЫЕ ИЗ КОЭФФИЦИЕНТОВ КОТОРЫХ СОВПАДАЮТ ПРИЛОЖЕНИЕ 1 ПРИЛОЖЕНИЕ 2 ВОПРОСЫ И УПРАЖНЕНИЯ Глава 5. ОШИБКИ В ПЕРЕМЕННЫХ 5.1. КЛАССИЧЕСКАЯ МОП: ПРЕДВАРИТЕЛЬНЫЕ ЗАДАЧИ 5.2. КЛАССИЧЕСКАЯ МОП: АНАЛИЗ ФУНКЦИОНАЛЬНОЙ ФОРМЫ МЕТОДОМ НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ 5.3. АНАЛИЗ СТРУКТУРНОЙ ФОРМЫ МОП МЕТОДОМ НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ 5. 4. БАЙЕСОВСКИЙ АНАЛИЗ ФУНКЦИОНАЛЬНОЙ ФОРМЫ МОП 5.5. БАЙЕСОВСКИЙ ДИАЛИЗ СТРУКТУРНОЙ ФОРМЫ МОП 5.6. АЛЬТЕРНАТИВНЫЕ ДОПУЩЕНИЯ О ВЕТВЯЩИХСЯ ПАРАМЕТРАХ ПРИЛОЖЕНИЕ ВОПРОСЫ И УПРАЖНЕНИЯ Глава 6. АНАЛИЗ НЕЛИНЕЙНЫХ МОДЕЛЕЙ, СОСТОЯЩИХ ИЗ ОДНОГО УРАВНЕНИЯ 6.2. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ ПОСТОЯННОЙ ЭЛАСТИЧНОСТИ ЗАМЕНЫ (ПЭЗ) 6.3. ОБОБЩЕННЫЕ ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ ВОПРОСЫ И УПРАЖНЕНИЯ Глава 7. МОДЕЛИ ВРЕМЕННЫХ РЯДОВ: НЕСКОЛЬКО ИЗБРАННЫХ ПРИМЕРОВ 7.2. МОДЕЛЬ АВТОРЕГРЕССИОННОГО ПРОЦЕССА ПЕРВОГО ПОРЯДКА, ОСНОВАННАЯ НА НЕПОЛНЫХ ДАННЫХ 7.3. АНАЛИЗ АВТОРЕГРЕССИОННОГО ПРОЦЕССА ВТОРОГО ПОРЯДКА 7.4. МОДЕЛИ «РАСПРЕДЕЛЕННЫХ ЗАПАЗДЫВАНИЙ» (ЛАГОВ) 7.5. ПРИЛОЖЕНИЕ В ОБЛАСТИ ОЦЕНИВАНИЯ ФУНКЦИИ ПОТРЕБЛЕНИЯ 7.6. НЕКОТОРЫЕ ОБОБЩЕНИЯ МОДЕЛИ РАСПРЕДЕЛЕННОГО ЗАПАЗДЫВАНИЯ ПРИЛОЖЕНИЕ. РАСПЛЫВЧАТЫЕ АПРИОРНЫЕ ФПВ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ПРЕДСТАВЛЕНИЯ СТАЦИОНАРНЫХ АВТОРЕГРЕССИОННЫХ ПРОЦЕССОВ ВОПРОСЫ И УПРАЖНЕНИЯ Глава 8. МНОГОМЕРНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ 8.2. ПРОГНОЗНАЯ ФПВ ДЛЯ ТРАДИЦИОННОЙ МНОГОМЕРНОЙ РЕГРЕССИВНОЙ МОДЕЛИ 8. 3. ТРАДИЦИОННАЯ МНОГОМЕРНАЯ МОДЕЛЬ С ТОЧНЫМИ ОГРАНИЧЕНИЯМИ 8.4. ТРАДИЦИОННАЯ МОДЕЛЬ С ИНФОРМАТИВНОЙ АПРИОРНОЙ ФПВ 8.5. ПСЕВДОНЕЗАВИСИМАЯ РЕГРЕССИОННАЯ МОДЕЛЬ ВОПРОСЫ И УПРАЖНЕНИЯ Глава 9. ОДНОВРЕМЕННЫЕ УРАВНЕНИЯ В ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЯХ 9.1. ПОЛНОСТЬЮ РЕКУРСИВНЫЕ МОДЕЛИ 9.2. ОБЩИЕ ТРЕУГОЛЬНЫЕ СИСТЕМЫ 9.3. КОНЦЕПЦИЯ ИДЕНТИФИЦИРУЕМОСТИ В БАЙЕСОВСКОМ АНАЛИЗЕ 9.4. АНАЛИЗ НЕКОТОРЫХ КОНКРЕТНЫХ МОДЕЛЕЙ, ПРЕДСТАВЛЕННЫХ СИСТЕМАМИ ОДНОВРЕМЕННЫХ УРАВНЕНИИ 9.5. БАЙЕСОВСКИЙ АНАЛИЗ В УСЛОВИЯХ «ОГРАНИЧЕННОЙ ИНФОРМАЦИИ» 9.6. АНАЛИЗ ПОЛНОЙ СИСТЕМЫ 9.7. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ МОНТЕ-КАРЛО 9.7.2. Анализ модели методами теории выборочных исследований 9.7.3. Байесовский анализ модели 9.7.4. Экспериментальные результаты: точечные оценки 9.7.5. Экспериментальные результаты: доверительные интервалы 9.7.6. Заключительные замечания об экспериментах Монте-Карло ВОПРОСЫ И ЗАДАЧИ Глава 10. СРАВНЕНИЕ И ПРОВЕРКА ГИПОТЕЗ 10.1. АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ, СВЯЗАННЫЕ С ГИПОТЕЗАМИ 10. 2. АНАЛИЗ ГИПОТЕЗ С РАСПЛЫВЧАТЫМИ АПРИОРНЫМИ ФПВ ДЛЯ ПАРАМЕТРОВ 10.3. СРАВНЕНИЕ И ПРОВЕРКА ГИПОТЕЗ С НЕРАСПЛЫВЧАТОЙ АПРИОРНОЙ ИНФОРМАЦИЕЙ 10.4. СРАВНЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ 10.5. СРАВНЕНИЕ МОДЕЛЕЙ, РАСПРЕДЕЛЕННЫХ ЗАПАЗДЫВАНИЙ ВОПРОСЫ И УПРАЖНЕНИЯ Глава 11. АНАЛИЗ НЕКОТОРЫХ ЗАДАЧ УПРАВЛЕНИЯ 11.1. НЕКОТОРЫЕ ПРОСТЫЕ ОДНОПЕРИОДНЫЕ ЗАДАЧИ УПРАВЛЕНИЯ 11.2. ОДНОПЕРИОДНАЯ ЗАДАЧА УПРАВЛЕНИЯ ДЛЯ МНОЖЕСТВЕННЫХ РЕГРЕССИОННЫХ ПРОЦЕССОВ 11.3. УПРАВЛЕНИЕ В СЛУЧАЕ МНОГОМЕРНЫХ НОРМАЛЬНЫХ РЕГРЕССИОННЫХ ПРОЦЕССОВ 11.4. ЧУВСТВИТЕЛЬНОСТЬ УПРАВЛЕНИЯМ ЗАВИСИМОСТИ ОТ ВИДА ФУНКЦИИ ПОТЕРЬ 11.5. ДВУХПЕРИОДНАЯ ЗАДАЧА УПРАВЛЕНИЯ Б СЛУЧАЕ МНОЖЕСТВЕННОЙ РЕГРЕССИОННОЙ МОДЕЛИ 11.6. НЕКОТОРЫЕ МНОГОПЕРИОДНЫЕ ЗАДАЧИ УПРАВЛЕНИЯ ПРИЛОЖЕНИЕ 1. УСЛОВНАЯ ПРОГНОЗНАЯ ФПВ ДЛЯ z2 ПРИ ИЗВЕСТНОМ z1 ПРИЛОЖЕНИЕ 2. ВЫВОД ПРИБЛИЖЕННОГО МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ, ПРЕДСТАВЛЕННОГО В (11.72) ВОПРОСЫ И УПРАЖНЕНИЯ Глава 12. ЗАКЛЮЧЕНИЕ ПРИЛОЖЕНИЕ А. СВОЙСТВА НЕКОТОРЫХ ВАЖНЫХ ОДНОМЕРНЫХ ФПВ А. 2. ФПВ ОДНОМЕРНОГО t-РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА (О t-ФПВ С) Доказательство свойств О t-ФПВ А.3. ФПВ ГАММА- И «хи квадрат»-РАСПРЕДЕЛЕНИЙ (ГАММА-ФПВ И «хи квадрат»-ФПВ) А.4. ФПВ ОБРАТНОГО ГАММА-РАСПРЕДЕЛЕНИЯ (О ГАММА-ФПВ) А.5. ФПВ БЕТА-РАСПРЕДЕЛЕНИЯ (БЕТА-ФПВ) А.6. ФПВ РАСПРЕДЕЛЕНИЯ ФИШЕРА — СНЕДЕКОРА (Ф-ФПВ) ПРИЛОЖЕНИЕ Б. СВОЙСТВА НЕКОТОРЫХ МНОГОМЕРНЫХ ФПВ Б.2. МНОГОМЕРНАЯ ФПВ t-РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА (М t-ФПВ С) Б.3. ФПВ УИШАРТА (У-ФПВ) Б.4. ФПВ ОБРАТНОГО РАСПРЕДЕЛЕНИЯ УИШАРТА (О У-ФПВ) Б.5. ФПВ ОБОБЩЕННОГО -РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА (ОБ t-ФПВ С) БИБЛИОГРАФИЯ

Дедуктивная логика

Аргументы

Часто говорят, что академическое письмо — это вид письма, в котором приводится аргумент. По словам инструктора по письму Ленни Ирвина, «в колледже все споры» (2010, стр. 9). Что значит сказать, что академическое письмо является аргументом, или — это аргумент? Что такое аргумент?

Мы используем слово аргумент по крайней мере двумя разными способами. В каком-то смысле спор — это то, что делают два человека, когда они не согласны с чем-то. Если я скажу своему другу: «Пойди, принеси мне выпить», он может сказать мне: «Ни за что. Принеси сам». Это своего рода разногласие, но это не то, что мы имеем в виду, когда говорим, что академическое письмо является аргументом.

Аргумент , в том смысле, в каком мы его понимаем, представляет собой набор фактов, ведущих к заключению. Профессор когнитивистики Брэм ван Хевелн предлагает этот пример простого для понимания аргумента. Если вы хотите заказать пиццу и вам нужно решить, какую начинку заказать, вы можете подумать примерно так:

«Я не должен добавлять пепперони к своей пицце, потому что в последний раз, когда я добавлял пепперони в свою пиццу, я сильно заболел.» (Ван Хевелн, 2011)

Это аргумент. Он предлагает причину (, потому что в прошлый раз я сильно заболел, ), и эта причина поддерживает вывод (, я не должен есть пепперони в своей пицце, ).

Аргумент — это набор из одной или нескольких причин — в логике мы называем их предпосылками — которые поддерживают один вывод . В каждом хорошем аргументе посылки должны поддерживать вывод, и они должны быть верными. (Мы дадим определения этим терминам в разделе «Обоснованность и истина» ниже.) Это необходимые требования для всех хороших аргументов: причины должны быть связаны с выводом и, насколько нам известно, они должны быть истинными. Существует также третье качество, которому удовлетворяют многие хорошие аргументы: они учитывают всю информацию, относящуюся к заключению. Ван Хойвельн предлагает следующий пример аргумента, который не удовлетворяет третьему критерию:

По поводу пиццы отметим кое-что, что читатель, возможно, уже заметил сам: действительно ли из-за пепперони мне стало плохо в прошлый раз, или это просто совпадение? Может быть, я также выпил 6 стаканов колы, дюжину горячих крылышек и 2 пинты Ben and Jerry’s в тот судьбоносный день, когда я съел пиццу пепперони! В самом деле, если бы мы знали это, то, возможно, мы не были бы так впечатлены первоначальным аргументом о пицце. (Ван Хевелн, 2011)

Знание всей информации, относящейся к выводу, помогает нам судить о том, хорошо ли аргумент поддерживает вывод. Следовательно, многие хорошие аргументы включают в себя все соответствующие факты, и все хорошие аргументы должны включать верные предпосылки, связанные с выводом.

Дедуктивная логика против индуктивной

Система рассуждений с аргументами, предпосылками и выводами называется логикой . Существуют разные формальные системы логики — разные способы аргументации и разные способы письменного представления этих аргументов. Две основные системы называются индуктивная логика и дедуктивная логическая .

Индуктивная логика (или индуктивное рассуждение ) строит аргументы, поддерживающие вывод, но не претендует на то, чтобы показать, что вывод обязательно верен. Сильный индуктивный аргумент дает нам основания думать, что его вывод, скорее всего, верен. Некоторыми примерами индуктивных рассуждений являются обобщения, аналогии или статистические предсказания. Многие аргументы в естественных науках, социальных науках, гуманитарных науках и других академических областях направлены на то, чтобы показать, что конкретный вывод, вероятно, будет верным, и поэтому они основаны на индуктивной логике.

Дедуктивная логика (также называемая дедуктивным умозаключением или дедукцией ) является точной и хорошо упорядоченной системой, цель которой — обеспечить определенную поддержку для вывода. В то время как индуктивное рассуждение может показать, что вывод, вероятно, верен, дедуктивное рассуждение может показать, что вывод должен быть истинным. Другими словами, если мы используем дедуктивную логику и если у нас есть действительный аргумент с посылками, которые определенно верны, то мы можем гарантировать, что наш вывод верен. Некоторыми примерами дедуктивного рассуждения являются импликация и силлогизм.

Достоверность и истинность

Выше мы сказали, что если дедуктивный аргумент действителен и его посылки истинны , то его заключение должно быть истинным. Что мы подразумеваем под действительным и что мы подразумеваем под истинным ?

Достоверность – качество достоверности – относится к тому, как строится аргумент, а также к взаимосвязи между предпосылками и заключением. Помните, что посылки — это причины, которые поддерживают вывод. Аргумент действителен, если посылки «необходимо влекут за собой» вывод. Другими словами, исходя из того, как посылки сочетаются друг с другом, можно сделать только один вывод. Иными словами, «в некотором смысле «истина» вывода «содержится» в истине предпосылок» (Van Heuveln 2011). Это может быть трудно понять, поэтому давайте рассмотрим пример. Рассмотрим этот силлогизм:

Все лицензированные врачи Японии сдали экзамен Лицензионного совета.
Мои врачи имеют лицензию врача в Японии.
Поэтому мои врачи сдали экзамен в лицензионный совет.

Мы можем представить этот аргумент в виде картинки. На диаграмме ниже синий кружок представляет моих врачей. Желтый круг представляет всех лицензированных врачей в Японии. Зеленый кружок представляет людей, сдавших экзамен Лицензионного совета. Поскольку все люди, имеющие лицензию на практику врачей в Японии, прошли лицензионный совет, и поскольку все люди, которые являются моими врачами, входят в эту группу, то должно быть правдой, что все мои врачи прошли лицензионный совет. Экзамен. Синий круг обязательно находится внутри зеленого круга, поскольку весь синий круг находится внутри желтого круга, а весь желтый круг находится внутри зеленого круга. Именно это мы подразумеваем под «необходимым следствием».

Действительным аргументом является тот, вывод которого «содержится» в посылках или «неизбежно вытекает» из структуры аргумента. Другими словами, достоверность — это факт самого аргумента и отношения между посылками и заключением.

Истина, в отличие от достоверности, относится не только к самому аргументу. Посылки истинны, если они точно отражают реальный мир. В приведенном выше примере посылка «Мои врачи являются лицензированными врачами в Японии» верна, если есть несколько людей, которые являются моими врачами, и все они являются лицензированными врачами в Японии. Если это не так — например, если у меня есть врач, имеющий лицензию в другой стране, или если один из моих врачей практикует без лицензии — тогда посылка неверна.

Аргумент может быть действительным, даже если не все его предпосылки верны. Если один из моих врачей никогда не сдавал экзамен в лицензионный совет и практикует без лицензии, то вывод «Все мои врачи сдали экзамен в лицензионный совет» неверен. Аргумент по-прежнему действителен — синий кружок все еще находится внутри зеленого — но вывод оказывается верным только в том случае, если аргумент верен и посылки верны.

С другой стороны, истинность вывода не гарантирует правильности аргумента. Рассмотрим этот силлогизм:

Все люди — животные.
Некоторые животные живут в Японии.
Поэтому некоторые люди живут в Японии.

Каждая из предпосылок верна: все люди — животные, в том смысле, что они живые существа, которые едят и передвигаются. Также верно, что некоторые животные живут в Японии. Также верно и то, что некоторые люди живут в Японии. Но этот аргумент недействителен. Чтобы увидеть это, давайте попробуем представить его с помощью кругов, как мы делали раньше.

Мы знаем, что все люди — животные, но не все животные живут в Японии. Тот факт, что некоторые животные находятся в Японии, не обязательно означает, что некоторые люди находятся в Японии. В реальном мире мы знаем, что некоторые люди живут в Японии, но этот факт логически не следует из нашего аргумента. «Вывод» оказывается верным, но только случайно; аргумент недействителен.

Силлогизм

Одним из распространенных типов дедуктивных аргументов является силлогизм (иногда называемый стандартный , категорический , аристотелевский или дедуктивный силлогизм ).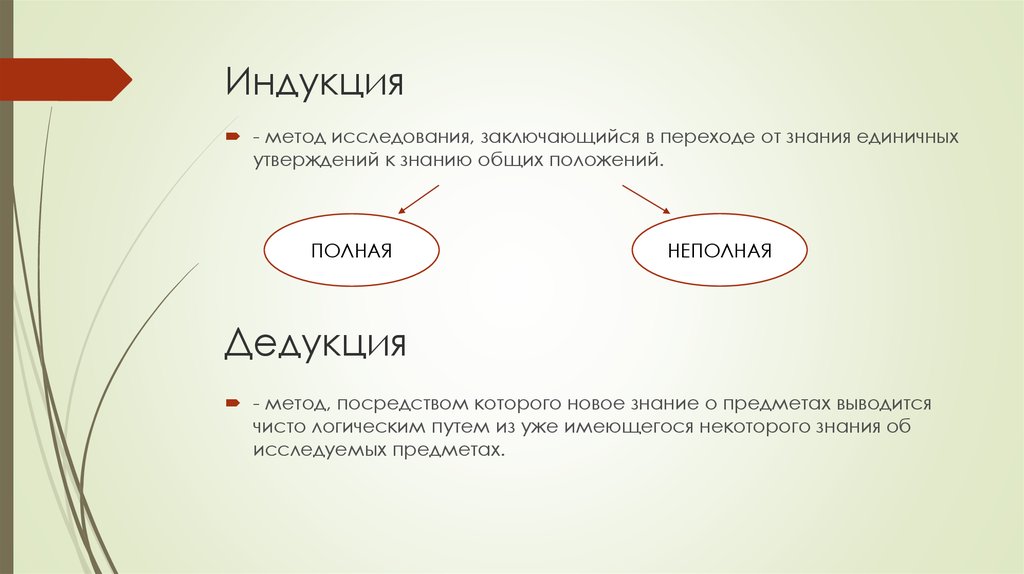 Силлогизм – это рассуждение, состоящее из двух посылок, которые поддерживают вывод. Эта форма силлогизма была разработана философом Аристотелем более двух тысяч лет назад и очень хорошо разработана и широко используется. (Намного больше истории и подробное описание см., например, в Smith 2017, Lagerlund 2016 или Parsons 2012.) Силлогизм этого типа состоит из набора категорических предложений , которые состоят из терминов . Мы определим категорические предложения и их термины в следующем разделе.

Категорические суждения

Типы утверждений, используемые в силлогизмах, подобных описанным здесь, называются «категорическими суждениями». Категориальные суждения содержат два «термина», подлежащее и сказуемое. (Значения «подлежащее» и «сказуемое» в логике немного отличаются от грамматических, но мы не будем здесь беспокоиться о конкретных различиях.) В следующем списке подлежащими являются подчеркнуто , а предикаты выделены курсивом .

• Аристотель философ .
• Немного философии это логика .
• Нет лошадей философы .
• Аристотель не лошадь .

Как мы уже говорили, все категориальные суждения имеют два термина: подлежащее и сказуемое. Кроме того, мы должны обратить внимание на количество и качество категорического предложения. Количество может быть как всеобщим (верным для всех или ничего), так и частным (верным для некоторых, что означает хотя бы одну вещь). Качество может быть как положительным ( равно ), так и отрицательным ( не , не ). Это приводит к четырем типам категорических предложений. В приведенной ниже таблице S означает подлежащее, а P означает сказуемое.

	Положительный	Отрицательный
Универсальный	Все S равно P например Все собаки млекопитающие.	Нет S есть P например Собаки не рыбы .
Частное	Некоторые S есть P например Некоторые млекопитающие являются плотоядными .	Некоторые S не являются P например Некоторые рыбы не являются хищниками .

 

Если мы хотим оценить логику части письма или речи, мы часто можем подумать о том, что это значит, и попытаться представить это как набор категориальных предложений. На приведенной ниже диаграмме показаны несколько категоричных утверждений, которые мы можем понять из обычного предложения о планктоне.

Планктон состоит из крошечных, часто одноклеточных растений, таких как диатомовые водоросли или водоросли, а также мелких или микроскопических животных, известных как зоопланктон.

Некоторый планктон является растениями. Часть планктона состоит из диатомовых водорослей. Некоторый планктон представляет собой водоросли Некоторый планктон является зоопланктоном. Весь планктон мелкий.

 

Мы можем использовать категорические утверждения для построения силлогизмов. Силлогизм — это тип рассуждения, в котором вывод делается из двух посылок. Посылки представляют собой категориальные утверждения, которые имеют один общий термин. Давайте еще раз посмотрим на приведенный выше пример силлогизма.

Все лицензированные врачи Японии сдали экзамен Лицензионного совета.
Мои врачи имеют лицензию врача в Японии.
Поэтому мои врачи сдали экзамен в лицензионный совет.

Каждая строка силлогизма представляет собой категорическое утверждение, состоящее из двух терминов. Обратите внимание, что один из терминов «лицензированные врачи в Японии» появляется в обоих посылках. Также каждый из терминов заключения (подлежащее «мои врачи» и сказуемое «сдал экзамен в лицензионной комиссии») появляется в одной из посылок. Это форма стандартного категорического силлогизма. Традиционно термин, который появляется в обеих посылках, называется «средним термином», подлежащее заключения называется «второстепенным термином», а сказуемое заключения — «большим термином». Но вам не нужно беспокоиться о запоминании этих ярлыков; полезно уметь распознавать действительный аргумент.

Давайте еще раз посмотрим на описание планктона и посмотрим, сможем ли мы найти логический аргумент.

Планктон состоит из крошечных, часто одноклеточных растений, таких как диатомовые водоросли или водоросли, а также мелких или микроскопических животных, известных как зоопланктон. Так как растения поглощают углекислый газ в процессе фотосинтеза, планктон может снижать уровень СО 2 в атмосфере. Хотя большая часть углерода в конечном итоге уходит обратно в атмосферу, часть опускается глубоко в океан в виде мертвых растений или зоопланктона.

Часть планктона — это растения. Все растения поглощают углекислый газ. Поэтому часть планктона поглощает углекислый газ.

 

Слово вместо в предложениях обычного языка предполагает, что текст приводит аргумент. Мы можем представить этот аргумент как силлогизм в нижнем ящике. Форма этого силлогизма верна. Если аргумент верен и посылки верны, мы знаем, что заключение должно быть верным. Следовательно, если верно, что некоторый планктон является растениями и все растения поглощают углекислый газ, то должно быть верно и то, что некоторый планктон поглощает углекислый газ. Можете ли вы привести другие аргументы этого типа?

Существуют сотни возможных форм аргументации, которые могут быть составлены из трех категориальных предложений по два термина в каждом, но для большинства из этих форм вывод не обязательно следует. Лишь немногие из возможных форм оказываются действительными аргументами. В приведенной ниже таблице показаны несколько моделей правильных силлогизмов. (Если вам интересно, как доказать, что они верны, и в других аргументах, которые верны в определенных условиях, вы можете найти дополнительную информацию в ссылках и дополнительной литературе ниже.) Можете ли вы придумать аргументы, используя эти формы?

Все М это Р Все S это М Все S это P	Нет P — M Все S — M Нет S — это P	Некоторые M — это P Все M — это S Некоторые S есть P	Все P — это M Нет M — это S Нет S — это P
Нет M означает P Все S означает M Нет S — это P	Все P — это M Нет S — это M Нет S — это P	Все M — это P Некоторые M — это S Некоторые S есть P	Некоторые P — это M Все M — это S Некоторые S есть P
Все М есть Р Некоторые S есть М Некоторые S есть P	Нет P — это M Некоторые S — это M Некоторые S не являются P	Некоторые M не являются P Все M являются S Некоторые S не являются P	Нет P — это M Некоторые M — это S Некоторые S не являются P
Никакой M не является P Некоторые S не являются M Некоторые S не являются P	Все P являются M Некоторые S не являются M Некоторые S не являются P	Никакой M не является P Некоторые M не являются S Некоторые S не являются P

 

Оценка логического аргумента

Мы знаем, что если дедуктивный аргумент верен и его посылки верны, то его заключение должно быть истинным. Используя это знание, у нас есть способ оценить истинность вывода. Когда кто-то выдвигает аргумент, вы можете проверить его правильность, изучив его посылки и их связь с выводом. Если аргумент действителен, вы должны проверить, верны ли посылки. Но если аргумент недействителен, вы можете отклонить его без необходимости изучения предпосылок.

Давайте посмотрим на высказывание на обычном языке, в котором делается вывод, и попробуем представить его в виде логического аргумента.

[американская бумага] деньги зеленые, как и деревья, поэтому деньги должны расти на деревьях. -психологический пациент, описанный Даффи и Кэмпбеллом. (1994)
Некоторые деньги зеленые. Деревья зеленые. Следовательно, деревья — это деньги.	Некоторые P — это M Все S — это M Все S это P

 

Этот вывод явно неверен.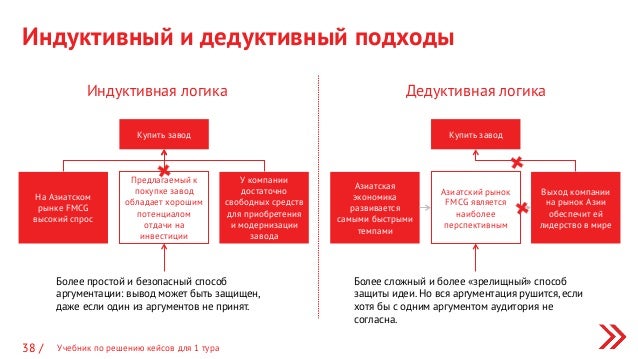 Предпосылки кажутся верными: немного денег — это зеленых. По крайней мере, некоторые деревья зеленые, и, может быть, мы могли бы согласиться с тем, что все деревья зеленые, если правильно определить «зеленый» и «деревья». Но аргумент не является одной из допустимых форм. Вывод не обязательно следует из аргумента, даже если посылки верны. Показ того, что форма аргумента недействительна, может быть полезным способом отклонить аргумент.

Давайте рассмотрим еще один пример обычного языка, который приводит аргумент.

Я не верю, что у нас может быть свобода в философском смысле, ибо мы действуем не только по внешнему принуждению, но и по внутренней необходимости. -Альберт Эйнштейн
Никто по принуждению и необходимости не свободен. Все люди находятся под принуждением и необходимостью. Следовательно, нет свободных людей.	Нет M означает P Все S означает M Нет S — это P

 

Обратите внимание на две вещи о том, что сказал Альберт Эйнштейн. Во-первых, аргумент не полностью сформулирован. Формулируется вывод («мы не можем [не] иметь никакой свободы» в основном означает «нет свободных людей») и формулируется одна из посылок («мы действуем не только по внешнему принуждению, но и по внутренней необходимости»). Но другая посылка, записанная здесь как «Никто по принуждению и необходимости не свободен», прямо не указывается. Это подразумевается в том, что сказал Эйнштейн. На самом деле довольно часто аргументы в повседневной речи оставляют одну из своих предпосылок неявной.

Еще одна вещь, на которую следует обратить внимание в отношении того, что сказал Эйнштейн, это то, что оно следует одному из правильных шаблонов, которые мы рассмотрели ранее. Это означает, что его аргумент верен. Итак, верен ли его вывод? Вывод должен быть истинным, если аргумент верен и посылки верны. Помните, что «истинный» в аргументе означает «точно отражающий реальный мир». Верны ли в этом смысле предпосылки Эйнштейна или нет, может быть вопросом веры.

Импликация

Другим типом дедуктивного аргумента является аргумент из импликации, иногда называемый латинским именем модус поненс . Аргумент из импликации начинается с утверждения if-then , подобного этому.

• Если река узкая, то ее легко перейти.
• Если кто-то проходит мимо, собака лает.

Если первая часть утверждения (часть «если») верна, это означает, что вторая часть (часть «тогда») также верна. Аргумент продолжается утверждением, что часть «если» верна. Это приводит к необходимому выводу, что часть «тогда» должна быть правдой.

Если река узкая, то ее легко перейти.
Река Яда узкая.
Поэтому реку Яда легко пересечь.

Общая структура modus ponens может быть записана следующим образом, где p и q представляют любое утверждение, подобное показанным выше:

Если p, то q
p          
д

Обратное число modus ponens называется modus tollens на латыни или на английском «отрицание следствия». Подобно импликации modus ponens, она начинается с утверждения если-то . Вторая посылка утверждает, что часть «тогда» неверна. Поскольку истинное «если» подразумевает истинное «тогда», ложное «тогда» подразумевает ложное «если».

Если p, то q
не q       
не р

Если кто-то проходит мимо, собака лает.
Собака не лаяла.
Поэтому никто не прошел мимо.

Будьте осторожны с порядком терминов в аргументе из следствия. Истинное «если» подразумевает истинное «тогда», но истинное «тогда» не обязательно подразумевает истинное «если». Утверждение «Если кто-нибудь проходит мимо, собака лает» верно в действительности, по крайней мере, для собаки моего соседа. Он всегда лает на детей, курьеров, соседей или всех, кто проходит мимо. Но если собака лает, это не обязательно означает, что кто-то прошел мимо; Иногда кажется, что эта собака лает без причины.

НЕДЕЙСТВИТЕЛЬНО
Если p, то q q           стр	Если p, то q не p        не д
Если кто-то проходит мимо, собака лает. Собака лаяла. X Значит, кто-то прошел мимо.	Если река узкая, ее легко перейти. Река Сумида не узкая. X Поэтому реку Сумида не так просто пересечь.

 

Мы поговорим об этих видах неверных аргументов позже в курсе, когда будем обсуждать формальные ошибки.

Ссылки, благодарности и дополнительная литература

Copi, Irving. 1962. Введение в логику . Нью-Йорк: Макмиллан.

Даффи, Дж.Д. и Дж.Дж. Кэмпбелл. 1994. «Региональные и префронтальные синдромы: теоретический и клинический обзор». Журнал нейропсихиатрии и клинической нейронауки 6 (4), 379-387.

Ирвин, Л. Ленни. 2010. «Что такое академическое письмо?» в К. Лоу и П. Землянски, Пространства для письма: Чтения по письму . Салон Пресс.

Лагерланд, Хенрик. 2016. «Средневековые теории силлогизма». Стэнфордская энциклопедия философии.

Парсонс, Теренс. 2012. «Традиционная площадь оппозиции». Стэнфордская энциклопедия философии.

Смит, Робин. 2017. «Логика Аристотеля». Стэнфордская энциклопедия философии.

Ван Хевелн, Брэм. 2011. «Критическая мудрость». http://www.cogsci.rpi.edu​/~heuveb​/teaching​/CriticalWisdom​/Introduction.htm

На приведенные здесь объяснения повлияли идеи нескольких людей о логической аргументации и дедуктивных рассуждениях. Популярный учебник Ирвинга Копи « Введение в логику » был важной частью моего обучения логике. «Критическая мудрость» Брама ван Хевелна содержит гораздо больше подробностей о критическом мышлении, аргументации, дедуктивной и индуктивной логике. Стэнфордская энциклопедия философии охватывает не только темы логики, но и многие другие аспекты философии. Мои коллеги с факультета академического письма в Нагойском университете также проводят курсы по логическому мышлению, академическим презентациям и академическому письму, которые меня вдохновили. Некоторые из их материалов и информации также доступны в OpenCourseWare Университета Нагои.

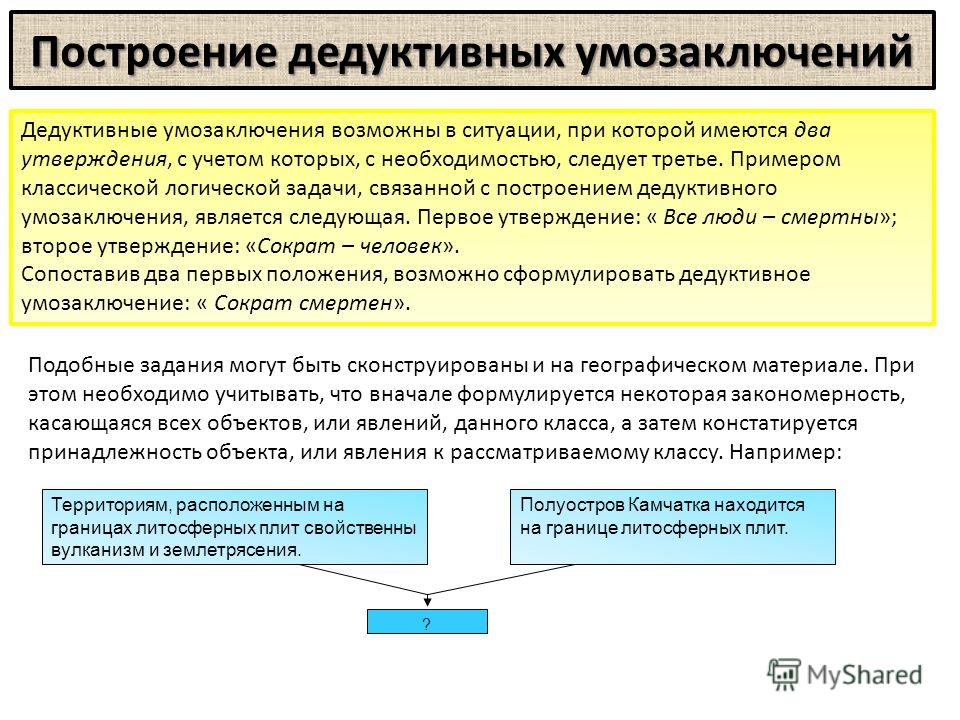
Дедуктивный и индуктивный анализ — разница и сравнение

Дедуктивное рассуждение применяет общие правила для выводов о конкретных случаях. Индуктивное рассуждение наблюдает закономерности в конкретных случаях, чтобы сделать выводы об общих правилах.

Например: Все люди смертны. Джон мужчина. Следовательно, Джон смертен. Это пример правильного дедуктивного рассуждения. С другой стороны, вот пример индуктивного рассуждения: большинство мужчин правши. Джон мужчина. Следовательно, Джон должен быть правшой. Сила этого индуктивного аргумента зависит от процента левшей в популяции. В любом случае вывод вполне может оказаться неверным, поскольку индуктивное рассуждение не гарантирует достоверности выводов.

Что такое дедуктивное мышление?

Дедуктивное рассуждение (логика сверху вниз) отличается от индуктивного рассуждения (логика снизу вверх) и обычно начинается с одного или нескольких общих утверждений или предпосылок для достижения логического заключения. Если посылки верны, заключение должно быть верным. Дедуктивный анализ используется учеными и математиками для доказательства своих гипотез.

Обоснованные или необоснованные аргументы

При дедуктивном рассуждении аргументы могут быть действительными или недействительными, обоснованными или необоснованными. Если логика верна, т. е. вывод вытекает из посылок, то аргументы верны. Однако веские аргументы могут быть обоснованными или необоснованными. Если посылки, используемые в действительном аргументе, верны, то аргумент является обоснованным, в противном случае он несостоятелен.

Например,

1. У всех мужчин по десять пальцев.
2. Джон — мужчина.
3. Следовательно, у Джона десять пальцев.

Этот аргумент логичен и верен. Однако посылка «У всех мужчин по десять пальцев». неверно, потому что некоторые люди рождаются с 11 пальцами. Следовательно, это необоснованный аргумент. Обратите внимание, что все недопустимые аргументы также являются необоснованными.

Типы дедуктивной логики

Закон отстранения

Делается одно условное утверждение и формулируется гипотеза (P). Затем вывод (Q) выводится из утверждения и гипотезы. Например, используя закон отстранения в форме утверждения «если-то»: (1.) Если угол A>90°, то угол А тупой. (2.) А=125°. (3.) Следовательно, угол А тупой.

Закон силлогизма

Закон силлогизма берет два условных утверждения и формирует вывод, комбинируя гипотезу одного утверждения с заключением другого. Например, (1.) Если тормоза откажут, машина не остановится. (2.) Если машина не остановится, произойдет авария. (3.) Следовательно, если тормоза откажут, произойдет несчастный случай.

Мы вывели окончательное утверждение, объединив гипотезу первого утверждения с заключением второго утверждения.

Что такое индуктивное рассуждение?

Индуктивное рассуждение или индукция — это рассуждение из конкретного случая или случаев и вывод общего правила. Это противоречит научному методу. Он делает обобщения, наблюдая закономерности и делая выводы, которые вполне могут быть неверными.

Убедительные и неубедительные аргументы

Сильные аргументы — это аргументы, в которых, если посылка верна, то вывод, скорее всего, будет верным. И наоборот, слабые индуктивные аргументы таковы, что они могут быть ложными, даже если предпосылки, на которых они основаны, верны.

Если аргумент силен и посылки, на которых он основан, верны, то он считается убедительным аргументом. Если аргумент слаб или предпосылки, из которых он вытекает, ложны или недоказаны, то аргумент считается неубедительным.

Например, вот пример сильного аргумента.

1. В морозилке 20 чашек мороженого.
2. 18 из них со вкусом ванили.
3. Следовательно, все чашки мороженого ванильные.

Если в предыдущем аргументе предпосылкой №2 было то, что 2 чашки ванильные, то вывод, что все чашки ванильные, будет основан на слабом аргументе. В любом случае все посылки верны, и вывод может быть неверным, но сила аргумента различна.

Типы индуктивных рассуждений

Обобщение

Обобщение происходит от предпосылки о выборке к заключению о генеральной совокупности. Например, (1.) Выбирается выборка S из совокупности P. Q процент выборки S имеет атрибут A. (2.) Следовательно, Q процент населения P имеет атрибут A.

Статистические силлогизмы

Статистические силлогизмы ведут от обобщения к заключению об индивидууме. Например, (1.) Доля Q населения P имеет атрибут A. (2.) Индивидуум X является членом P. (3.) Следовательно, существует вероятность, соответствующая Q, что X имеет атрибут A .

Дополнительные примеры

Примеры дедуктивного рассуждения

Четырехугольник ABCD имеет стороны AB ll CD (параллельны) и стороны BC ll AD. Докажите, что это параллелограмм. Чтобы доказать это, мы должны использовать общие утверждения, данные о четырехугольнике, и прийти к логическому заключению.

Другим примером дедуктивной логики является следующее рассуждение:

1. Все лабрадоры-ретриверы — собаки.
2. Некоторые лабрадоры-ретриверы являются домашними животными.
3. Поэтому некоторые собаки являются домашними животными.

Примеры индуктивных рассуждений

Если три следующих друг за другом фигуры — треугольник, квадрат и пятиугольник, какая из них будет следующей? Если рассуждающий наблюдает закономерность, он заметит, что количество сторон в фигуре увеличивается на единицу, и поэтому обобщение этой закономерности приведет его к выводу, что следующей фигурой в последовательности будет шестиугольник.

Применение индуктивных и дедуктивных рассуждений

• Дедукцию также можно временно использовать для проверки индукции, применяя ее в другом месте.
• Хороший научный закон очень обобщен, как и в индуктивных рассуждениях, и может применяться во многих ситуациях для объяснения других явлений.
• Дедуктивное рассуждение используется для вывода многих экспериментов и доказательства общего правила.

Предвзятость

Индуктивное рассуждение также известно как построение гипотез, поскольку любые сделанные выводы основаны на текущих знаниях и прогнозах. Как и в случае дедуктивных аргументов, предубеждения могут исказить правильное применение индуктивного аргумента, что не позволяет рассуждающему сделать наиболее логичный вывод на основе подсказок.

Эвристика доступности

Эвристика доступности приводит к тому, что автор рассуждений в первую очередь зависит от легкодоступной информации. Люди склонны полагаться на информацию, которая легко доступна в окружающем их мире. Это может привести к предвзятости в индуктивных рассуждениях.

Смещение подтверждения

Смещение подтверждения основано на естественной склонности подтверждать, а не отрицать текущую гипотезу. Например, несколько столетий считалось, что Солнце и планеты вращаются вокруг Земли.