Формальная логика связана с: Логика формальная это

Формальная логика в инженерной деятельности

Библиографическое описание:

Авдеюк, О. А. Формальная логика в инженерной деятельности / О. А. Авдеюк, А. А. Соловьев, Д. Н. Авдеюк. — Текст : непосредственный // Молодой ученый. — 2013. — № 3 (50). — С. 309-311. — URL: https://moluch.ru/archive/50/6413/ (дата обращения: 18.02.2023).

Важной проблемой современной науки становится назревшая необходимость расширения роли междисциплинарных исследований. Особенно перспективными в этом ключе представляются функциональные связи гуманитарной и технической областей. Наука логика, на наш взгляд, является одной из таких отраслей знания, которые в значительной степени способствуют конструктивному диалогу, а также эффективному взаимодействию социально-гуманитарной и информационно-технической сфер современного общества.

Традиционно формальная логика считается учением о формах и законах человеческого мышления, отрывающим исследование этих форм от их содержания (природы и общества).

Иногда логику рассматривают как особую философскую дисциплину, преследующую цель изучить возможности интеллектуальной познавательной деятельности (здесь логика напрямую пересекается с гносеологией). Отдельными научными школами логика рассматривается как наука о способах доказательства и опровержения.

В качестве самостоятельной области знания логика оформилась в трудах Аристотеля, который систематизировал известные до него сведения, и эта система стала впоследствии называться формальной или Аристотелевой логикой. Описанные древнегреческим мыслителем правила вывода (силлогизмы) были вплоть до XVII в. основным логическим инструментарием. Многие поколения студентов изучали силлогизмы наизусть, так как они считались нормативной формой рациональных процессов мышления.

По мере развития математики стало ясно, что формальная логика обладает рядом недостатков, в частности, не формализована, поэтому в конце XVII в.

немецкий ученый Г. Лейбниц предложил понятия логики обозначить символами, которые соединялись бы по особым правилам. Это позволяло всякое рассуждение заменить математическим выражением.

Одна из первых значимых реализаций идей Лейбница принадлежит ирландскому математику Дж. Булю, который применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые фундаментальные законы мышления. Именно благодаря введению символов была получена основа для создания новой науки — математической логики.

Математическая логика — современный вид формальной логики, то есть науки, изучающей умозаключения с точки зрения их формального построения [14]. Данная наука не сразу нашла приложение в технических исследованиях и считалась едва ли не «экзотической теорией». Однако в начале ХХ века, в связи с развитием электроники, ее положения нашли применение в описании функционирования и разработке различных электронных схем, а позже стали использоваться и для решения других инженерных задач.

Рассмотрим некоторые из них.

В 1910 г. отечественный ученый П. Эренфест впервые предложил использовать аппарат формальной логики в технике. С тех пор логика высказываний успешно применяется в теории электрических цепей, в частности при исследовании релейно-контактных схем [6, 12, 14]. Действительно, любой параллельно-контактной схеме можно поставить в соответствие логическую формулу, описывающую работу этой схемы. Затем в результате применения основных равносильностей логики высказываний, можно упростить схему, построив эквивалентную исходной, но с меньшим количеством элементов.

Аппарат математической логики широко используется для описания работы и в проектировании разнообразных частей компьютеров (вентили, триггеры, сумматоры, дешифраторы, шифраторы, элементы памяти, арифметико-логическое устройство процессора) [6, 7, 12]. Различные электронные схемы (их комбинации) на логическом уровне могут быть описаны с помощью логических операторов: фактически это элементарная логическая функция, с помощью которой описывается работа схемы в целом. Такое операторное описание электронных схем позволяет абстрагироваться от физической природы конкретных электронных элементов, но при этом осуществлять их анализ. Чтобы получить значение функции на выходе какой-либо схемы, достаточно записать эту зависимость в виде логических операторов, связанных между собой в соответствии с выполняемой функцией. Задачу синтеза электронных схем можно формулировать следующим образом: при заданных входных переменных и известной выходной функции, проектируется логическое устройство, которое эту функцию реализует. На последнем этапе синтеза логическую функцию сопоставляют с некоторыми физическими элементами и логическую схему заменяют структурной схемой, состоящей из физических элементов. Так удается соединить математическую задачу синтеза логической схемы с инженерной задачей проектирования схемы электронной.

Логический вывод применяется также при оценке переходных процессов в электронных системах (интегральных схемах), реализующих субмикронную технологию [2]. К одной из основных проблем в таких системах относится проблема возникновения ложной информации, обусловленной неодновременным переключением входных каналов из-за задержек сигналов в каналах связи. Для решения этой задачи специалист может применить один из разделов математической логики — теорию трасс, которая позволяет вычислить распределение трасс в булевом пространстве, определяющее объективные причины возникновения ложной информации в интегральной схеме.

Уже на протяжении нескольких десятилетий связь между математической логикой и компьютерами лежит в основе используемой в ЭВМ двоичной системе счисления.

В языках программирования любого уровня (машинных, машинно-ориентированных, машинно-независимых) обязательно содержатся логические операторы, и даже существует целый класс логических языков (например, Prolog, Lisp). К основным моделям программирования относится логическое программирование, которое представляет собой парадигму программирования, основанную на автоматическом доказательстве теорем с использованием механизмов логического вывода информации на основе заданных фактов и правил вывода.

Логические языки и логическое программирование широко используются для создания баз знаний, экспертных систем и исследований в сфере искусственного интеллекта на основе логических моделей баз знаний и логических процедур вывода и принятия решений [8].

Стало активно развиваться такое направление как математическая лингвистика, направленное на разработку формального аппарата для описания строения как искусственных, так и естественных и языков [1]. В основу этой дисциплины также заложен аппарат математической логики.

Логический вывод широко используется в современных информационных технологиях и при разработке экспертных систем. В. А. Горбатов, например, рассматривает вариант использования логического вывода в экспертных системах при прогнозировании месторождений полезных ископаемых. В качестве исходных данных выступает апостериорная информация, полученная в результате геологической разведки одного из горных районов, целью которой является прогнозирование месторождения рудного тела.

Первичными термами обозначают искомые величины. Затем, применяя введенные обозначения и секвенциальное исчисление (секвенция записывается в виде антецедент → сукцедент — это термины схоластической логики), записывают систему секвенций. На следующем этапе, используя свойство критичности покрытия двоичных таблиц, по специальному алгоритму, получают вывод о зоне с определенными углами азимута падения залегания рудного тела.

В решении задачи организации видеонаблюдения за этапами некоторого производственного процесса применяется аппарат теории графов. В этом случае вершины графа представляют собой технологические модули гибкого автоматизированного процесса, за которым должно осуществляться непрерывное наблюдение, а две вершины графа соединены ребром, если соответствующие им модули можно наблюдать, находясь около одного из них. Требуется так расставить телекамеры, чтобы оператор, находящийся у монитора, мог наблюдать за всеми модулями, но при этом число телекамер было бы минимальным.

На языке теории графов это означает, что надо определить вершинное число внешней устойчивости данного графа, для чего успешно применяют методы Магу, также основанные на аппарате математической логики [13].

В заключение следует отметить следующее: несмотря на то, что за многие столетия логика Аристотеля претерпела существенные преобразования, многие ученые сходятся в том, что идея формальной логики восходит к трудам ее древнегреческого создателя. Мы полагаем, что справедливо указывает В. В. Морозов: «логика Аристотеля — закономерное звено в историческом развитии древнегреческой логики. Она находится в теснейшей связи с состоянием научного знания того времени. Несмотря на то, что Аристотель много занимался естествознанием и написал специальные научные трактаты по физике и зоологии, а математическим наукам не посвятил ни одного своего сочинения, тем не менее, на его логике лежит печать не естественнонаучного, а математического мышления» [10].

Поэтому можно утверждать, что именно Аристотель сделал первый существенный вклад в развития современного вида логики (математической) а, значит, его научные работы имеют большое значение в решении многих современных технических задач.

Литература:

1. Аляев Ю. А. Дискретная математика и математическая логика: учебник / Ю. А. Аляев, С. Ф. Тюрин // М.: Финансы и статистика, 2006. — 386 с.
2. Горбатов В. А. Фундаментальные основы дискретной математики. Информационная математика. — М.: Наука. Физматидат, 2000.- 544 с.
3. Горелов А. А. Основы философии: Учебное пособие / Москва: Издательский центр «Академия», 2007 г. — 256 с.
4. Горохов В. Г. Логика и техника: от теории электрических цепей к наносистемотехнике [Электронный ресурс: http://iph.ras.ru/uplfile/logic/log18/LI-18_Gorokhov. pdf]. Дата обращения: 16. 02. 2013 г.
5. Информатика: Энциклопедический словарь для начинающих / Сост. Д. А. Поспелов. — М.: Педагогика-Пресс, 1994. — 352 с.
6. Лихтарникова Л. М. Математическая логика. Курс лекций / Л. М. Лихтарникова, Т. Г. Сукачева // СПб.: Издательство «Лань», 1998. — 288 с.
7. Логические основы ЭВМ [Электронный ресурс: http://www.inf1.info/book/export/html/210]. Дата обращения: 16. 02. 2013 г.
8. Логическое программирование. [Электронный ресурс: http://www. tadviser. ru / index.php]. Дата обращения: 16. 02. 2013 г.
9. Логика Аристотеля. [Электронный ресурс: http://www. plam.ru/ nauchlit/ istorija_logiki/p4.php]. Дата обращения: 16. 02. 2013 г.
10. Морозов В. В. История инженерной деятельности. Курс лекция для студентов всех специальностей дневного и заочного обучения / В. В. Морозов, В. И. Николаенко // Харьков: НТУ «ХПИ», 2007. — 336с.
11. Муха Ю. П. Информатика. Часть 1. Теория информации и кодирования. Конспект лекций по дисциплине «Информатика»: учеб. пособие / Ю. П. Муха, О. А. Авдеюк, А. С. Новицкий // ВолгГТУ. — Волгоград, 2004. — 76 с.
12. Муха Ю. П. Математическая логика и теория алгоритмов: учеб. пособие / Ю. П. Муха, О. А. Авдеюк. — 2-е изд., стер. — Волгоград: ИУНЛ ВолгГТУ,2011.– 92 с.
13. Муха Ю. П. Дискретная математика. Конспект лекций: учеб. пособие / Ю. П. Муха, О. А. Авдеюк / ВолгГТУ. — Волгоград, 2005. — 104 с.
14. Нефедов В. Н. Курс дискретной математики: учеб. пособие / В. Н. Нефедов, В. А. Осипова// М.: Изд-во МАИ, 1992. — 264 с.
15. Никитин А. В. О логике и логической машине [Электронный ресурс: http://andrejnikitin.narod.ru/logik_mashin.htm#_Toc324237270]. Дата обращения: 16. 02. 2013 г.
16. Фудзисава Т. Математика для радиоинженеров: Теория дискретных структур / Т. Фудзисава, Т. Кассами // М.: Радио с связь, 1984. — 240 с.

Чем интуитивная логика отличается от формальной и как правильно делать умозаключения из утверждений «все мужики козлы» и «некоторые бабы дуры» — Нож

Почему логика — квадратная

Логика называется формальной потому, что работает с формой, а не содержанием, то есть с тем, как устроены предложения и как они между собой связаны. Это полезно тем, что мы можем отстраниться от смысла предложений, которые могут задевать наши чувства, и сделать правильное умозаключение без эмоционального влияния.

Давайте начнем с простых умозаключений, которые принято называть «умозаключениями по логическому квадрату».

Логика (на нашем начальном уровне) имеет дело с утвердительным предложениями — простыми суждениями, которые по двум признакам делятся на четыре группы.

1-й признак: количество

По количеству суждения делятся на общие и частные.

«Все мужики козлы» — общее суждение.

«Некоторые бабы дуры» — частное суждение.

2-й признак: качество

По качеству бывают утвердительные и отрицательные суждения.

«Мой муж козел» — утвердительное суждение.

«Моя жена не дура» — отрицательное суждение.

Если мы объединим эти два признака, то получим четыре типа суждений, а в скобках укажем их классические обозначения:

«Все люди смертны» — общеутвердительные (A).

«Ни одна панацея не работает» — общеотрицательные (E).

«Некоторые методы доказательной медицины работают» — частноутвердительные (I).

«Некоторые методы народной медицины не работают» — частноотрицательные (O).

Запомнить символьное обозначение классов суждений легко, если знать их происхождение от латинских слов “affirno” — утверждать и “nego” — отрицать, из которых были взяты гласные: первые — для общих суждений, вторые — для частных.

Вы уже догадались, что углы квадрата — четыре типа суждений. Часто его рисуют вот так:

Зачем нам нужен этот квадрат? Очень просто: он показывает, в каких отношениях находятся суждения разных классов. То есть с его помощью мы можем проверять себя, правильно ли мы делаем преобразования суждений, и выяснять, куда именно закралась ошибка.

Все или некоторые? Делаем правильные выводы

Обычно мы делаем логические преобразования со сложными для анализа суждениями. Но мы рассмотрим силу логического квадрата на примере содержательно простых суждений.

Предположим, что мы думаем так:

«Все мужики козлы».

Какие выводы мы можем из этого сделать? Это общеутвердительное (А) суждение, следовательно, мы можем сказать, что:

«Некоторые мужики козлы»

— это тоже верное суждение, так как оно частноутвердительное (I) и (смотрим на квадрат) находится в отношении подчинения с A.  Все отрицательные суждения при этом будут ложными, неправильными, так как они будут контрарными (общеотрицательные E) и контрадикторными (частноотрицательные O) по отношению к изначальному суждению (общеутвердительные A). То есть неправильно будет сказать «некоторые мужики — не козлы».

Несколько интереснее получается, если у нас исходное суждение частноутвердительное:

«Некоторые бабы дуры».

Можно ли из этого сделать вывод, что все бабы дуры? Нет, из частного нельзя вывести общее, только наоборот: отношение подчинения в квадрате — одностороннее! Вот так-то.

А что с отрицательными суждениями?

Можно ли сделать вывод, что если некоторые бабы дуры, то среди баб встречаются умные? То есть верно ли частноотрицательное суждение, если верно частноутвердительное?

Казалось бы, это так и просится: если только часть грибов съедобные, то ясно же, что есть какие-то несъедобные грибы. Или если некоторые лебеди белые, то часто кажется, что предполагается наличие каких-то других лебедей.

Однако с точки зрения формальной логики это не так! Отношение субконтрарности означает, что суждения не могут быть одновременно ложными — и только. То есть не может быть такого, что неверны оба утверждения: и «некоторые бабы дуры», и «некоторые бабы не дуры». Такого не может быть, а вот другие сочетания возможны: мы говорим, что некоторые бабы дуры, а это может означать, что на самом деле все они дуры, просто мы этого не знаем или нам сейчас это неважно. А может быть, что действительно есть не дуры. Надо наблюдать — но это уже не про логику, а про жизнь.

Никто или некоторые?

Вот, например, исходное общеотрицательное суждение, которое можно сделать из отрицания знаменитого мифа о том, что люди используют свой мозг только на 10 %.

«Никто не использует мозг на 10 %».

Оно дает нам на самом деле довольно мало информации. Мы можем вывести из него «некоторые не используют мозг на 10 %». По-русски эту звучит весьма неоднозначно — и это еще одна проблема использования естественного языка в формальной логике, но об этом в другой раз.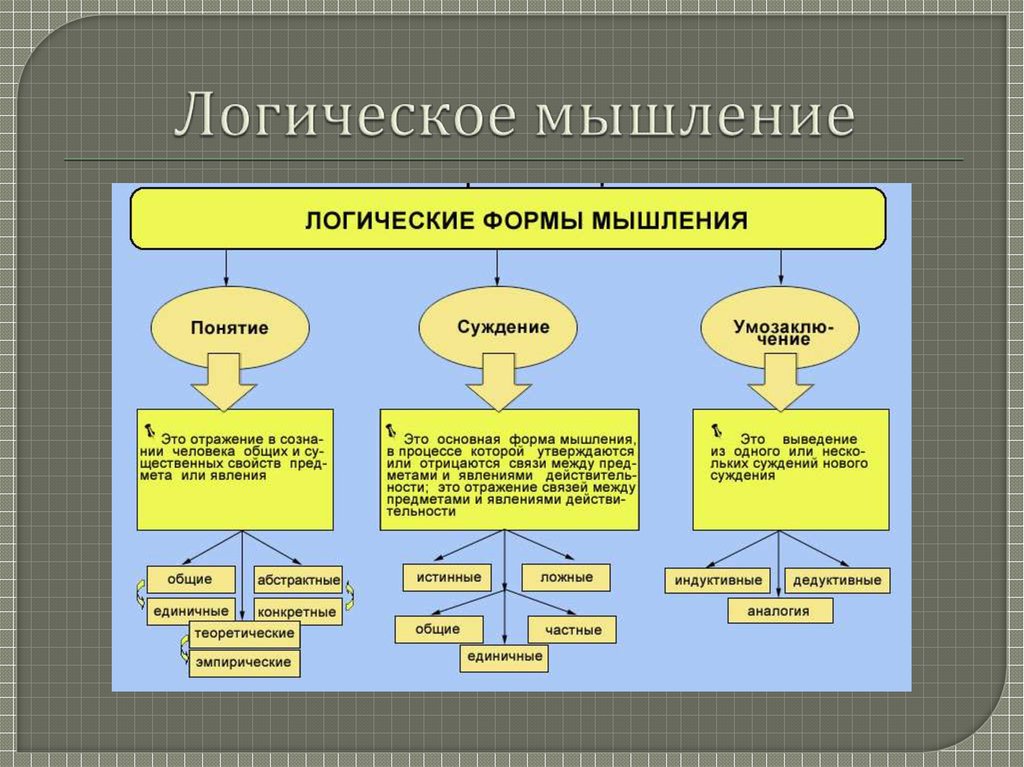

Возьмем за изначальное суждение частноотрицательное:

«Некоторые таблетки не лечат».

Какой вывод из этого можно сделать? Некоторые делают вывод, что врачи травят людей таблетками и нужно лечиться чем-то «натуральным». На самом деле можно сделать лишь один вывод: общеутвердительное суждение «все таблетки лечат» не является истинным — что никогда не вызывало сомнений, особенно учитывая, что медикаменты довольно часто употребляют без рекомендации врачей.

Для закрепления расшифруем связи в квадрате, которые еще не называли, и перейдем к рассмотрению некоторых типичных ошибок, связанных с умозаключениями по логическому квадрату:

Контрарность — суждения в этом отношении могут быть одновременно ложными либо одно из них истинное, другое ложное, одновременно истинными быть не могут.

Субконтрарность — суждения могут быть одновременно истинными либо одно из двух истинное, оба ложными не могут быть.

Контрадикторность — одно из двух суждений обязательно истинное.

Мне помогло — и вам поможет, или Поспешное обобщение

Очень часто можно встретить примерно такие высказывания:

«Мне чай из иван-чая помог, советую вам пить каждый день иван-чай — тоже всё будет просто отлично!»

Что не так с этим умозаключением?

Мы не будем разбирать фактическую ошибку (иван-чай, тем более высушенный и заваренный, имеет мало чего полезного) или часто упоминающуюся ошибку «„после“ — не значит „вследствие“», а поговорим исключительно об ошибке, связанной с логическим квадратом.

Для этого нам из исходных предложений нужно получить формально-логические суждения.

«Некоторым (мне, моим детям, мужу) помог иван-чай».

Следовательно:

«Всем поможет иван-чай».

Почему мы делаем первое суждение частноутвердительным, а второе — общеутвердительным? В первом случае речь идет об одном или нескольких людях, которым помог иван-чай, то есть не о целом классе предметов, не о всём множестве, не обо всех людях. Во втором же случае речь идет о случайном представителе людей, потому это можно принять за целое множество людей, которые имеют то же заболевание, что и тот, кому помогло, или вообще всех людей, если речь идет о панацее или повышении, стимуляции иммунитета, например. В некоторых случаях говорят именно так: мне помогло — значит, и всем поможет. Так мы и делаем общеутвердительное суждение.

Уже на этом этапе видна проблема обсуждаемого умозаключения: от частноутвердительного суждения происходит переход к общеутвердительному, что не соответствует их отношению подчинения.

Такая ошибка называется поспешное обобщение — весьма распространенная ошибка, особенность которой в том, что она не всегда приводит к ложным результатам, потому людям иногда кажется, что так можно делать.

Все бабы дуры, я одна королева!

Думаю, вы встречали подобные высказывания:

«Никто не умеет ездить, я один король дороги!»

Это класс довольно часто встречающихся высказываний. Давайте разберемся, в чем они ошибочны.

Основная ошибка связана с тем, что люди исключают себя из множества: да, я нарушаю правила дорожного движения, но я же не такой, как все остальные.

Людям не хочется причислять себя группам людей — хотя у них в действительности нет оснований для исключения из них. Основную роль в этом необоснованном исключении играют эмоции, связанные с чем-то неприятным.

Красивый и развернутый пример такого процесса самисключиения мы можем найти, например, у Льва Николаевича Толстого в повести «Смерть Ивана Ильича»:

«В глубине души Иван Ильич знал, что он умирает, но он не только не привык к этому, но просто не понимал, никак не мог понять этого.

Тот пример силлогизма, которому он учился в логике Кизеветера: Кай — человек, люди смертны, потому Кай смертен, казался ему во всю его жизнь правильным только по отношению к Каю, но никак не к нему. То был Кай-человек, вообще человек, и это было совершенно справедливо; но он был не Кай и не вообще человек, а он всегда был совсем, совсем особенное от всех других существо; он был Ваня с мама, папа, с Митей и Володей, с игрушками, кучером, с няней, потом с Катенькой, со всеми радостями, горестями, восторгами детства, юности, молодости. Разве для Кая был тот запах кожаного полосками мячика, который так любил Ваня! Разве Кай целовал так руку матери и разве для Кая так шуршал шелк складок платья матери? Разве он бунтовал за пирожки в Правоведении? Разве Кай так был влюблен? Разве Кай так мог вести заседание?

И Кай точно смертен, и ему правильно умирать, но мне, Ване, Ивану Ильичу, со всеми моими чувствами, мыслями, — мне это другое дело. И не может быть, чтобы мне следовало умирать. Это было бы слишком ужасно».

Замечали за собой похожие рассуждения?

«Какая вредная еда. Все, кто её едят, толстеют. Но со мной — совсем другая история!»

Как все подобные мысли связаны с формальной логикой? Если переводить эти рассуждения в необходимую для нас форму, то получится, что в них человек пытается одновременно считать истинными суждения двух типов:

A — общеутвердительное («Все мужчины — агенты патриархата»)

и O — частноотрицательное («Некоторые (я) не агенты патриархата, а профеминисты»).

Могут ли они быть одновременно истинными?

Нет, не могут, так как находятся в отношении контрадикторности: это противоречащие друг другу суждения, которые не могут быть одновременно истинными.

Мы говорили, что при контрадикторности только одно суждение может быть истинным, более того, должно быть истинным. Сами посудите: если все лебеди белые, то некоторые из них не могут быть черными, а если всё же нашли в Австралии черных лебедей, то уже не все лебеди будут белыми.

Можно попробовать обосновать утверждение, что я действительно не такой/такая, как другие, потому что на меня не действуют общие правила («Все мужчины, воспитанные в патриархате, — угнетатели, а я — мужчина, воспитанный феминисткой»).

С одной стороны, это уже не логический аспект, а фактологический, с другой — зачастую совершенно несложно, если избавиться от эмоций, разобраться с тем, что вы не выделяетесь в отдельный класс. Вот если бы вы были единственным чернокожим в толпе белых — тогда было бы хоть какое-то основание для выделения вас в отдельную группу, да и то современные исследования показывают, что основное различие между расами — именно что цветовое.

Эмоции — один из главных врагов логического мышления, именно они очень часто мешают нам принимать взвешенные логические решения.

Мы это видели и в первой разобранной ошибке, и особенно во второй. Будет эта же проблема и в третьей ошибке.

Иногда не иногда!

— Дорогой, ты иногда поступаешь так умно!
— Ага, значит, иногда я поступаю так глупо, да?

Думаю, что вы сталкивались с чем-то подобным в своей жизни, причем тут не важен пол: такой ответ можно услышать и от девушки, и от парня, но правильный ли сделан вывод?

Для того чтобы сказать однозначно, так, чтобы результат был общий для всех подобных ситуаций, чтобы не нужно было каждый раз подбирать фактические аргументы, что бывает сложно, мы приведем рассуждения в безэмоциональный формальный вид. Сделать это не так просто, и в процессе преобразования у нас получится довольно сильно отличающиеся по форме предложения:

— Дорогой, некоторые твои поступки умны.
— Ага, следовательно, некоторые мои поступки не являются умными.

Надеюсь, вы уже натренировали свой глаз и легко поняли, какого типа эти суждения: они оба частные, но первое утвердительное, а второе отрицательное. Тут есть некоторая тонкость при анализе: можно исходное суждение видоизменить так, что получится частноутвердительное суждение:

«Ага, следовательно, некоторые мои поступки являются не умными».

Для работы по логическому квадрату нам важно, чтобы у двух сравниваемых суждений были бы одинаковые части. Так, в первом суждении у нас в отношении находятся «твои поступки» и «умны», потому во втором должны быть они же, а не «твои поступки» и «не умны». Может меняться связка с «являются» на «не являются» — это показывает смену типа суждения, но не меняет содержания, сути. Именно поэтому нам нужно получить суждение: «Некоторые мои поступки не являются умными».

Что же мы можем сказать про эти суждения?

Если мы вспомним логический квадрат, то выясним, что частные суждения находятся в отношении субконтрарности, то есть могут быть одновременно истинными, но не могут быть одновременно ложными. При этом нужно помнить, что может так быть, что только одно из этих двух суждений истинное. Это приводит к тому, что если мы имеем одно истинное частное суждение — утвердительное, как в нашем примере, — то мы не можем однозначно сказать, является ли субконтрарное — частноотрицательное суждение — истинным или ложным.

«Некоторые автомобили загрязняют атмосферу».

Можем ли мы из этого сделать вывод, что некоторые автомобили не загрязняют?

Или вот:

«Некоторые гомеопатические препараты не содержат активного компонента».

Можно ли из этого сделать вывод, что в некоторых гомеопатических препаратах всё-таки есть действующее вещество? (Спойлер: нет, не должно быть, иначе они не гомеопатические).

Вот пример риторического приема, когда вы говорите оппоненту:

«А вот тут вы правы!»

Это может быть воспринято им (или теми, кто наблюдает за вашим спором) эмоционально: как будто в других местах беседы он был неправ и только тут вы готовы с ним, так уж и быть, согласиться. С точки зрения логики, как мы обсуждали выше, тут нет ни ошибки, ни указания на то, что оппонент был неправ в остальных местах. Что вы ему и объясните, когда он возмутится и выразит несогласие, показав себя не с лучшей стороны.

Так иногда можно использовать ошибки, которые люди допускают в формальной логике из-за эмоций, себе на пользу.

---

Как видите, найти логически правильный ответ достаточно легко, даже если не знаешь точного логического объяснения. Но когда в дело вмешиваются эмоции, то дойти до правильного вывода — даже зная формальную логику — не так-то просто.

Знание описанных выше простых правил позволяет четко и просто выявить логические пробелы в собственных и чужих умозаключениях и спокойно, аргументированно указать на них.

Формальная логика и структура музыки — Текущий журнал исследований, том. 3

Загрузить документ в формате pdf

 

Divinevictory Amayo, Howard Community College, 2019, UMBC

Под руководством доктора Майка Лонга , Howard Community College

 

Аннотация

 

Формальная логика обеспечивает основу для формального математического доказательства в математике высокого уровня. С другой стороны, музыка, одно из изобразительных искусств, где вокальные и инструментальные звуки сочетаются таким образом, чтобы развлекать публику и бросать вызов исполнителям. В течение некоторого времени музыка и математика были связаны, в частности, посредством анализа звуковых волн, который требует тригонометрии. Оказывается, музыка и формальная логика тоже могут быть связаны. Это привело к вопросу: когда музыкальные пассажи эквивалентны так же, как логически эквивалентны математические утверждения? С помощью музыкального анализа и использования основных формальных логических понятий обратного, обратного и контрапозитивного мы исследуем, когда существуют эквивалентности. Оказывается, в некоторых случаях эквивалентности действительно существуют, и поэтому музыкальные отрывки эквивалентны в том смысле, в каком эквивалентны логические высказывания. Но есть много случаев, когда музыкальные пассажи, которые могут показаться логически эквивалентными, таковыми не являются, и мы исследуем и математически объясняем, почему они не эквивалентны.

Введение  

« Математика» — слово, которое вселяет страх в сердца многих студентов. Гитара – инструмент с богатой историей и еще более насыщенным звучанием, любимый миллионами людей по всему миру. Что общего у этих двух вещей? Весной 2018 года я не знал, и мне было все равно. Я был студентом, пытающимся избавиться от всей ужасной математики, необходимой для его специальности, и начинающим гитаристом. Итак, когда я открыл рот, чтобы сказать моему профессору дискретной математики (который является моим наставником в этом проекте) о моей неприязни к его области, я не предвидел, что он заставит меня принять вызов, который попытается изменить мое мнение о математика. Задача приняла форму исследовательского проекта, который должен был углубиться в темы формальной логики, затронутые на моем уроке дискретной математики, и объединить эти темы с моими растущими знаниями и пониманием мира музыки через гитару.

Фон

Есть некоторые общие структуры формальной логики, которые необходимо ввести, чтобы начать обсуждение этого исследования. Первый — это условный оператор «если/то» или «если p , то q », где каждое из p и q представляет утверждения. Утверждения в формальной логике идентифицируются как предложения, которые либо истинны, либо ложны. Символически «если p , то q » представляется как . Вторая структура, которую следует рассмотреть, просто меняет порядок этих операторов на противоположный, который мы запишем как . Это известно как «обратное». Третья структура, которую следует рассмотреть, включает в себя добавление отрицаний к обоим утверждениям, которые мы запишем как . Это известно как «инверсия», когда волнистая линия перед цифрой p и q представляют собой отрицание утверждения или, более неформально, «не». Четвертая структура меняет порядок операторов, а также добавляет отрицания, которые мы записали бы как . Это известно как «контрапозитив». Исходное условное и контрапозитивное имеют важную характеристику в формальной логике, а именно то, что они логически эквивалентны. Точно так же инверсия и инверсия логически эквивалентны. Что именно означает быть логически эквивалентным?

• Два условных утверждения (если / то) имеют одинаковые таблицы истинности или таблицы, используемые в математической логике для определения достоверности утверждений
• Два условных утверждения (если / то) могут быть доказаны друг из друга с использованием методов формального математического доказательства

В таблице 1 сравниваются условные операторы.

Таблица 1:   Сравнение условных операторов

Имя условного оператора:	Символы:	Пример:	Логически эквивалентен:
Оригинал выписки		Если загорится красный свет, я остановлюсь.	Противоположный
Конверс		Если я остановлюсь, загорится красный свет.	Обратный
Обратный		Если свет не красный, то я не остановлюсь.	Конверс
Противоположное		Если я не остановлюсь, значит, горит не красный свет.	Исходное заявление

Нечто подобное существует в структуре музыки. Эти структуры были замечены в музыке, сочиняемой с 1500-х годов в Европе, но стали заметными в серийной композиции в конце 1800-х и начале 1900-х годов, снова в Европе [1].

 

Сначала мы рассматриваем отрывок или музыкальную строку как нашу базовую структуру, которую мы можем рассматривать как аналогичную исходному условному оператору в формальной логике (рис. 1 и табл. 2). Вторая музыкальная структура, которую следует рассмотреть, — это «ретроградная». В музыке ретроградом исходной строки или пассажа является просто исходная строка или пассаж, играемый в обратном порядке, начиная с последней ноты или остатка исходного пассажа и заканчивая первой нотой или остатком исходного пассажа. Это было бы похоже на обратное в формальной логике, где порядок обратный. Третьей музыкальной структурой, которую следует рассмотреть, является «инверсия». В музыке инверсия исходной строки или пассажа создается буквально переворачиванием нот вверх ногами на нотном стане, изменяя контур музыки. В этой структуре первая нота такая же, как и в исходной строке или музыкальном отрывке (некоторые композиторы немного модифицировали это определение и использовали другую начальную ноту, но в этом исследовании начальная нота не будет изменена). Эта структура была бы похожа на инверсию в формальной логике, которая является отрицанием или противоположностью исходных утверждений. Последняя структура, которую следует рассмотреть, — это «ретроградная инверсия». При ретроградной инверсии исходная строка или пассаж переворачивается на нотном стане, как при инверсии, а затем порядок меняется на обратный, как при ретроградной (ретроградная инверсия чаще всего является ретроградной инверсией, но некоторые композиторы конвертируют в противоположную сторону). порядок, который имеет разные результаты). В этой структуре первая нота совпадает с последней нотой инверсии, а последняя нота совпадает с первой нотой исходного отрывка. Эта структура была бы похожа на контрапозитив в формальной логике, который является отрицанием или противоположностью исходных утверждений с измененным порядком.

Гипотеза  

Мы предположили, что исходное музыкальное высказывание и ретроградная инверсия будут одинаковыми по ритму и тональности, тождественным совпадением точно так же, как исходное высказывание и контрапозитив в формальной логике логически эквивалентны. Эта идея возникла из-за того, что исходная строка или отрывок музыки и ретроградная инверсия, по-видимому, были эквивалентны точно так же, как эквивалентны исходное утверждение и противопоставление в формальной логике.  

Начальные результаты

Мы уже показали параллели между исходным утверждением и исходной строкой или отрывком музыки, а также ретроградной инверсией и контрапозитивом. Однако, изучая наши первые музыкальные произведения, мы быстро поняли, что наша гипотеза неверна. Ритм и тональность исходной строки или музыкального отрывка и ретроградной инверсии были разными. В результате мы изменили идею этой исследовательской работы, чтобы предложить рабочее определение «музыкальной эквивалентности» на параллельную «логическую эквивалентность».  

Определение музыкальной эквивалентности  

Был создан простой музыкальный отрывок с тремя четвертными нотами и четвертной паузой (рис. 1), чтобы лучше описать музыкальные структуры: исходная музыкальная линия или отрывок, за которым следует ретроградная инверсия и, наконец, ретроградная инверсия. Кружки с прикрепленными вертикальными линиями — это ноты, которые сообщают музыканту, какая высота звука должна звучать и как долго. Символы типа французских скобок — это паузы, которые говорят музыканту не играть в течение определенного периода времени. Этот простой отрывок содержит четыре такта. Вертикальные линии указывают, где начинается каждый новый такт.

 

Рисунок 1 : Музыкальный отрывок из четырех тактов

 

Таблица 2 разбивает простое музыкальное произведение на четыре части по такту. Таблица также добавляет сравнения к формальной логике. Эта таблица также облегчает понимание того, почему была выдвинута первая гипотеза.

Таблица 2:  Сравнение условных операторов и музыкальных структур. Обратите внимание, что символы добавляются в инверсии и ретроградной инверсии. Это делается для того, чтобы шаги между нотами были одинаковыми. В тексте обсуждается понятие «шаг».

Музыка
Имя	Оригинальная строка или музыкальное высказывание	Ретроградный	Инверсия	Ретроградная инверсия
Параллельность в формальной логике	Условное заявление	Конверс	Обратный	Противоположный
Символы
Эквивалент	Противоположный	Обратный	Конверс	Условное заявление

 

Чтобы понять обсуждение «музыкальной эквивалентности», полезно понять, как в музыке определяются «шаги». Самый простой способ понять шаги в музыке — посмотреть на клавиатуру фортепиано. Две белые клавиши, между которыми нет черных клавиш, разделены полушагом. Две белые клавиши, между которыми находится черная клавиша, разделены целым шагом. Чтобы еще больше разбить это, движение от белой клавиши к соседней черной клавише составляет полшага, а затем от черной клавиши к следующей белой клавише также является полушагом. Точно так же две черные клавиши, между которыми находится белая клавиша, разделены целым шагом. Разбивая это, движение от черной клавиши к следующей белой клавише составляет полшага, а затем от белой клавиши к следующей черной клавише также является полушагом.

 

Обратите внимание, что в исходной строке или отрывке ноты каждый раз на нотоносце поднимаются на один шаг вверх, а затем за нотами следует четвертная пауза. В ретроградном, где порядок изменен, сначала идет четвертная пауза, а за ней следуют три ноты в обратном порядке. Кроме того, поскольку каждая из нот в исходном утверждении каждый раз поднимается на ступень вверх, в ретроградной, каждая из нот каждый раз понижается на ступень. В инверсии четвертная пауза следует за тремя четвертными нотами, что идентично исходному утверждению. Однако каждая из нот каждый раз понижается на шаг, что противоположно исходной строке или музыкальному отрывку, где каждая из трех нот поднимается на шаг вверх. В ретроградной инверсии порядок инверсии меняется, поэтому за четвертной паузой следуют три четвертные ноты. Тем не менее, каждая из трех нот поднимается на один шаг вверх, как в исходном утверждении, но высота тона отличается.

 

Как уже упоминалось, первоначальная идея этого исследования заключалась в том, что, поскольку исходное утверждение в формальной логике и контрапозитив исходного утверждения были логически эквивалентны, исходная линия или отрывок музыки и ретроградная инверсия были бы одним и тем же отрывком музыки в некоторых способ. Однако этот простой отрывок показывает, что это не так. Было совершенно очевидно, что таблица истинности не может быть использована, чтобы показать, что исходная строка или отрывок музыки и ретроградная инверсия эквивалентны таким же образом, подобно отношениям, разделяемым исходным утверждением и контрапозитивом в формальной логике. Кроме того, таблицу истинности нельзя было использовать, чтобы показать, что ретроградность и инверсия эквивалентны таким же образом, как и обратное и обратное. Поэтому было выбрано новое направление для исследования, чтобы идентифицировать другую эквивалентность, «музыкальную эквивалентность», которую можно исследовать и определить, которая не требует таблицы истинности или формального математического доказательства, чтобы показать эквивалентность.

Определение «музыкальной эквивалентности»

В приведенном выше простом музыкальном произведении проявляются некоторые интересные характеристики, которые, возможно, приводят к определению «музыкальной эквивалентности». В этом простом примере исходная музыкальная линия или пассаж и ретроградная инверсия не совсем совпадают. За исключением первой ноты исходного отрывка и последней ноты ретроградной инверсии, ноты не совпадают. Ритмическая структура исходной строки или музыкального отрывка отличается от ретроградной инверсии, поскольку в исходном музыкальном отрывке за тремя четвертными нотами следует четвертная пауза, а в ретроградной инверсии четвертная пауза сопровождается тремя четвертными нотами. То же самое можно сказать о ретроградности, инверсии и их «музыкальной эквивалентности». Они не одинаковы. За исключением первой ноты инверсии и последней ноты ретроградности, ноты не совпадают. Кроме того, ритмическая структура инверсии отличается от ретроградной, поскольку в инверсии за тремя четвертными нотами следует четвертная пауза, а в ретроградной — четвертная пауза, за которой следуют три четвертные ноты. Из этого следует, что есть только одна характеристика, которая может способствовать понятию «музыкальной эквивалентности», и это гарантия того, что у них есть одна общая нота, которая может не находиться в одном и том же положении. На самом деле одни и те же ноты будут первой нотой в одной структуре и последней во второй структуре, когда эти две структуры «музыкально эквивалентны», и это работает только в одном направлении. Например, первая нота исходной строки или отрывка музыки и последняя нота ретроградной инверсии совпадают, но здесь нельзя добавить наоборот, поскольку эта идея работает только в одном направлении.

 

Чтобы развить или опровергнуть идею «музыкальной эквивалентности», необходимо более глубокое погружение, и это погружение заключается в фактической музыкальной структуре или паттернах высоты тона нот. Давайте рассмотрим следующие сценарии из более сложной оригинальной музыкальной линии.

• Исходная музыкальная строка или пассаж подпрыгивает на целый тон вверх, а затем еще на целый шаг вверх, а затем вниз на полтона, в то время как ретроградный пойдет вверх на полтона, а затем вниз на целый тон, а затем вниз еще целый шаг:

Original Musical Line                     Retrograde

• Исходная нотная строка или пассаж подпрыгивает на целый тон вверх, а затем еще на целый тон вверх, а затем вниз на полтона, а инверсия будет опускаться на целый тон, а затем еще на целый тон вниз, а затем обратно вверх еще на полшага:

 

      Оригинальная музыкальная линия                         Инверсия

 

• Исходная музыкальная строка или пассаж подскакивает на целый тон вверх, а затем еще на целый шаг вверх, а затем вниз на полтона, в то время как ретроградная инверсия будет идти вниз на полтона, затем на целый тон, а затем еще на один вверх весь шаг:

 

         Оригинальная музыкальная линия                               Ретроградная инверсия

 

Исходная музыкальная линия здесь немного сложнее, чем исходный простой пассаж, который был создан, поскольку движение идет вверх и вниз, и есть целые и полутоны. С исходным отрывком считалось, что закономерности высоты тона нот будут иметь решающее значение для определения понятия «музыкальной эквивалентности». Однако это не так. Мы начали со сравнения исходной музыкальной строки или отрывка и ретроградной инверсии, поскольку они подобны исходному утверждению и контрапозитиву в формальной логике, которые логически эквивалентны. В исходном простом музыкальном отрывке исходная музыкальная линия или высказывание и ретроградная инверсия имели смещение вверх на два шага, но ноты или высота звука были разными. Здесь идея движения между нотами была еще многообещающей. Однако в более поздней более сложной оригинальной музыкальной линии исходная музыкальная линия или пассаж и ретроградная инверсия имели очень разные движения. В исходной музыкальной строке или отрывке движение было на два целых шага вверх и на полшага вниз, тогда как в ретроградной инверсии ноты двигались на полшага вниз, а затем на два целых шага вверх. Один только этот пример развеивает идею о том, что паттерны высоты нот могут иметь решающее значение для определения «музыкальной эквивалентности».

Резюме и выводы

В то время как были идеи о способе определения «музыкальной эквивалентности», каждый раз контрпримеры доказывали, что эти идеи неверны. Единственным результатом было то, что первая нота одной из структур совпадает с последней нотой другой структуры, и это происходит только в одном направлении. Необходимо провести дальнейшие исследования для определения характеристик «музыкальной эквивалентности». Другой возможностью для исследования может быть разработка структуры для определения «музыкальной эквивалентности», аналогичной таблице истинности в формальной логике, которую здесь нельзя использовать. Кроме того, исследования могут выяснить, когда ноты или высота звука «музыкально эквивалентных» структур могут быть одинаковыми или когда одинаковыми являются ритмические структуры.

 

Лично я понял, что математика — это не то слово, которого следует бояться, а дисциплина, которую следует ценить больше. Я узнал, что математика есть везде, где я никогда не думал. Я заключаю также, что математика ……

 

Контакты: [email protected], [email protected]

 

---

Каталожные номера

[1] Смит, Р. Б. (1966). Серийный состав . Издательство Оксфордского университета. 1966.

 

 

Формальная логика: Символизация аргументов в сентенциальной логике – Философия на 1000 слов: Вводная антология

Автор: Томас Меткалф
Категория: Логика и рассуждение предоставить доказательства или доказать какой-либо вывод.[1] Формальная логика — это инструмент, который мы можем использовать для представления и оценки аргументов. Некоторые аргументы лучше других, и формальная логика может помочь нам понять, как именно должен работать тот или иной аргумент, и является ли он хорошим или плохим аргументом (и почему).

Чтобы использовать формальную логику, мы символизируем аргументы: мы представляем аргументы на английском (или другом естественном языке) в некотором другом наборе символов. Эти символические представления могут значительно облегчить проверку того, является ли определенный аргумент действительным (т. е. обязательно, если его посылки верны, его вывод верен), а также определить другие важные свойства аргументов.

Здесь мы рассмотрим простейшую разновидность формальной логики: сентенциальную логику. ^[2]

Розеттский камень.

1. Буквы предложений и константы

В логике высказываний, ^[3] стандартно обозначать отдельные декларативные предложения , т. е. высказывания, заглавными латинскими буквами, например:

• приносим извинения за опрокидывание мотоциклов.’
• B: « B eans полезны для сердца».
• C: «В городе c есть тысяча вещей, которые я хочу вам сказать».

Обратите внимание, что ни один из A-C не содержит слов «не», «и», «или», «если» или «тогда». Это потому, что эти слова (иногда называемые «логическими константами») очень важны в формальной логике. Мы резервируем для них специальные символы, перечисленные ниже. ^[4] Напротив, мы могли бы использовать букву «А» для обозначения «Я прошу прощения за то, что опрокинул ваши мотоциклы» в одном аргументе, и ту же букву «А» для «Счеты хуже цифрового калькулятора». в другой.

Если предложение содержит одно из этих слов «и», «не» и т. д., мы разбиваем его на составные части, разделенные этими словами. Например, если бы мое предложение было:

• Прошу прощения за то, что опрокинул ваши мотоциклы и бобы не полезны для сердца

, тогда я мог бы написать:

• A & ¬B.

Если отдельное предложение не содержит логических констант, мы можем назвать его «атомарным» предложением: его больше нельзя разделить.

Вот набор символов для констант, наряду с английскими словами, которые мы используем для приблизительного обозначения этих констант для любых предложений φ, ψ и т. д. В разных языках логики иногда используются разные символы, поэтому я включу все наиболее общие с их стандартными именами и значениями. ^[5]

Название	Символ	Альтернативные символы	Английский прибл.
‘отрицание’	¬	~ φ	‘не φ’ [6]
‘соединение’	7 a & ψ	7777777777777777777777777777777777777777777777777777 гг. φ и ψ’
«Дизъюнкция»	φ ∨ ψ		‘φ или ψ’ [7]
‘Условный’	φ → ψ	φ ⊃ ψ	‘if φ тогда ψ’ или ‘φ только если ψ’ [8]
‘biconditional’ or ‘Logical’ 70078	‘biconditional ↔ ψ	φ ≡ ψ	‘φ и только тогда, когда ψ’ (иногда написано ‘φ ψ ψ’)
‘Заключение’	∴ φ		‘Следовательно,		‘. Противоречие’	⊥		[какое-то ложное предложение] [9]
‘Entailment’	φ, ψ ⊢ χ		‘φ and ψ jointly entail χ in the system of logic in use’ [10]

As you видите, еще один важный набор символов, которые мы можем использовать, — это строчные греческие буквы. Мы используем их как переменные, а не сокращения определенных предложений: они заменяют то или иное предложение . Это предложение не обязательно должно быть атомарным; он может сам содержать логические константы.

Заглавные буквы сокращают конкретных предложений, которые мы уже определили, в то время как строчные буквы обозначают любое предложение вообще. Вот несколько примеров:

	Символизация
Я не сплю или если я слон, то огонь горяч.	¬D ∨ (E → F)
Если деньги в конверте, а в конверте нет, то верно противоречие.	(М и ¬М) → ⊥
Ворота открыты тогда и только тогда, когда: вертолет приземлился и либо лед растаял, либо вы не шутите.	G ↔ (H & (I ∨ ¬J))

Мы также можем использовать круглые скобки, чтобы упростить чтение наших предложений и сделать их понятными. Например, во втором предложении чуть выше, если бы я расставил скобки по-другому, значение изменилось бы:

Ворота открыты тогда и только тогда, когда вертолет приземлился. И то ли лед растаял, то ли вы не шутите.

(G ↔ H) & (I ∨ ¬J)

2. Доказательства

Обратите внимание, что мы использовали английские слова для аппроксимации наших символов. Это не случайно. Например, в сентенциальной логике, если вы знаете, что А истинно, и вы знаете, что Б истинно, вы можете заключить, что «А и В» истинны. И именно так мы используем наше английское слово «и». У вас не может быть и Acura , и линкора, если это правда, что у вас есть Acura и это правда что у вас линкор.

Обратите внимание, что если вы знаете, что у вас есть Acura и линкор, вы можете сделать вывод, что у вас есть Acura. Чтобы символизировать это, мы бы сказали, что если вы знаете «А и В», вы можете заключить «А». Можно считать, что если у вас Акура, то у вас есть машина. Мы могли бы символизировать это с помощью «A → C». В свою очередь, мы можем, , предполагая , что у вас есть Acura и линкор, докажите , что у вас есть машина. Это может выглядеть так:

Число	Предложение	Обоснование
1.	А и Б	Предположение.
2.	А → С	Успение.
3.	A	Следует из 1.
4.	∴ C	Следует из 2 и 3.

Как видите, мы идем шаг за шагом, нумеруя наши шаги и указывая, как мы получили наше новое предложение.

Это всего лишь быстрый пример, но вы, вероятно, можете себе представить, как мы можем использовать эти символы для построения более интересных доказательств. Тема доказательств вообще достаточно важна и сложна, чтобы иметь отдельную запись.

3. Помимо сентенциальной логики

Когда мы знаем правила сентенциальной логики и логические константы, несложно символизировать более сложные предложения. Например, мы можем захотеть поговорить о том, какие объекты обладают какими свойствами, или о том, является ли некоторое предложение обязательно истинным или вероятно истинным. Но это темы для других статей.

Примечания

^[1] В этом эссе мы не говорим явно ни о дедукции, ни о индукции, потому что в обоих случаях можно использовать сентенциальную логику. Однако сентенциальная логика обычно вводится дедуктивными аргументами.

^[2] Здесь мы следуем стандартному способу обозначения аргументов. См., например, Huber 2019 и Sider 2010.

^[3] Иногда это называют «пропозициональной» логикой. Но «сентенциал» более нейтрален. Он лишь обязывает нас к существованию предложений, т. е. грамматических цепочек слов в некотором языке. Это не обязывает нас к существованию пропозиций, которые, если они существуют, являются (грубо говоря) значениями предложений, или содержанием мысли, или тем, что «это» является «истинным», когда я говорю: «Это верно, что электроны меньше, чем протоны.» Сказать «сентенциальный» также, строго говоря, более точно: то, что мы в основном делаем в формальной логике, является синтаксическим, а не семантическим. То есть мы рассматриваем строки из символов , а не значений, стоящих за символами, а пропозиции (если они существуют) являются значениями предложений.

^[4] Мы называем специальные символы «логическими константами», потому что, в отличие от букв-предложений, они всегда означают одно и то же, где бы они ни встречались.

^[5] Есть несколько других английских слов или терминов, которые также соответствуют этим символам. Например, строка «p, только если q» оказывается эквивалентной «если p, то q». И в стандартной логике «но» и «и» подчиняются одним и тем же правилам; мы не упоминаем коннотацию контраста, присущую «но».

^[6] Конечно, в английском языке мы обычно не говорим о том, является ли «не р» истинным или ложным; мы говорим о том, является ли «не [некоторое предложение]» истинным или ложным. То есть мы не упоминаем саму букву «р»; мы заполняем его любым предложением, о котором говорим. Чтобы упомянуть фразу, содержащую переменную, но указать, что вы собираетесь упомянуть значение переменной, а не имя самой переменной, вы можете использовать угловые кавычки (т. е. ‘⌜’ и ‘⌝’) для того, что иногда называют «квазицитированием» (Quine 1981 [1940]: 33-37). Однако, чтобы избежать путаницы, я решил сохранить одинарные кавычки.

^[7] Обратите внимание, что в английском языке наше слово «или» может означать включающее или исключающее «или», то есть иногда мы используем «или», чтобы подразумевать, что одно или оба могут быть истинными, в то время как мы иногда используйте его, чтобы подразумевать, что только одно может быть правдой. Например, если я спрашиваю: «Вы когда-нибудь ездили на скутере или мотоцикле?», я, вероятно, повышаю голос в конце предложения, подразумевая, что ответ «да» или «нет», и вы бы скажите «да», если вы ездили на одном из них, но также, если вы когда-то ездили на обоих. Но если я спрошу «Хочешь суп или салат?» в ресторане, я могу понизить голос в конце предложения, подразумевая, что вы должны выбрать, а «и то, и другое» — не вариант. В стандартной логике наш символ дизъюнкции означает включающее «или», то есть он оказывается истинным, даже если оба p и q истинны. Если мы хотим указать исключающее или, мы можем использовать символ отрицания. Например: ‘(A ∨ B) & ¬(A & B)’

^[8] Это приближение может быть особенно запутанным. Строго говоря, «условные» символы (иногда называемые также «материальными условными» символами) в стандартной логике говорят, что ложно, что: p истинно, а не-q истинно . В реальной жизни мы почти всегда можем прочитать это как «если p, то q», но бывают и несколько запутанные случаи. О них мы еще поговорим в записях о таблицах истинности. Но на данный момент, в стандартной сентенциальной логике, условное утверждение будет считаться истинным всякий раз, когда антецедент (часть «если») ложна, и всякий раз, когда антецедент и следствие (часть «тогда») оба истинны. Как я уже сказал, это может немного сбивать с толку.

^[9] Символ обычно используется для обозначения противоречия, но для целей доказательства обычно достаточно, чтобы предложение было ложным. Мы вернемся к этой теме, когда будем рассматривать фактические доказательства.

^[10] Последняя строка в таблице не об истинности предложений, а о выводимости в нашей системе логики. Это может сбивать с толку, пока мы не узнаем о фактических доказательствах, использующих эти символы, так что не беспокойтесь об этом слишком сильно, но я хотел включить их для полноты картины. По сути, он говорит, что если у вас есть p в строке и у вас есть q в строке, вы можете добраться до r, используя правила логики.

Ссылки

Хубер, Франц. 2019. Логическое введение в теорию вероятности и индукции . Нью-Йорк, штат Нью-Йорк, и Оксфорд, Великобритания: Издательство Оксфордского университета.

Куайн, В. В. 1981 [1940]. Математическая логика , исправленное издание. Кембридж, Массачусетс: Издательство Гарвардского университета.

Сайдер, Тед. 2010. Логика для философии . Нью-Йорк, штат Нью-Йорк, и Оксфорд, Великобритания: Издательство Оксфордского университета.

Благодарности

Автор выражает благодарность редакции 1000-Word Philosophy , а также Майклу Ферри, Эндрю Лавину и Дэниелу Мэсси за полезные комментарии к этому эссе.