Первые уроки по изучению площади, страница 2
Математика \ Методика обучения математике в начальной школе
Учитель последовательно организует работу с каждой фигурой.
Найдите на листе фигуру под номером 1. Покройте ее квадратными сантиметрами.
Рис.4.
Сколько квадратных сантиметров в фигуре 1? (3.) В этом случае говорят, что площадь фигуры 1 равна трем квадратным сантиметрам. Объясните, что значит, что площадь фигуры 1 равна трем квадратным сантиметрам. (Это значит, что в фигуре 1 содержится 3 квадратных сантиметра.) Что такое квадратный сантиметр? (Это квадрат со стороной 1 см.) На листе под фигурой 1 учащиеся делают соответствующую запись: 3 кв. см.
С
помощью моделей квадратных сантиметров учащиеся измеряют также площадь фигуры
2 и результат записывают под ней. После выполнения этой работы учитель говорит,
что ,так измерять площадь долго и трудно. Легче разбить фигуру на квадратные
сантиметры с помощью линейки и карандаша и затем подсчитать их число.
Проверяя правильность выполнения задания, учитель не только просит назвать величину площади, но и спрашивает, что значит, что площадь фигуры равна, например, 14 кв см. (Это значит, что в фигуре содержится 14 квадратных сантиметров, т. е. 14 квадратов со стороной 1 см.)
Следующий
этап — знакомство с палеткой и измерение площади с помощью палетки. Это может
быть сделано в процессе такой беседы. Расчерчивать фигуру на квадратные
сантиметры, говорит учитель, тоже довольно трудно. Для того чтобы облегчить
задачу определения площади фигур, применяется прозрачная пленка, разделенная на
квадратные сантиметры (палетка). Для нахождения площади фигуры достаточно
наложить палетку на фигуру так, чтобы стороны квадратов на палетке совпали со
сторонами фигуры. (Для демонстрации очень удобно использовать кодоскоп.) После
показа палетки и измерения посредством ее площади фигуры учитель дает задание:
измерить площади фигур 4 и 5, используя палетку.
Так как фигура 5 — прямоугольник, то при проверке задания проводится дополнительная работа, целью которой является подготовка к выводу правила вычисления площади прямоугольника. Учащиеся под руководством учителя находят два рациональных способа подсчета числа квадратов, содержащихся в прямоугольнике. Можно также предложить учащимся измерить длину и ширину прямоугольника и сравнить полученные числа с числом квадратных сантиметров в ряду и количеством рядов, с числом квадратных сантиметров в столбце и количеством столбцов. Здесь же проводится работа по предотвращению смешения учащимися понятии площадь прямоугольника и периметр прямоугольника.
Дается
задание: определить периметр прямоугольника 5. Ставится ряд вопросов: что
нужно сделать, чтобы найти площадь прямоугольника? (Нужно разбить его на
квадратные сантиметры и подсчитать их число.) Что нужно сделать, чтобы найти
периметр прямоугольника? (Нужно измерить его стороны и найти сумму длин всех
сторон. ) В каких единицах измеряется площадь? (В квадратных сантиметрах) . В
каких единицах измеряется периметр? (В сантиметрах).
) В каких единицах измеряется площадь? (В квадратных сантиметрах) . В
каких единицах измеряется периметр? (В сантиметрах).
Для закрепления нового материала выполняются упражнения 382 и 383. При подведении итога урока учитель еще раз подчеркивает все основные положения рассмотренного на уроке материала.
Вывод правила о вычислении площади прямоугольника проводится так, как это описано в методических пособиях и в учебнике с небольшими, но очень важными, на наш взгляд, дополнениями. Вычисляя площадь прямоугольника по правилу, необходимо подчеркивать, что, находя произведение чисел — значений длины и ширины прямоугольника, — мы фактически подсчитываем число квадратных сантиметров, содержащихся в нем. На первых уроках, а при затруднениях и на последующих, мы считаем необходимым требовать от учащихся словесного обоснования необходимости выполнения действия умножения над соответствующими числами для определения площади прямоугольника.
Это
обоснование может выразиться в виде таких рассуждений.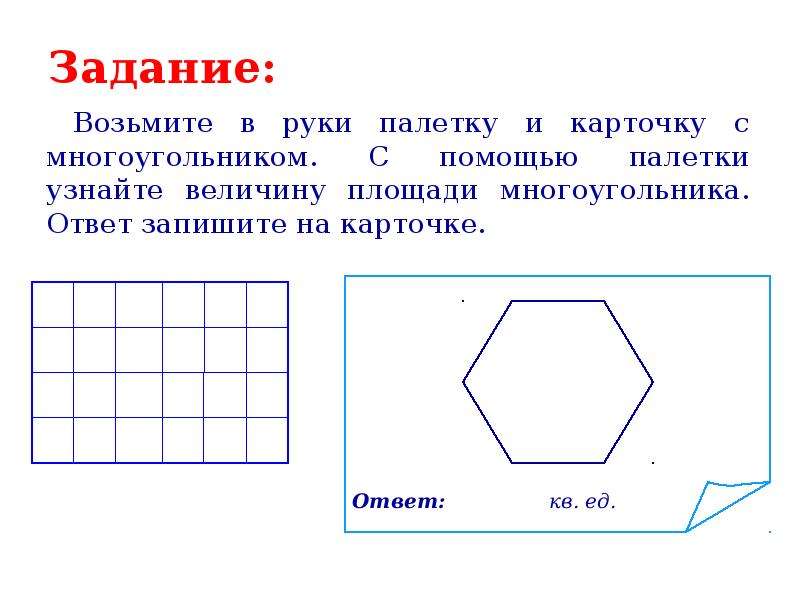
Нам нужно, найти площадь в квадратных сантиметрах прямоугольника, длина которого равна 5 см, а ширина 4 см. Найти площадь прямоугольника — значит определить число квадратных сантиметров, помещающихся в нем. Длина данного прямоугольника 5 см, значит, по его длине в одном ряду (полосе) уложится 5 квадратных сантиметров. Так как ширина прямоугольника 4 см, то таких рядов (полос) в нем будет 4, т. е. в прямоугольнике содержится 4 ряда по 5 квадратных сантиметров в каждом ряду. Тогда весь прямоугольник содержит 5*4 кв. см, или 20 кв. см. Площадь прямоугольника равна 20 кв. см. Аналогичные рассуждения проводятся и для другого способа подсчета числа квадратов.
Не приводя здесь подробно хода урока по ознакомлению со способом вычисления площади прямоугольника, отметим лишь последовательность формирования навыка вычисления площади прямоугольника.
Определение площадей прямоугольников, длина одной из сторон которых равна 1 см.
Определение
площадей -прямоугольников, длины сторон которых более 1 см и выражаются
натуральными числами, путем разбиения их на квадратные сантиметры одним из
способов, затем путем разбиения на полосы или столбцы шириной в 1 см и,
наконец, с помощью нанесения только делений по длине и ширину.
Формулировка правила. Вычисление площади прямоугольника путем нахождения произведения соответствующих чисел с обоснованием и последующей проверкой результата путем разбиения прямоугольника на квадратные сантиметры палеткой или расчерчивания и непосредственного их подсчета.
Выработка умения вычислять площадь прямоугольника по его длине к ширине. Обоснование и непосредственное измерение требуется от учащихся лишь в случае затруднения или при обнаружении ошибки.
Первый, второй и третий этапы в основном выполняются на одном уроке. Четвертый этап продолжается в течение всех последующих уроков до полного и осознанного овладения учащимися соответствующим умением.
Представленная здесь последовательность формирования умения вычислять площадь прямоугольника позволяет добиться прочности и осознанности его усвоения. Учащиеся получают возможность проводить самоконтроль при выполнения заданий на определение площади прямоугольника.
Яркие,
конкретные представления о смысле измерения площади, которые учащиеся получают
в процессе выполнения приведенных в статье упражнений, и выполнение в дальнейшем
заданий на определение площади и периметра одного я того же прямоугольника предупреждают
смещение понятий площадь прямоугольника и периметр прямоугольника.
Использование палетки на первых этапах ознакомления с площадью позволяет подчеркнуть общность понятия площади для всех фигур независимо от их формы. На уроке же, который посвящен измерению площади палеткой (№ 397—399), учитель знакомит учащихся с приближенным вычислением площади фигур, показывает целесообразность применения для этого палетки. При этом в задания по определению приближенных значений площади можно включать также и прямоугольники, длины сторон которых не содержат целое число сантиметров.
Рассмотренный
подход к изучению площади исключает возможность ошибочного толкования
различных способов измерения площади. Учащиеся при необходимости могут
обосновать определение площади прямоугольника через произведение
соответствующих чисел, опираясь на общие представления о смысле измерения
площади. Умение проводить такое обоснование позволяет контролировать себя при
выполнении заданий, требующих нахождения площади прямоугольника и его периметра.
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им.
 Сухого 4467
Сухого 4467 - ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Методика изучения темы «площадь».
Методика формирования представлений о пощади фигуры строится в соответствии с общей методикой формирования представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное — большее или меньше — место на плоскости.
I этап — ознакомление учащихся с термином «площадь».
Для разъяснения этого понятия использую демонстрационные или
индивидуальные модели различных фигур.
На доске фигуры:
2
Вопросы:
-Какая из этих фигур занимает больше
места на доске? ( 5 ) Говорят, что фигура
5 имеет большую площадь, чем фигура 1, 2,
3, 4.
Учитель показывает эти фигуры, путем
наложения их друг на друга учащиеся
устанавливают, что площади 1-ой и 2-ой
фигур одинаковы, а площадь 4-ой меньше
площади 5-ой, т.к. вся 4-ая фигура
помещается внутри 5-ой, и т.д. Учитель
предлагает выписать номера фигур,
расположив их в порядке возрастания
площадей. Проверяя, как учащиеся
усвоили новый термин, учитель показывает
еще пару моделей фигур и спрашивает:
«Как узнать, площадь, какой фигуры
больше?» (Нужно наложить одну фигуру
на другую.) Учитель просит одного
из учеников продемонстрировать это. Ставятся вопросы: «Площадь, какой
фигуры больше?», «Площадь какой
фигуры меньше?». После выполнения
этого задания целесообразно провести
практическую работу с раздаточным
материалом. Каждому ученики дается по
две фигуры (№1 и №2) — могут быть у всех
различными. Важно лишь, чтобы одна из
них полностью помещалась в другой. Для
быстроты проверки результатов
сравнения можно пронумеровать фигуры
так, чтобы в каждой паре цифрой 1 была
обозначена фигура с большей площадью.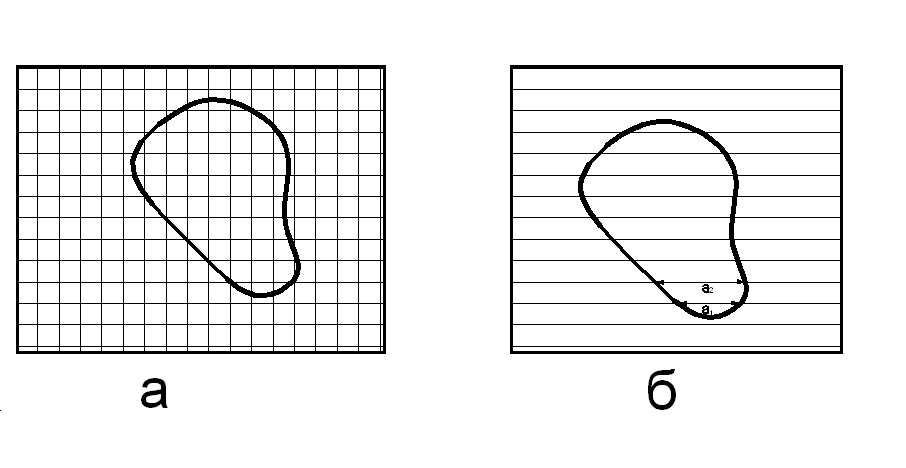 Учащимся дается задание: сравнить
площади данных им фигур и выписать (или
назвать) их номера в порядке возрастания
площади. Для записи ответов удобно
использовать индивидуальные доски.
Во время выполнения работы он наблюдает,
как дети проводят сравнение. Затем
учитель может провести фронтальную
работу с классом. Он предлагает сравнить
на глаз, а тем путем наложения площади
двух таких фигур, по отношению к которым
вопрос не может быть решен тем же способом
(имеется в виду наложение).
Учащимся дается задание: сравнить
площади данных им фигур и выписать (или
назвать) их номера в порядке возрастания
площади. Для записи ответов удобно
использовать индивидуальные доски.
Во время выполнения работы он наблюдает,
как дети проводят сравнение. Затем
учитель может провести фронтальную
работу с классом. Он предлагает сравнить
на глаз, а тем путем наложения площади
двух таких фигур, по отношению к которым
вопрос не может быть решен тем же способом
(имеется в виду наложение).
Рис.1
С обратной стороны эти фигуры разбиты на одинаковые квадраты. Возникает проблемная ситуация. Учащиеся говорят, что путем наложения нельзя определить, площадь какой фигуры больше. Тогда учитель поворачивает фигуры обратной стороной. Учащиеся при этом обычно сами догадываются, как можно сравнить данные фигуры по площади (квадраты нужно посчитать).
Формулируется вывод: если фигуры
нельзя сравнить по площади наложением,
то можно каждую из фигур разбить на
одинаковые между собой фигуры (квадраты)
и затем подсчитать «сколько их содержится
в каждой фигуре.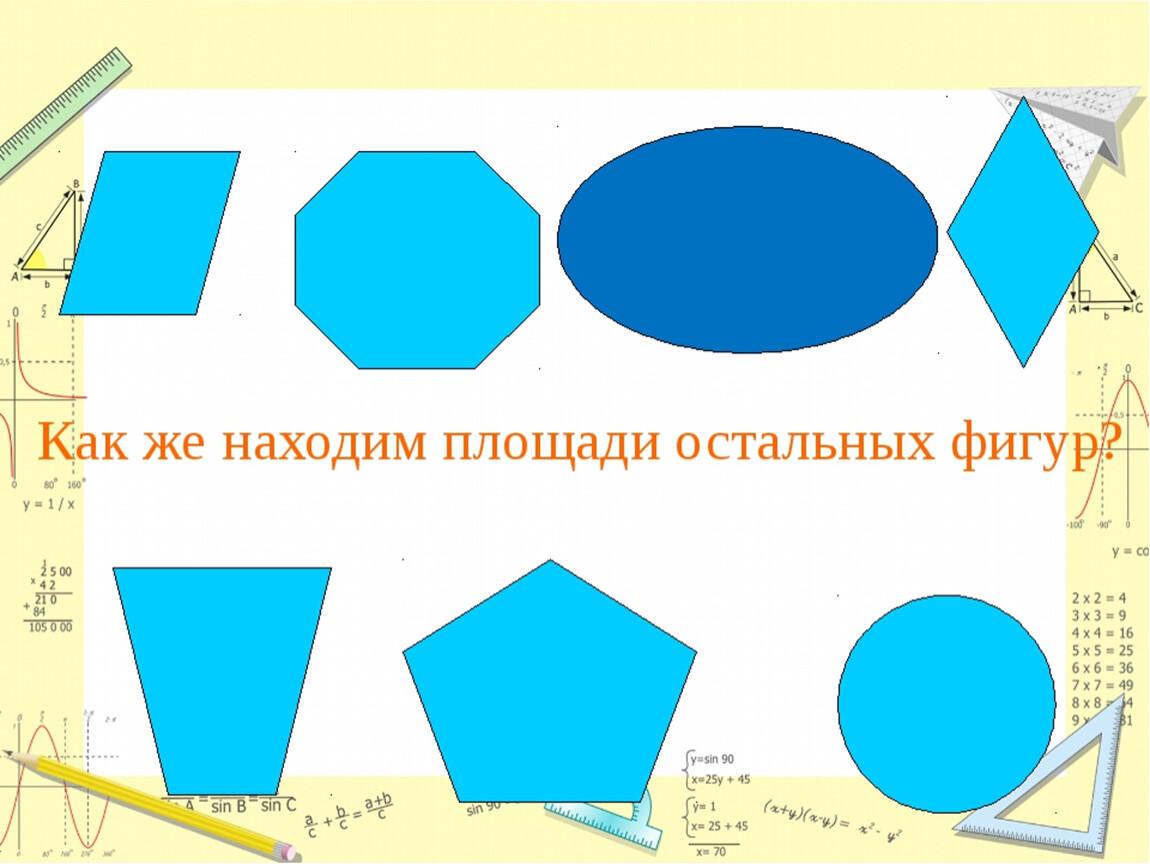 Фигура, в которой
содержится большее число таких одинаковых
фигур, имеет большую площадь.
Фигура, в которой
содержится большее число таких одинаковых
фигур, имеет большую площадь.
Для закрепления: учитель показывает две фигуры, разбитые так, ………………………………………………………………………………
Рис.2
Дети приходят к выводу, что при таком разбиении сравнить площади фигур путем подсчета числа квадратов нельзя. (! Ни в коем случае не должен прозвучать ответ, что эти фигуры вообще нельзя сравнить по площади.)
Обратную сторону этих фигур можно разбить на одинаковые между собой фигуры и затем их сравнить.
Следует обратить внимание учащихся на тот факт, что при сравнении площадей необходимо пользоваться одной, и той же меркой.
П этап — знакомство с квадратным сантиметром.
На втором уроке учащиеся знакомятся с
единицей площади — квадратным сантиметром,
учат измерять площади фигур путем
разбиения их на квадратные сантиметры
с помощью линейки и карандаша, путем
наложения кв. сантиметра на фигуры. К
уроку готовится раздаточный материал:
модели квадратных сантиметров, листы
нелинованной бумаги с изображениями
геометрических фигур. После введения
кв.сантиметра учащимся предлагается
начертить в тетради квадратный сантиметр
и написать 1 см². затем они находят
кв.сантиметр у себя на партах, после
чего проводят практическую работу по
измерению площади.
сантиметра на фигуры. К
уроку готовится раздаточный материал:
модели квадратных сантиметров, листы
нелинованной бумаги с изображениями
геометрических фигур. После введения
кв.сантиметра учащимся предлагается
начертить в тетради квадратный сантиметр
и написать 1 см². затем они находят
кв.сантиметр у себя на партах, после
чего проводят практическую работу по
измерению площади.
С одержание листов у всех одинаково и может быть таким. Учитель последовательно организует работу с каждой фигурой: найдите на листе фигуру под №1. Покройте ее квадратным сантиметром (или сантиметрами).
Р ис. 3.
1 2 3 4 5
Сколько кв.см в фигуре №1 ? В этом случае
говорят, что площадь фигуры 1 равна трем
квадратным сантиметрам. Объясните, что
значит, что площадь фигуры 1 равна
трем квадратным сантиметрам. (Это
значит, что в фигуре I содержится три
кв.см.) Что такое квадратный сантиметр?
(Это квадрат со стороной I см) На
листе под фигурой 1 учащиеся делают
соответствующую запись: 3 см².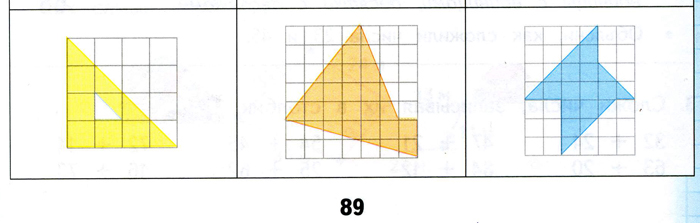
ІП этап – вычисление площади.
Вывод правила о вычислении площади прямоугольника проводится так: учитель предлагает ученикам начертить в тетрадях прямоугольник длиной 7 см и шириной 3 см, разделить его на квадратные сантиметры и подсчитать, сколько кв .см получилось. Учитель чертит на доске прямоугольник, длины сторон которого 7 дм и 3 дм.
Беседа.
1. Разделим противоположные стороны прямоугольника так, чтобы каждое деление было равно одному сантиметру. Соединим отрезками точки деления, которые расположены на противоположных сторонах фигуры.
Сколько полос получилось? (3 полосы, каждая длиной 7 см)
2. Соединим отрезками точки, расположенные на двух других противоположных сторонах.
3. Сколько всего квадратов в прямоугольнике?
(21 квадрат — 7 на 3) Значит, если длину
прямоугольника умножить на его ширину,
то получится число, которое покажет,
сколько квадратов в прямоугольнике.
4. А как еще можно подсчитать квадраты? (Можно по 3 квадрата взять 7 раз, получится 21 квадрат.)
После этого учитель предлагает ученикам прочитать правило вычисления площади прямоугольника.
3 кл. (1-3) № 445.
ІV этап — знакомство с кв. дециметром Стр. 143 (1-3)
В тетрадях чертят квадрат со стороной I дм. Затем вычисляется площадь начерченного квадрата в квадратных сантиметрах, устанавливается, что 1 дм²=100 см².
Учащиеся вычисляют площадь доски в квадратных сантиметрах — это получится довольно большое число. Поэтому выгодно применить новую единицу измерения площади — кв.дм. Под руководством учителя выполняются упражнения:
1. Сколько кв.см содержится в 2 дм², 5 дм²?
2. Сколько кв.дм составляют 300 см², 600 см² ? .
Vэтап — знакомство с квадратным
метром, кв. мм, кв. км
мм, кв. км
На уроке цесообразно показать бумажную модель квадратного метра. Или продемонстрировать соответствующие кадры диафильма. Разделить стороны на дециметры, соединить эти точки, подсчитать, сколько кв.дм в кв.м:
I м² = 100 дм².
А один кв.дм разделить на кв.см и получим:
I дм² = 100 см².
Значит,
1м²= 10000 см².
На последующих занятиях учащиеся решают задачи на вычисление площадей, также решают обратные задачи на нахождение одной из сторон по известной площади и другой стороне прямоугольника, преобразование различных единиц площади: более крупные в более мелкие и наоборот.
VІэтап
По программе «1-4″ в 4 кл. знакомятся с кв.мм и его соотношения. По программе»1-3» — этого не изучают.
Га и ар.
VП этап — знакомство
с палеткой.
Это может быть сделано в процессе такой беседы:
— Расчерчивать фигуру на квадратные сантиметры, — говорит учитель, — тоже довольно трудно. Для того, чтобы облегчить задачу определения площади фигур, применяется прозрачная пленка, разделенная на кв.см (палетка). Для нахождения площади фигуры достаточно наложить палетку на фигуру так, чтобы стороны квадратов на палетке совпадали со сторонами фигуры. После показа палетки и измерения посредством ее площади фигуры, учитель дает задание: измерить площади фигур, используя палетку. Учитель следит за тем, чтобы учащиеся правильно накладывали палетку на фигуру.
В № 437 (по 1-3) объяснено, как надо применять палетку. На фигуру накладывают палетку. Для этого подсчитают, сколько кв.см уложилось внутри фигуры. Полных кв.см — II. Неполных кв.см — 16. 16 неполных — это приблизительно 8 полных кв.см. Площадь всей фигуры ІІ+8=19(см²).
Как посчитать площадь слоя в сантиметрах с помощью фотошопа
спросил
Изменено 9 лет, 1 месяц назад
Просмотрено 7к раз
Я хочу рассчитать размер области слоя в сантиметрах с помощью фотошопа. Есть ли какой-нибудь инструмент для этого, кроме линейки? Слой, который мне нужен для вычисления размера его площади, не имеет правильной формы.
Есть ли какой-нибудь инструмент для этого, кроме линейки? Слой, который мне нужен для вычисления размера его площади, не имеет правильной формы.
Я задал свой вопрос в stackoverflow и получил такой ответ:
https://stackoverflow.com/questions/7613789/how-to-calculate-the-area-of-a-layer-in-centimeters-using-photoshop
Информационная страница в фотошопе показывает максимальную высоту и ширину выбранного слоя. поэтому, когда мой слой имеет случайную форму, эти числа не могут помочь мне рассчитать размер области.
У меня недостаточно репутации для загрузки изображения, поэтому откройте ссылку выше.
- Adobe-Photoshop
Было бы замечательно иметь возможность делать это автоматически, скажем, с помощью инструмента лассо, отображающего это свойство, но я не смог найти графическую программу, которая выводит эти данные.
Что мне пришлось сделать, так это вручную ввести координаты X, Y, если вершины многоугольника в электронную таблицу Excel, и использовать их для расчета площади в пикселях. Излишне говорить, что это утомительный процесс.
Излишне говорить, что это утомительный процесс.
Будем рады любым другим предложениям.
теги поиска:- Как вычислить площадь неправильного многоугольника на изображении. Как найти площадь неправильного многоугольника на изображении.
Два программных решения:
- CellProfiler
- GemIdent
Вы должны использовать линейку и проверить информационную палитру — она покажет вам значение.
Щелкните значок «+». Он покажет вам некоторые параметры, а затем выберите «Сантиметры».
Используйте окно гистограммы в Photoshop (нажмите «расширенный вид»). В левом нижнем углу вы найдете количество пикселей вашего выбора. Посмотрите на это изображение для справки:
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и парольОпубликовать как гость
Электронная почтаТребуется, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

 Сухого 4467
Сухого 4467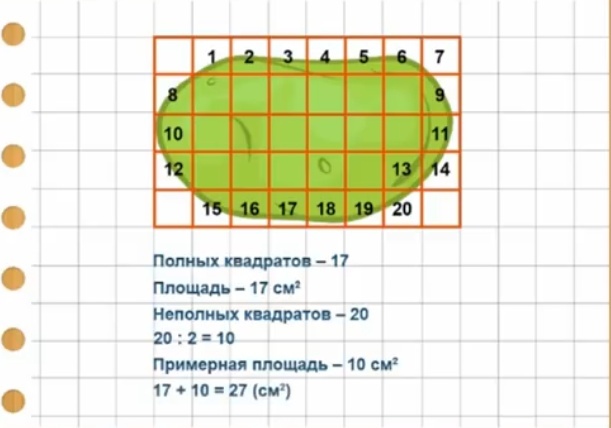 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114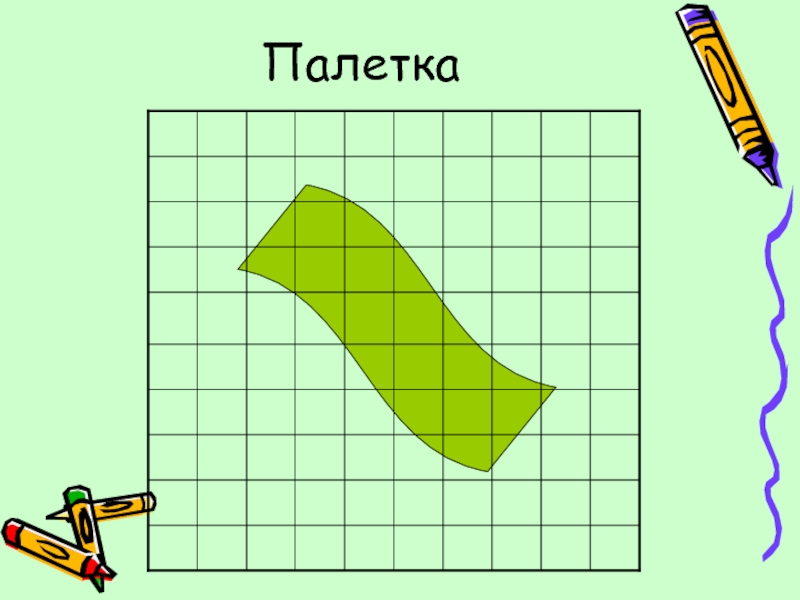 Каразина 305
Каразина 305