какой буквой или знаком пишется параметр площади в математике
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Оглавление
- Общие сведения
- Варианты обозначения
- Полезное видео
- Подведем итоги
Общие сведения
Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.
Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.
Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:
- Положительная.
В числе ее характеристик отсутствует понятие отрицательного значения. - Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
- Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
- Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
- Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.
В числе ее характеристик отсутствует понятие отрицательного значения.Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.
Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника.
Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, — возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения
Понятие используется не только в математике. Оно актуально и для физики.
В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.
Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.
Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов.
В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Более подробную информацию по математическим нюансам можно посмотреть тут.
Как обозначается площадь: какой буквой или знаком пишется параметр площади в математике
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе.
В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Содержание
Общие сведения
Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.
Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.
Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:
- Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.
- Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
- Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
- Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
- Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.
Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.
Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики.
При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения
Понятие используется не только в математике. Оно актуально и для физики.
В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину. Проститутки в Екатеринбурге intim66.ru
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.
Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.
Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами.
В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Что такое площадь в математике?
Автор:
Малкольм МакКинси
Проверено
015В геометрии площадь — это пространство плоской формы, например, многоугольника. , круг или эллипс, занимает плоскость. Площадь фигуры всегда измеряется в квадратных единицах.
Как только вы узнаете, как квадратные единицы соотносятся с площадью, вы сможете найти площадь практически любой двумерной фигуры.
Как найти площадь фигуры
Плоские фигуры имеют два измерения:
Ширина
Длина
Квадрат, например, имеет ширину равна его длине, так как длины всех сторон одинаковый.
Эллипс также имеет ширину и длину.
Мы можем легко увидеть, как квадрат можно разделить на маленькие квадратные единицы, как на координатной плоскости. Вы не можете легко увидеть, как эллипс может быть составлен из маленьких квадратов, но это возможно.
Поскольку он имеет ширину и длину, он покрывает пространство, и это пространство, даже с изогнутыми сторонами эллипса, может быть разделено на квадратные единицы:
Подсчет площади квадрата и прямоугольникаПодсчет квадратных единиц в квадрат легко: один, два, три и т. д. .
Но как посчитать все квадраты эллипса? Как определить, какая часть квадрата находится под верхней кривой? Как насчет кривых на левом и правом концах?
К счастью, у математиков есть быстрый способ сложить все квадратные единицы, не считая их. 9{2}mi2
Находите ли вы площадь четырехугольника, такого как трапеция и ромб, или любой другой замкнутой фигуры, площадь всегда будет возведена в квадрат.
Формула площади
Формула площади, которую вы используете, зависит от того, для какой фигуры вы пытаетесь найти площадь.
Площадь квадратов и прямоугольников
Чтобы найти площадь простых фигур, таких как квадрат или площадь прямоугольника, вам нужна только ширина w и длина l (или база, b ). Площадь равна длине, умноженной на ширину:
Площадь всегда возводится в квадрат. Вы всегда будете выражать площадь в квадратных единицах, полученных из линейных единиц.
Вот прямоугольник 90 метров в ширину и 120 метров в длину (самый большой размер футбольного поля ФИФА). Чему равна площадь этого прямоугольника?
Пример площади прямоугольникаПоскольку футбольное поле измеряется в погонных метрах, его площадь равна квадратным метрам. Площадь прямоугольника 10 800 метров в квадрате .
Формула площади квадрата на самом деле даже проще, чем запись длина × ширина , потому что все стороны равны:
Вот квадрат со сторонами 15 дюймов в длину, такой же размер, как основания на бейсбольном мяче MLB поле.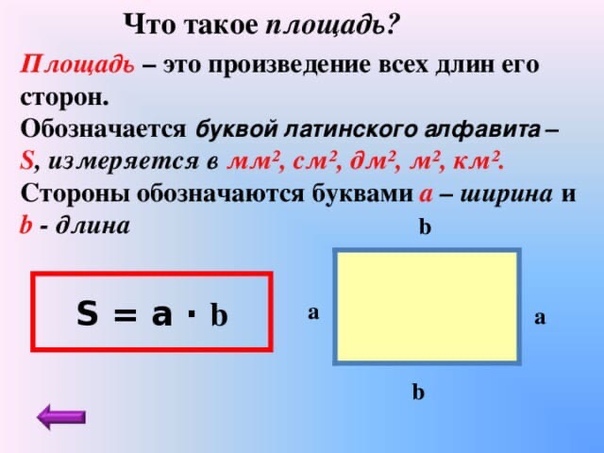
Вычисление площади для этого квадрата выглядит следующим образом:
Площадь других фигур
Все остальные многоугольники нелегко разделить на квадратные единицы. Взгляните на параллелограмм.
Две стороны пересекают многие квадратные единицы. Конечно, параллелограмм — это просто опрокинутый прямоугольник.
Итак, математически, если бы мы могли отрезать один конец и присоединить его к другому, мы бы получили площадь в квадратных единицах. Мы можем сделать именно это, поскольку площадь параллелограмма с основанием b и шириной или высотой h находится по следующей формуле:
Это та же формула, что и для квадрата. или прямоугольник!
Если разделить параллелограмм по диагонали, что получится? Два треугольника. Это означает, что площадь любого треугольника равна половине площади параллелограмма с такой же длиной основания и высотой. Помните, что параллелограмм использует ту же формулу, что и прямоугольник.
Площадь треугольника равна половине основания, b , умноженной на высоту, h :
Вот прямоугольный треугольник, парус из 45-футовый парусник Morgan с базой 201420\frac{1}{4}2041 футов и высотой 441244\frac{1}{2}4421 футов. Какова его площадь?
Пример площади треугольникаДля удобства умножения можно изменить дроби на десятичные:
Площадь треугольного паруса приблизительно равна 450,6 квадратных футов .
Как насчет домашней пластины бейсбольного поля Главной лиги бейсбола? Мы можем вычислить площадь домашней пластины пятиугольника , рассматривая его как две формы:
Прямоугольник 17 дюймов × 8,5 дюймов 90 003
9{2}216,5 дюймов2 Пример площади пятиугольника — домашняя плита- Формула геометрической площади
- Площадь треугольника
- Мы часто запоминаем формулы для вычисления площади фигур. Более простым методом было бы использование линий сетки, чтобы понять, как была получена формула.
- Мы часто путаем площадь и периметр фигуры. Полное понимание может быть построено путем отслеживания поверхности любой формы и наблюдения за тем, что область — это, по сути, пространство или область, покрытая формой.
Пример 1: Найдите площадь квадрата со стороной 7 см.
Решение :
Площадь квадрата = сторона × сторона. Здесь сторона = 7 см
Подставляя значения, 7 × 7 = 49.
Следовательно, площадь квадрата = 49 квадратных см.
Пример 2: Размеры прямоугольника 15 см и 8 см.
Найдите его площадь. Решение :
Площадь прямоугольника равна произведению его длины на ширину, что можно представить по формуле: Площадь = l × w.
Подставляя данные значения, получаем площадь прямоугольника = 15 × 8 = 120 см 2Пример 3: Можете ли вы найти площадь круга с радиусом 14 см?
Решение :
Радиус окружности = 14 см
Площадь круга рассчитывается по формуле π r 2
Подставляя значения в формулу, площадь = \(\dfrac{22}{7}\) × 14 × 14 = 616 квадратных см.
Пример 4: Вычислите площадь заданной формы путем подсчета квадратов.
Решение: Давайте посчитаем полные квадраты и половинки квадратов.
Есть 24 единичных квадрата и 5 половинных квадратов.
Следовательно, площадь фигуры = 24 + (5 × ½) = 24 + 2,5 26,5 квадратных единиц
Найдите площадь круга
Некоторые двумерные фигуры даже не являются многоугольниками, например наш эллипс или окружность.
Площадь круга с радиусом ( r ) находится по следующей формуле:
Если у вас есть круг с радиусом 4 см , вы можете легко вычислить площадь круга по формуле вверху:
Площадь круга составляет приблизительно 50,24 квадратных сантиметра.
Найти площадь эллипса
Площадь эллипса находится с использованием двух его осей: большая ось (длина от центра), обычно обозначаемая как аа, и малая ось (ширина от центра), обычно обозначаемая как bb, с помощью этой формулы:
Площадь круга и эллипсаНезависимо от того, имеете ли вы дело с правильным многоугольником или неправильной плоской фигурой, вы можете найти площадь!
Что такое площадь? Определение, площадь фигур Формула
Площадь – это площадь, занимаемая двухмерной фигурой. Другими словами, это величина, измеряющая количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартной единицей площади являются квадратные единицы, которые обычно представляются как квадратные дюймы, квадратные футы и т.
д. Давайте научимся вычислять площадь различных геометрических фигур с помощью примеров и практических вопросов.
| 1. | Что такое площадь? |
| 2. | Как рассчитать площадь? |
| 3. | Площадь геометрических фигур — Формула |
| 4. | Часто задаваемые вопросы по Зоне |
Что такое площадь?
Слово «площадь» означает свободную поверхность. Площадь фигуры вычисляется с помощью ее длины и ширины. Длина одномерна и измеряется в таких единицах, как футы (футы), ярды (ярды), дюймы (дюймы) и т. д. Однако площадь формы является двумерной величиной. Следовательно, он измеряется в квадратных единицах, таких как квадратные дюймы или (в 
Длина и ширина этих ребер учитываются при расчете площади конкретной формы.
Как рассчитать площадь?
Давайте посмотрим, как вычислить площадь фигуры с помощью сетки. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 на 1 единицу. Площадь каждого из этих квадратов равна 1 квадратной единице. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь фигуры, начерченной на сетке.
Площадь этой фигуры равна количеству заштрихованных единичных квадратов.
Таким образом, площадь фигуры = 9 квадратных единиц. Теперь давайте посмотрим на другой пример. Когда фигура не занимает полного единичного квадрата, мы можем аппроксимировать и найти ее значение. Если он занимает примерно 1/2 единицы площади, мы можем объединить две такие половины, чтобы образовать площадь в 1 квадратную единицу.
Обратите внимание на приведенный ниже рисунок.
Здесь площадь, занимаемая фигурой, равна 4 полным квадратам и 8 полуквадратам. Вместе это образует площадь 8 квадратных единиц. Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных фигур у нас есть определенные формулы для вычисления их площади. Обратите внимание, что это только приблизительное значение.
Площадь прямоугольника
Площадь прямоугольника — это площадь, занимаемая им. Рассмотрим желтый прямоугольник в сетке. Он занял 6 единиц.
В приведенном выше примере длина прямоугольника составляет 3 единицы, а ширина — 2 единицы. Площадь прямоугольника получается путем умножения его длины и ширины, что равносильно подсчету единиц квадратов. Таким образом, формула площади прямоугольника: : Площадь прямоугольника = длина × ширина. В данном случае это будет 2 × 3 = 6 квадратных единиц.
Площадь квадрата
Площадь квадрата – это занимаемая им площадь.
Посмотрите на цветной квадрат, показанный в сетке ниже. Он занимает 25 квадратов.
Из рисунка видно, что длина каждой стороны цветного квадрата равна 5 единицам. Следовательно, площадь квадрата – это произведение его сторон, которое можно представить по формуле: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.
Площадь круга
Круг представляет собой изогнутую форму. Площадь круга – это количество пространства, заключенного в границах круга. Узнайте больше о π и радиусе, прежде чем мы перейдем к формуле площади круга.
Площадь круга рассчитывается по формуле: π r 2 , где π – математическая константа, значение которой округляется до 3,14 или 22/7 и r — это радиус окружности.
Площадь геометрических фигур — Формула
Каждая форма имеет разные размеры и формулы. В следующей таблице показан список формул для площади различных фигур.
| Форма | Площадь фигур — Формула |
|---|---|
Квадрат | Площадь квадрата = x 2 квадратных единиц |
Прямоугольник | Площадь прямоугольника = длина × ширина = l × w квадратных единиц |
Круг | Площадь круга = π r 2 квадратных единиц |
Треугольник | Площадь треугольника = \(\dfrac{1}{2}\times b \times h\) квадратных единиц |
Параллелограмм | Площадь параллелограмма = основание × высота = b × h квадратных единиц |
Равнобедренная трапеция | Площадь равнобедренной трапеции = \(\dfrac{1}{2}(a+b) h\) квадратных единиц |
Ромб | Площадь ромба = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
Воздушный змей | Площадь воздушного змея = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
Ознакомьтесь со следующими темами, касающимися областей различной формы, и узнайте больше о формулах площади.
Советы и подсказки
Примеры на участке
Найдите его площадь. перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что».
Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по области
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Зоне
Что такое площадь?
Площадь фигуры представляет собой двумерную величину, которая измеряется в квадратных единицах, таких как квадратные дюймы или (в 2 ), квадратные футы или (футы 2 ), квадратные ярды или (ярды 2 ), и т.д.
Как найти площадь неправильной формы?
Площадь неправильной формы можно найти, разделив фигуру на единичные квадраты. Когда фигура не занимает весь единичный квадрат, мы можем аппроксимировать и найти ее значение.
Как доказать площадь круга?
Если окружность сложить в треугольник, радиус станет высотой треугольника, а периметр станет его основанием, равным 2 × π × r. Мы знаем, что площадь треугольника находится путем умножения его основания и высоты, а затем деления на 2, что составляет: ½ × 2 × π × r × r.
