Математическая палетка: Палетка для математики (3 класс): как сделать и как пользоваться?

Содержание

Как сделать палетку из бумаги — Строй Обзор

Содержание

  1. Методы изготовления
  2. Рекомендации по использованию
  3. Примеры вычислений
  4. Моря и земельные участки
  5. Палетка для математики
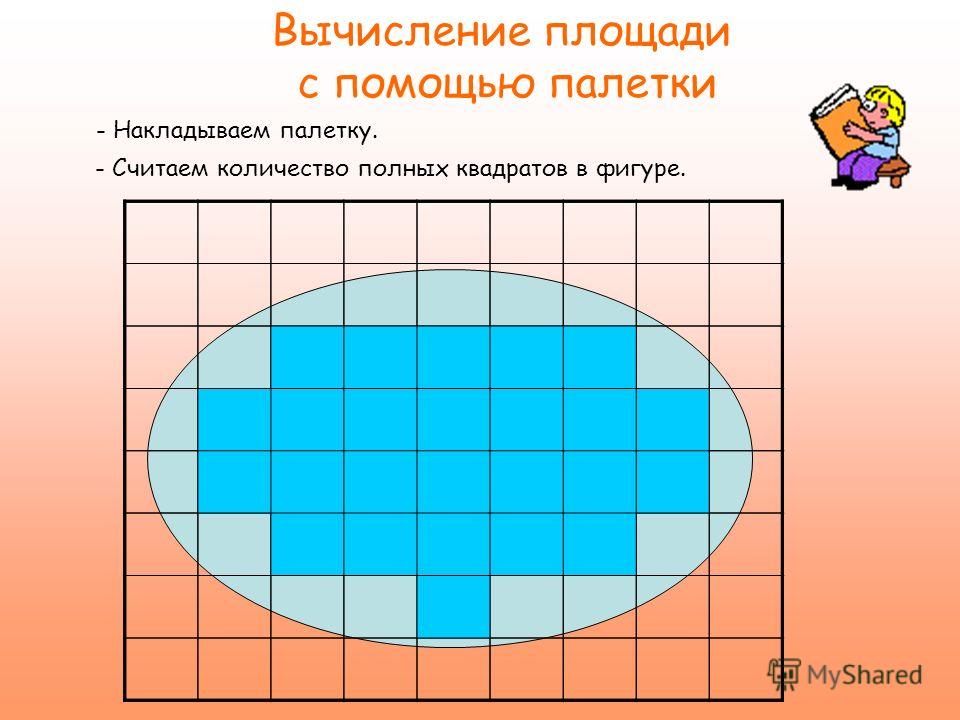
  6. Как пользоваться палеткой
  7. Формула площади фигуры с помощью палетки
  8. Видео как сделать палетку для математики
  9. Видео, как пользоваться палеткой, как посчитать площадь фигуры

Методы изготовления

Для математических вычислений площади сложных фигур правильно использовать заводской набор. В инструкции от производителя школьник может найти следующую информацию: для чего нужна палетка по математике, из каких материалов она изготовлена, как нужно её использовать. Внешне модель выглядит, как прозрачная пластина либо плёнка с разлиновкой в клетку.

С учётом параметров фигуры, площадь которой необходимо найти, образец разделяется на квадратные миллиметры, сантиметры, дециметры. Некоторые фирмы производят подобные инструменты с магнитной основой. Выбор зависит от предпочтений ребёнка и условий задачи.

Но можно сделать палетку по математике и своими руками.

Для этого потребуются следующие материалы:

Если предстоит работа с маленькими величинами, рекомендуется воспользоваться миллиметровой бумагой. Внешне самодельная палетка схожа на заводскую — расчерчена на клетки гибкого листа, предназначенного для нахождения площадей неправильных и правильных фигур, а также выполнения иных упражнений.

Самостоятельный шаблон будет стоить дешевле, чем заводской.

Кроме перечисленных материалов, потребуется прозрачная плотная полиэтиленовая обложка для дневника или тетради. Нужно измерить ее и расчертить ручкой на квадраты со сторонами 1 см. Данный шаблон будет иметь размеры 10х10 см. Если для изготовления применяется миллиметровка, рекомендуется обклеить её сверху скотчем, повторно расчертив клетки. Таким способом продлевается срок эксплуатации инструмента и дополнительно он защищается от влаги.

Чтобы сделать палетку площадью в 100 кв. см, потребуется придерживаться следующего алгоритма:

  • На листе в клетку отображается схема инструмента.
  • На палетку накладывается обложка.
  • Правильно обводятся клеточки. Чтобы инструмент выглядел аккуратно, используется линейка.
  • Вырезается готовый шаблон.

Рекомендации по использованию

Процесс измерения площади с помощью палетки простой, если она изготовлена правильно. Инструмент нужно приблизить к фигуре, наложив его сверху, и произвести расчет целых и неполных квадратов. Сложнее пользоваться палеткой, если все точки плоскости не поместились в неё.

В таком случае рекомендуется придерживаться следующего метода:

  • Разделить фигуру на части.
  • Произвести подсчёт каждой части отдельно.
  • Найти суммарный результат.

Рекомендуется подсчитывать отдельно, сколько целых квадратов вмещается в фигуру и сколько неполных. Площадь фигуры вычисляется по специальной формуле: S = количество целых квадратов (количество неполных/2). На уроках математики в начальной школе рекомендуется использовать палетку в виде прозрачного листка, на который нанесена сетка с квадратами (стороны по 1 см). Это объясняется тем, что в младших классах ученики работают с фигурами небольших размеров.

В современных учебниках по математике описаны подробные шаги по изготовлению и применению палетки. Рекомендуется использовать лист из тетради в клеточку. Из него вырезается самостоятельно школьником квадрат со сторонами 10х10 и ячейками в 1 см. Такой инструмент значительно упрощает работу, связанную с вычислением площадей фигур с неровными краями.

Очертания полученного шаблона обводятся чёрным маркером. Им же осуществляется дополнительная разметка составных квадратиков. Предполагается, что подобный метод значительно упростит и ускорит вычисления.

Школьнику будет легко и просто посчитать количество полных и неполных квадратов. Полученная палетка оборачивается с двух сторон скотчем либо самоклеющейся обложкой.

За счёт использования маркера отсутствует необходимость в повторной обводке прозрачного шаблона.

Чтобы школьнику было удобно понять, как получается математическое значение, палетку нужно наложить на неровно очерченную поверхность и подсчитать количества полных и неполных квадратов. В современных учебниках по математике первого понятие обозначается буквой P, а второе — N. Общий вид формулы: S=PxN/2.

Другой вариант записи: S=N+M/2, где

  • N — целые квадраты.
  • M — неполные квадраты.

Необходимо учесть, что полученный результат считается приблизительным, так как площадь и размер неполных квадратиков разная.

Примеры вычислений

В математике встречаются фигуры с неправильными границами, к примеру, овал. Для вычисления его площади понадобится палетка. Её нужно наложить сверху, подсчитав квадраты внутри границ овала. Предварительно подсчитывается количество целых клеток. Их вышло 34.

Кусочков насчитывается 8. Так как 8 — чётное число, поэтому два неполных квадрата можно засчитать за один целый. Если восемь разделить на два, получится четыре. Если к 34 добавить 4, получится 38. Площадь овала будет примерно равна 38 квадратиков или 38 квадратных сантиметров.

Задача: на тетрадь разлились чернила, появилось пятно. Чтобы выяснить, сколько клеток запачкалось, используется палетка. Так как пятно не имеет чёткой формы, поэтому накладывается сверху шаблон. При подсчёте выходит 17 целых клеток и 24 неполных.

Последнее число делится на два. К результату добавляется 17. Получается около 29 квадратных сантиметров. Другого алгоритма рекомендуется придерживаться, если количество клеток нечётное, к примеру, 30 либо 25. В таком случае на два нужно разделить ближайшую чётную цифру, но больше данного значения на единицу.

Моря и земельные участки

Палетка часто используется учениками на уроках географии. Чтобы найти площадь моря или озера, рекомендуется найти географический атлас либо карту с максимально возможным масштабом. Математический инструмент прикладывается к объекту.

Выполняются следующие шаги:

  • Считаются целые квадраты.
  • Затем — неполные.
  • Последний результат делится на два.
  • Полученное число суммируется с количеством целых квадратиков.
  • Записывается ответ.

Можно воспользоваться схемой и для расчёта площади страны, земельного участка, города. Чтобы выяснить примерную площадь местности, потребуется миллиметровая бумага. На ней с помощью карандаша приблизительно рисуется контур участка. Масштаб можно подобрать самостоятельно.

Современные педагоги и психологи считают, что с помощью палетки у детей формируется умение добывать информацию из текста. Дополнительно ученики начальной школы учатся формулировать и аргументировать свои мысли. За счёт шаблона развиваются вычислительные навыки при подсчёте площади разных геометрических фигур.

Плюсы развития операции логического мышления:

Используя палетку, ребёнок учится анализировать свою деятельность. Одновременно развиваются действия самоконтроля, взаимоконтроля, прививается аккуратность, точность при построении разных фигур. Палетка помогает ученикам научиться записывать правильно площадь, переводить одни единицы в другие, решать математические и географические задачи.

С её помощью дети учатся работать с геометрическими фигурами, соблюдая порядок выполняемых действий в числовых выражениях со скобками либо без них.

Палетка для математики

Палетка для математики — это прозрачный листок с нанесенной на нем ровной сеткой (квадратики одного размера, зачастую со стороной 1 см). Палетка предназначается для вычисления площади разных фигур (геометрических и других).

Прозрачная палетка

Также для вычисления площади можно пользоваться и не прозрачной палеткой, а просто расчертить схему сверху рисунка и таким образом получить необходимую информацию. Математическая палетка выглядит следующим образом:

Как пользоваться палеткой

Пользоваться палеткой для вычисления площади фигуры довольно просто. Нужно наложить сверху фигуры нашу палетку и начать считать сколько квадратиков поместилось в середине. Важно разделять сколько целых квадратиков поместилось и сколько частично попадают в фигуру.

Алгоритм расчета площади с помощью палетки:

  1. Накладываем палетку сверху фигуры, так чтоб вся фигура поместилась под расчерченной палеткой.
  2. Если фигура больше, тогда надо ее разделить на несколько частей и посчитать каждую отдельно, а потом посчитать суммарный результат.
  3. Считаем отдельно, сколько целых квадратиков вмещается в фигуру.
  4. Далее считаем количество неполных клеток
  5. Считаем площадь фигуры по следующей формуле:
    S= количество целых квадратиков + (количество неполных /2)

Формула площади фигуры с помощью палетки

Площадь фигуры по палетке

S= количество целых квадратиков + (количество неполных /2)

Пример на схеме, :

Видео как сделать палетку для математики

Видео, как пользоваться палеткой, как посчитать площадь фигуры

Распечатать палетку для измерения площади. Презентация по математике на тему «измерение площади фигуры с помощью палетки»

Сегодня ты узнаешь, как можно найти площадь новым способом.

Ответь на вопросы учителю (можно в видеокомнате).

  1. Вспомни, что такое площадь?
  2. В каких единицах она измеряется?
  3. Назови, какие геометрические фигуры ты знаешь?
  4. Площади, каких фигур ты умеете находить?
  5. Какие формулы ты можешь использовать для этого? Напиши их и покажи учителю. Можешь показать в видеокомнате или написать на .

А можешь ли ты найти площадь треугольника?

Знаешь ли ты формулу, которая может тебе помочь решить эту задачу?

Сейчас ты не знаешь эту формулу. Тебе расскажут о ней в старших классах.

И все же попробуем решить эту задачу.

На рисунке 1 дан прямоугольник. Указаны его размеры и площадь S = 200 кв. ед .

Предложи варианты нахождения площадей треугольников, указанных на рисунке 2.


Запиши свои решения в тетради и объясни их учителю (можно в видеокомнате).

Итак, ты смог найти площадь прямоугольного треугольника. Предложенный тобой способ справедлив только для этого вида треугольников.

Но они бывают разные. Поэтому нам нужно познакомиться с новым способом нахождения площадей.

Сегодня на уроке ты будешь учиться находить площадь фигур с помощью .

Давай научимся определять площадь с помощью палетки.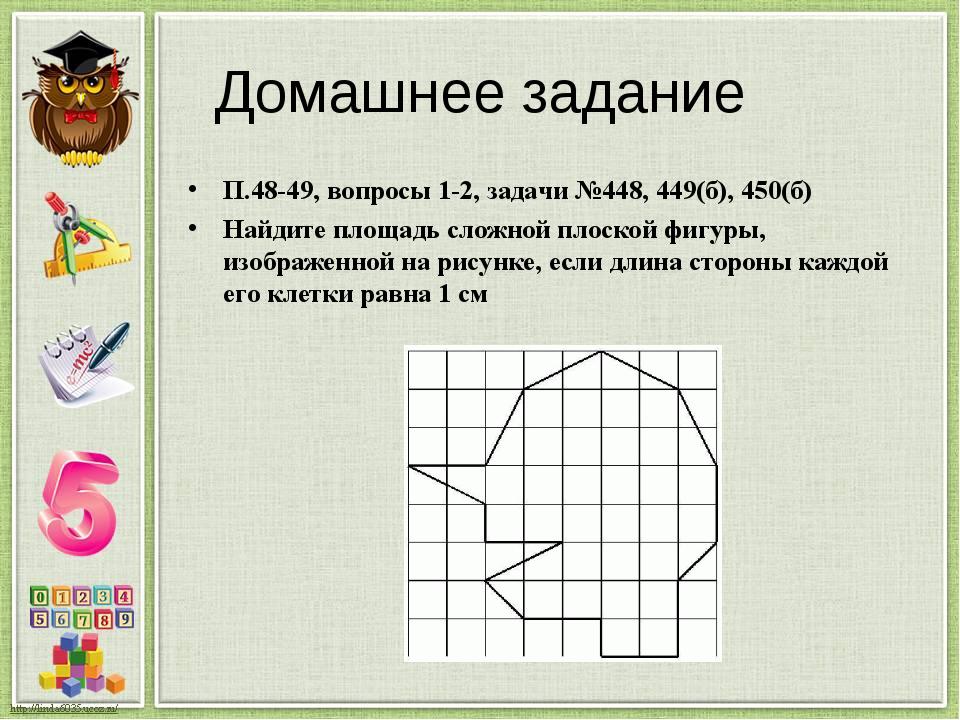

Рассуждения:

  1. Одна длина стороны прямоугольника равна 3 см.
  2. В три сантиметра укладываются 3 стороны маленького квадратика.
  3. Следовательно длина стороны квадратика равна 1 см (3 см: 3 = 1 см).
  4. Другая длина стороны прямоугольника равна 5 см.
  5. В пять сантиметров укладываются 5 сторон маленького квадратика.
  6. Следовательно длина стороны квадратика равна 1 см (5 см: 5 = 1 см).
  7. Делаем вывод, что действительно у нас квадратики со стороной 1 см.
  8. Площадь этого маленького квадратика равна 1 см 2 .
  9. Считаем, сколько квадратиков внутри прямоугольника. Их 15.
  10. Поэтому площадь прямоугольника будет равна: 1 см 2 · 15 = 15 см 2 .
  11. Значит правильный ответ у Коли.

Познакомься с алгоритмом нахождения площади фигуры с помощью палетки.

Посмотри и повтори , как можно использовать палетку для нахождения площади фигуры произвольной формы.

Рассмотрим пример нахождения площади геометрической фигуры с помощью палетки.

Поурочный план открытого урока

Предмет: математика.

Тема:»Измерение площади фигуры. Палетка».

Цели:

· Познакомить детей со способом нахождения площади фигур различной формы с помощью палетки.

· Учить анализировать геометрические фигуры.

· Развивать логическое мышление учащихся, умение точно и обоснованно аргументировать, выделять те стороны наблюдаемых явлений, которые необходимы для с исследования и осмысления задачи.

· Совершенствовать умение решать задачи.

· Воспитать интерес к предмету, любознательность, дружеское отношение к одноклассникам в совместной работе.

Задачи урока: Создать условия для самостоятельного поиска знаний.

Оборудование: «Измерение площади фигуры с помощью палетки»,презентация

Дидактические материалы к учебному занятию:

Ход учебного занятия

1.Организационный момент :

Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте,
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?

Каждый хочет получать
Лишь оценку «5»?

2. Сообщение темы урока

Учитель: Ребята, мы вновь погружаемся в мир нескучной математики. Сегодня познакомимся с геометрическими фигурами, площадь которых находим новым способом. А каким, узнаем на уроке. У нас всё получится.

3. Оформление работ в тетрадях.

Математика — царица всех наук. Она нужна в любой науке, в любой профессии, например, археологам. Вы знаете, кто такие археологи? Посмотрим презентациию «Кто такие археологи».

7. Работа по индивидуальным карточкам.

Нахождение площади фигур прямоугольной и квадратной формы.

Поиграем в эту профессию. Вы приехали на раскопки. Вам необходимо определить, какова площадь участка земли прямоугольной или квадратной формы, на которой вы будете что-то искать. (У каждого карточка с чертежом, данными. Дети по формуле находят площадь, делают чертёж и запись в тетрадь.)Один ученик у доски.

S = 5* 9= 45 м2

ПРОВЕРКА. Учитель раздаёт карточки, на которых указан верный ответ, дети зачитывают свои ответы — Отогните ответы и вы увидите, археологи, кого вы откопали. Динозавров..jpg»>.jpg»>

8 . Физминутка

Вы наверное устали?
-Да!
— И поэтому все встали.
Дружно вытянули шеи
как динозавры зашипели:, зарычали.
Пошипели, помолчали
как динозавры, поскакали.
Поскакали, поскакали
И за кустиком пропали.

9. Знакомство с новой темой.

Я вот такого динозавра нашла.(На доску вывешен плакат.)

— Можем мы найти его площадь по формуле? Почему?

Существует способ нахождения площади фигур неправильной формы с помощью палетки – плёнки прозрачной с нанесенными на ней квадратными сантиметрами.

10. Знакомство с презентацией «Палетка»

11. Работа по теме урока

Нахождение площади динозавра по алгоритму . используя большую палетку. Учитель комментирует.

Алгоритм вычисления площади с помощью палетки

1. Наложи палетку.

2. Посчитай количество

полных квадратов в фигуре.

3. Посчитай количество неполных квадратов и раздели это число на 2:

4. Сложи количество полных квадратов и число неполных квадратов, делённое на 2.

Дети делают запись в тетрадь.

12. Физминутка. (Парный танец)

Давай, Дино, попрыгаем, попрыгаем. попрыгаем.

И ножками подрыгаем, подрыгаем, подрыгаем.

13. Самостоятельная работа. Найди площадь яйца с помощью палетки.

А вы знаете, как появляются на свет маленькие динозаврики? Из яиц. Продолжим наши археологические раскопки. Кто найдёт в пределах расчерченных на полу квадратных метрах яйцо динозавра, имеет право в него посмотреть.

(Дети находят по «яйцу» от киндера, внутри каждого – палетка и надпись «палетка»)

Учитель раздаёт рисунки яйца, просит найти его площадь. Дети самостоятельно находят площадь яйца с помощью палетки.

14. Тестирование.

Проверим наши знания. В тесте обведите в кружок правильный ответ.

ТЕСТ по теме «Палетка»

1. Прямоугольник, у которого все стороны равны, называется

Треугольник

2. Чтобы найти площадь квадрата или прямоугольника, нужно

Длину умножить на ширину

Найти сумму всех сторон.

3. С помощью палетки площадь находят так:

Сложи количество полных квадратов и число неполных квадратов, делённое на 2.

Длину умножить на ширину

4. Единицы измерения площади:

Мм см м к м

Мм2 см2 м2 к м2

5. Формула площади квадрата или прямоугольника

15 . РЕЗЕРВ .

Работа в группах.

1 группа пишет названия предметов, площадь которых удобно находить по формуле

2. группа пишет названия предметов, площадь которых удобно находить палеткой.

16. Итог урока. Комментирование оценок.

Ч то нового узнали на уроке?

Что понравилось?

17. Домашнее задание.

С помощью палетки находи площади мелких предметов, рисунков.

Для определения на плане площадей небольших участков с криволинейными контурами применяют прямолинейные и кри­волинейные палетки.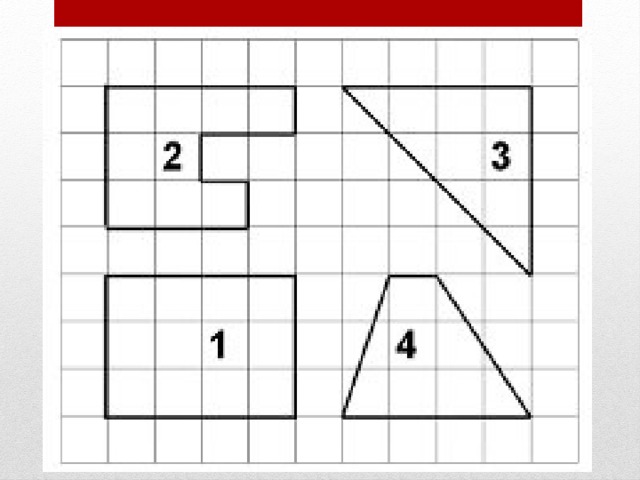 К прямолинейным относят известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет сеть взаимно перпендику­лярных линий, проведенных через 1 мм на прозрачном целлулои­де, плексигласе, фотопленке, стекле или восковке (рис.1.1, а). Площадь фигуры вычисляют простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитывают на глаз. Как видно на рисунке 5.2, а, площадь контура занимает 58 клеток 1 . Для плана масштаба 1:10 000 пло­щадь клетки со стороной 1 мм равна 10×10= 100 м 2 = 0,01 га. Сле­довательно, площадь контура равна 0,58 га.

Для упрощения подсчетов проводят утолщенные линии через 0,5 и 1 см, чтобы число клеток можно подсчитать сразу группами (25 и 100 мм 2).

Недостаток ее применения помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз, со­стоит еще в том, что подсчет числа целых клеток нередко сопро­вождается грубыми ошибками.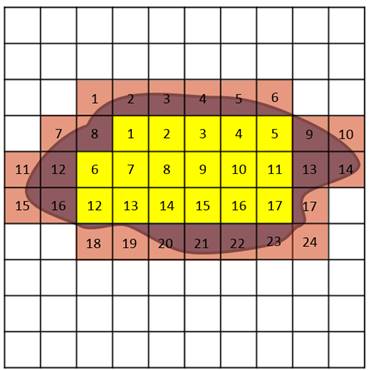

Таких недостатков не наблюдается при определении площадей параллельной палеткой, представляющей собой листок прозрачно­го целлулоида, плексигласа или восковки, на котором нанесены параллельные линии, проведенные преимущественно через 2 мм одна от другой (рис.1.1, б).

Площадь контура этой палеткой вычисляют следующим обра­зом. Накладывают ее на контур так, чтобы крайние точки а и b разместились посередине между параллельными линиями палет­ки. Таким образом, весь контур оказывается расчлененным парал­лельными линиями на фигуры, близкие к трапециям с одинако­выми высотами, причем отрезки параллельных линий внутри кон­тура являются средними линиями трапеций. Прерывистыми ли­ниями на рисунке 1.1 , б показаны основания этих трапеций. Сумма площадей трапеций, т. е. площадь контура,

P=cdh + efh + mnh + … + klh.

Так как все высоты трапеций равны,

P=h(cd+ef+mn + … + kl)

Рис. 1.1 – Определение площади контура квадратной (а) и параллельной (б) палетками

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т. е. сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля: сначала берут отрезок cd, затем, не сжимая циркуля, совмещают левую его ножку с точкой /(см. рис. 5.2, б). После этого, не сдвигая правую ножку циркуля с места, увеличивают раствор циркуля, установив левую ножку в точку е. Таким образом, в растворе циркуля получают отрезок, равный cd + ef. Далее левую ножку циркуля устанавливают в точку л, вследствие чего пра­вая ножка встанет от точки п на расстоянии cd + ef После этого, не сдвигая пра­вую ножку с места, раствор циркуля увеличивают, установив левую ножку в точку т, и т.д. Последним отрезом, набираемым в раствор циркуля, будет отрезок к). Набранную в раствор циркуля сумму средних линий определяют по масштабной линейке, и полученную длину умножают на расстояние Л, соответствующее числу метров на местности.

Например, если масштаб плана 1:10 000, h – 20 м и сумма сред­них линий равна 682 м, то площадь контура будет равна 13 640 м 2 , или 1,36 га. Чтобы не выполнять подобных вычислений, для нуж­ного масштаба плана строят специальную шкалу, по которой от­считывают площадь контура, зная сумму средних линий. Рассчи­таем основание шкалы для масштаба 1:10 000. При расстоянии между параллельными линиями 2 мм и при основании шкалы 1 см площадь будет равна 20 100 = 2000 м 2 = 0,20 га. Следовательно, каждому сантиметру шкалы будет соответствовать 0,20 га на мест­ности. Левое основание шкалы делят на 10 частей, как это делают при построении линейного масштаба (см. рис. 1.1 , б).

Основанию масштаба 1:25 000, равному 1 см, будет соответство­вать площадь 1,25 га. Такое основание неудобно для определения площадей, поэтому следует рассчитать основание, которому соот­ветствует площадь 1 га. В этом случае длина основания, очевидно, будет равна 0,8 см. Левое основание шкалы также делят на 10 час­тей.

Для масштаба 1:5000 основание принимают 2 см, которое будет соответствовать площади 0,1 га.

После того как сумма средних линий в раствор циркуля набра­на, определяют площадь по шкале так же, как расстояния по ли­нейному масштабу. Палетку и шкалу обычно строит сам исполни­тель. Параллельной палеткой не следует определять площади больше 10 см 2 на плане.

К криволинейным относят гиперболические палетки, представляющие систе­му гиперболических кривых и применяющиеся для определения площадей про­стейших геометрических фигур. Эти палетки не находят заметного распростране­ния, так как при помощи их нельзя быстро определить площадь участка с криво­линейным контуром.

Для определения площадей небольших участков с криволинейными контурами на плане применяют палетки, в основном прямолинейные. К прямолинейным палеткам относятся известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет собой сеть взаимно перпендикулярных линий, проведенных через 1–2 мм на прозрачном целлулоиде, плексигласе, фотопленке, стекле или кальке.

Площадь фигуры определяется простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитываются на глаз (рис. 13). Квадратной палеткой не рекомендуется определять площади больше 2 см 2 на плане. Недостаток ее применения (помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз) в том, что подсчет количества целых клеток нередко сопровождается грубыми погрешностями.

Такие недостатки не наблюдаются при определении площадей параллельной палеткой, представляющей собой листок прозрачного целлулоида, плексигласа или кальки, на котором нанесены параллельные линии преимущественно через 2 мм одна от другой. Площадь контура определяют этой палеткой следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посредине между параллельными линиями палетки. Тогда, весь контур оказывается разделенным параллельными линиями на фигуры, близкие к трапециям, с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций (рис.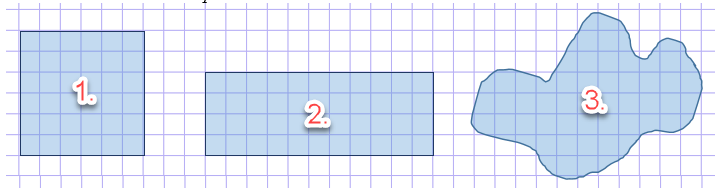 14). Пунктиром показаны основания этих трапеций.

Сумма площадей трапеций, т.е. площадь контура, равна

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т.е. сумму отрезков параллельных прямых внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля, которую определяют по масштабной линейке и полученную длину умножают на h , м (рис.15). Чтобы не выполнять подобных вычислений, для каждого масштаба строят специальную шкалу, по которой отсчитывают площадь контура, зная сумму средних линий.

Расчет шкалы: М 1:10000, h = 2 мм, при длине шкалы 1 см площадь равна (0.2 см  100 м)  (1 см  100 м) = 2000 м 2 = 0.2 га. Параллельной палеткой не следует определять площади больше 10 см 2 на плане.

При разбивке участка на простейшие фигуры точность вычисления для различных вариантов не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее, чем площади других фигур. Следовательно, площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на другие фигуры (трапеции, прямоугольники). При разбивке участка на треугольники из всех вариантов будет лучшим тот, в котором треугольники будут равносторонними или высота h примерно равна основанию a .

Погрешность уменьшается, если вычислять площадь треугольника не как
, а по формуле Герона

где
. Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане.

Урок-путешествие по станциям в рамках Недели математики. 3–4-й классы

Урок-путешествие ставит перед собой цель:

  • обобщить и закрепить знания и умения учащихся математического и геометрического характера;
  • способствовать овладению математическими понятиями и терминами;
  • развивать познавательного интереса к предмету «математика»,
  • формировать умения работать в бригадах;
  • развивать организационные общеучебные умения, в том числе, умение оценивать результат своей работы, умение концентрировать внимание, формировать и обосновывать свои высказывания, слушать и понимать высказывания товарищей.

Для проведения мероприятия понадобится оборудование: «Математическая палитра», 4 карточек с упражнениями на внимание, (из пособия «Спектр математика») пирамида на умножение и деление, конверты с заданиями для команд, маршрутный лист для каждой команды, название станций, палетка, кроссворды математический, ноутбук для детей, компьютер и проектор для учителей.

После проведения такого урока больше детей изъявили желание участвовать в математических викторинах и конкурсах.

Оборудование: «Математическая палитра» , 4 карточки с упражнениями на внимание, из пособия «Спектр математика» пирамида на умножение и деление, конверты с заданиями для команд, маршрутный лист для каждой команды, название станций, палетка, математический кроссворд, ноутбук для детей, компьютер и проектор для учителей.

План урока:

  1. Вступительное слово.
  2. Путешествие по станциям.
  3. Подведение итогов. Награждение экипажей победителей.

I. Вступительное слово учителя.

Учитель 1: Предмет математики настолько серьёзен, что необходимо не упускать возможности делать его немного занимательнее» говорил Блез Паскаль. Сегодня мы с вами сделаем урок математики немного занимательнее.

Учитель 2: Мы предлагаем вам, принять участие в «Путешествие за числом и точкой».

Учитель включает презентацию (Приложение 9).

Учитель 1: Путешествие пройдёт по восьми станциям для каждого экипажа. На каждой станции вы останавливаетесь только на 5 минут. По сигналу учителя вы должны прекратить работу и перейти на другую станцию, которая записана у вас следующим номером.

Учитель 2: Во время работы на второй станции учитель проверит вашу работу на предыдущей станции и впишет количество заработанных баллов.

Учитель 1: На ваших маршрутных листах указано, сколько баллов вы можете заработать на каждой станции.

Учитель 2: Экипажи, набравшие наибольшее количество баллов получают грамоты и призы.

(Определяют победивший экипаж в каждом классе отдельно)

Учитель 1: Для того чтобы начать, необходимо поделиться на экипажи. Проведем жеребьёвку.

(Из мешочка дети берут геометрические фигуры и по цвету объединяются в экипажи)

Учитель 2: Капитаны экипажей подойдите и возьмите конверты с маршрутом путешествия своей команды.

Маршрутный лист первого экипажа 3 «Г» класса.

Станция Задание Успешность

1. «Измерялкино»

 Кот
котёнок		  

2. «Соединялкино»

 Кроссворд
Узнай фигуру		  
3. «Рисункино» Палитра
Избушка		  
4. «Оригамкино» Волк  
5.»Задачкино» Огород  
6.«Отгадайкино» Кроссворд математических терминов  
7.»Собиралкино» Пирамида   
8.«Считалкино» Числовой сканворд  
Всего    

(Аналогичные маршрутные листы для других экипажей только станции в другой последовательности)

Учитель 1: Вас ждут задания геометрической направленности и математической. Станции «Измерялкино», «Соединялкино», «Рисункино», «Оригамкино» находятся в 23 кабинете.

Учитель 2: Станции «Задачкино», «Отгадайкино», «Собиралкино», «Считалкино» в кабинете №25.

Учитель 1: Желаем удачи!

(Задания геометрической направленности одинаковые для двух классов, а математической — разные, с учетом прохождения программы, для 3 и 4 классов)

Первый этап путешествия в 23 кабинете.

Учитель 1: Юные математики, прежде, чем мы начнем наше путешествие, мы проведем блицтурнир личного первенства. Внимание на экран.

Учитель проводит блиц-турнир презентация (Приложение 10)

После блицтурнира детям, набравшим больше баллов, дарят призы.

1. «Измерялкино»

Задание. Вычислите площадь рисунка кошки.

(Можно воспользоваться палеткой или найти через площади геометрических фигур.)

(Приложение 1)

Оценивание.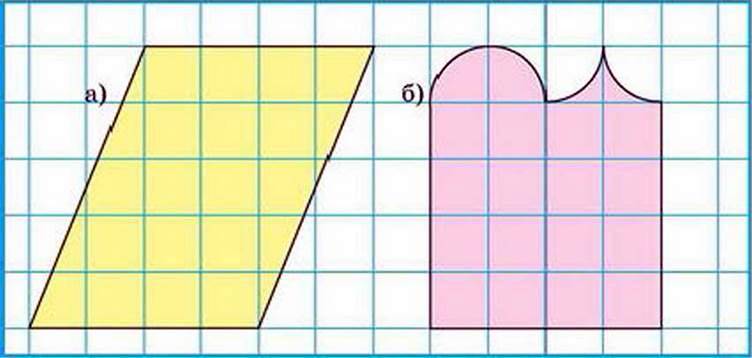 5 баллов – если найдены величины площади на двух рисунках, 3 балла – если определена площадь одного рисунка.

2. «Соединялкино»

Задание. Соедините название геометрических фигур с их определением

(Задание на ноутбуке в программе HotPotatoes – Приложение 8)

Оценивание. 5 баллов — за правильное соединение название геометрических фигур с определением, если допущена одна ошибка – вычитаем 1 балл).

3. «Рисункино» (Приложение 2, 3)

Задание. 1. Работа с математическими палитрами. Найди такой же рисунок. Игра на внимание. 2. Выберите три изображения избушки, когда она начнёт поворачиваться.

Оценивание. 5 баллов – все кружки совпали, одинаковые изображения найдены верно. 5 баллов за правильно найденные изображения избушки.

4. «Оригамкино» (Приложение 4)

Задание. Из двух квадратов 15 х 15 см и 10 х 10 см по заданному алгоритму сделать «Волка».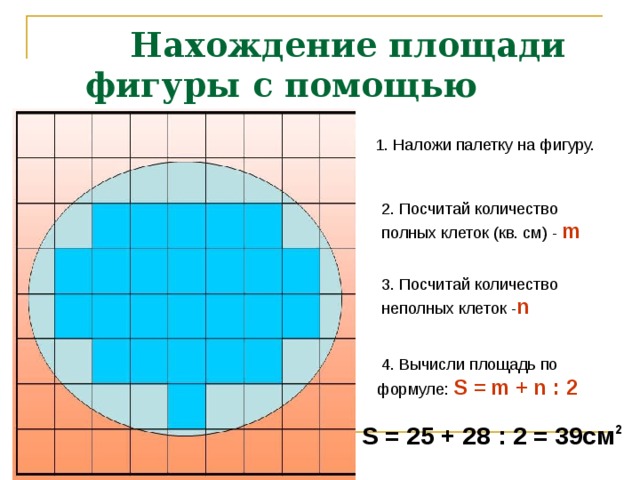

Оценивание. За каждого волка получаем 2 балла.

Второй этап путешествия – 25 кабинет

Задания математической направленности для 4 «Г»

5. «Собиралкино»

Задание. Собираем пирамиду на «Внетабличное умножение и деление»

Оценивание. За 5 минут нужно как можно больше решить выражений на умножение и деление. Соединить выражение с ответом. Количество баллов соответствует количеству решенных выражений.

6. «Считалкино» (Приложение 5)

Задание. Решить числовой сканворд.

Оценивание. 1 балл за каждое выражение, выполненное верно.

7. «Отгадайкино» (Приложение 6)

Задание. Решение понятийного кроссворда.

Оценивание. 1 балл за каждое определение (понятие), выполненное верно.

8. «Задачкино» (Приложение 7)

Задание.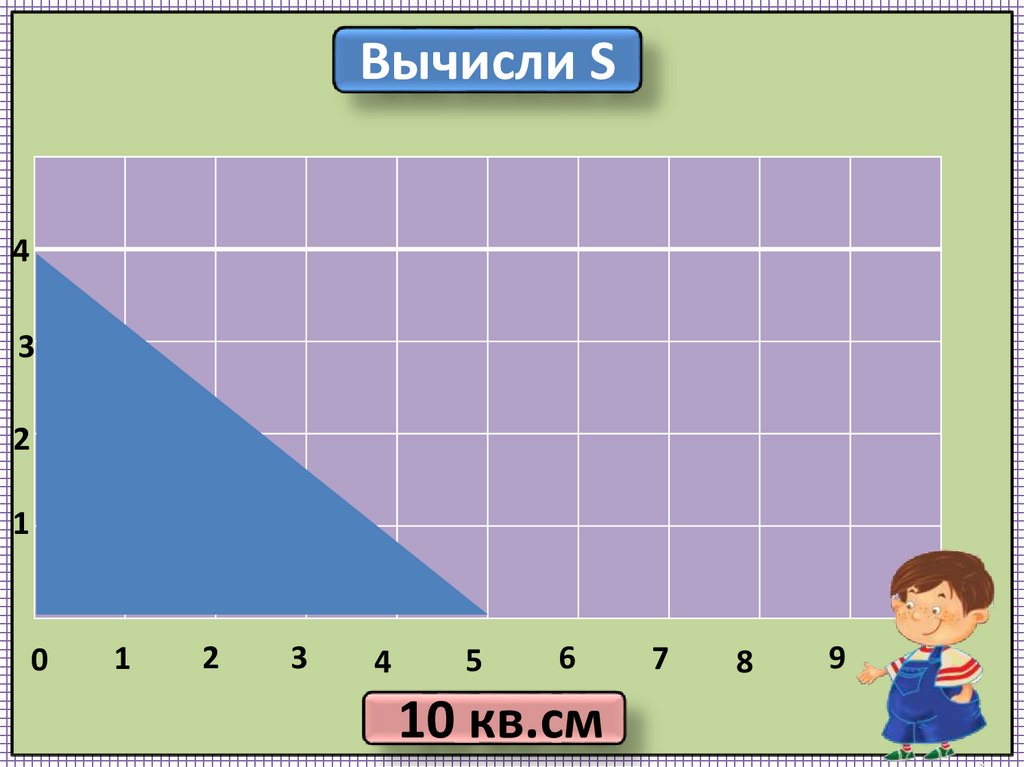 Решить задачи любым способом: по действиям, выражением, уравнением, путём рассуждений.

Оценивание. 5 баллов за правильное решение.

Задания математической направленности для 4 «Б»

1. «Собиралкино»

Задание. Собрать пирамиду на внетабличное умножение и деление. За 5 минут нужно как можно больше решить выражений на умножение и деление. Соединить выражение с ответом.

Оценивание. Количество баллов соответствует количеству решенных выражений.

2. «Считалкино»

Задание. Найти нужные числа.

  • Сумма двух чисел равна 385. Одно из них оканчивается нулём. Если зачеркнуть 0 в трёхзначном числе, то получится другое число. Какие это числа?
  • В каждой цепочке чисел найди закономерность и вставь пропущенные числа.
    3, 6, …, 12, 15, … , …, 24;
    1, 8, 11, 18, …, 28, 31, …,…, 51;
    45, 36, 28, 21, …, 10, 6.

Оценивание. По 5 баллов за каждое задание.

3. «Отгадайкино»

Задание. Каждая буква в алфавите представлена каким- то числом. А… Б… В… Г… Д… Е… Ё… Ж… З… И… Й… К… Л… М… Н… О… П… Р… С… Т… У… Ф… Х.. Ц…Ч.. Ш… Щ … Ъ… Ы… Ь… Э… Я…

Попробуй определить эти числа (найти код), если слово ГИД записывается, как 6, 12, 7, а слово СОН, как 21, 18,17;

Попытайся при помощи этого кода прочитать фразу 16 18 15 18 7 8 26 17 3 227 12 3 13 7 20 23 6 23 24 21 22 20 3 17 12 26 23;

Оценивание. 5 баллов.

4. «Задачкино»

Задание. Решить задачи.

  • Гном разложил свои сокровища в 3 сундука разного цвета, стоящие у стены: в один – драгоценные камни, в другой – золотые монеты, в третий – магические книги. Он помнит, что красный сундук находится правее синего сундука. В каком сундуке лежат книги, если зелёный сундук с драгоценными камнями стоит левее синего.
  • Родительский комитет купил на покраску пола в классе 4 банки краски, по 3 кг в каждой. Длина класса – 8 м, ширина – 6 м. Хватит ли этой краски на покраску пола в классе если на каждый 1 кв. м расходуется по 250 г краски?
  • Какой толщины будет альбом в 80 страниц, если каждые 5 листов имеют толщину 2 см?

Оценивание. За верное решение каждой задачи по 5 баллов.

III. Подведение итого. Награждение экипажей победителей.

После прохождения всех станций экипажи строятся на линейку. Учителя объявляют количество баллов, которое набрал каждый экипаж. Победителям вручают грамоты и призы.

Литература:

  1. А. В. Кочергина, Л.И. Гайдина Учим математику с увлечением , 1 – 4 класс, 2-е изд. – М.: 5 за знания, 2008.
  2. «Я иду на урок в начальную школу» Внеклассная работа. Олимпиады и интеллектуальные игры. Книга для учителя. Москва «Первого сентября», 2000.
  3. Марченко И. С. Математика: 4 класс. Реши задачу: для любознательных. – М.: Эксмо, 2009.
  4. Жильцова Т. В., Обухова Л. А. Поурочные разработки по наглядной геометрии: 1-4 класс. – М.: Вако, 2004.

Приложения 1–7.

Редактирование математики в Amaya

Amaya предлагает интерфейс Wysiwyg, в котором математические выражения MathML обрабатываются как структурированные компоненты так же, как элементы (X)HTML. Таким образом, вы можете манипулировать математическими выражениями так же, как вы манипулируете другие части (X)HTML-документов. Все команды редактирования, предоставляемые Amaya для обработка текста также доступна для математики, но есть некоторые дополнительные элементы управления для ввода математических конструкций. Обратите внимание, что разные браузеры не ведите себя так же с MathML: см. браузеры раздел совместимости для получения дополнительной информации.

Создание математических формул

Новая формула

Как правило, математические формулы не сами по себе, а включаются в документ с текстом, таблицей, изображениями. .. для этого вам нужно создать документ XHTML. В противном случае вы можете создать документ MathML (mml), например, для использования формулы в других программных средствах. Для этого используйте команду File/New/ Новая формула или введите Ctrl-n Ctrl-m .

Чтобы создать новое математическое выражение в документе, переместите точку вставки в то место, где вы хотите вставить выражение, а затем щелкните значок Математика кнопка (первая) в палитре Math или выберите Вставить формулу из подменю Insert/Math . Вот примеры с формулой вставляется непосредственно в документ XHTML или внутри изображения SVG:

Γ⁡(x)=∫0+∞tx−1ⅇ−tⅆt

Γ⁡(x)=∫0+∞tx−1ⅇ−tⅆt

Подменю Insert/Math включает презентацию MathML элементы.

  • Первые элементы создают новые элементы заданного типа в математическом выражение : Обычный текст (mtext) , Идентификатор (мили) , Номер (мн) , Оператор (мес) . Эти команды также могут изменить тип отдельного элемента. или последовательность элементов.
  • Следующая команда, Space (mspace) , позволяет добавить пробел в формуле. Чтобы изменить его размер, вы должны изменить его ширина атрибут. См. интервал.
  • Следующий элемент, Символ (&xxx;) , позволяет вам введите символ, которого нет на клавиатуре. Он отображает диалоговое окно, в котором вы должны ввести имя персонажа (например, альфа для греческого символа α).
    Обратите внимание, что вы также можете использовать инструмент Специальные символы (команда Виды / Показать/скрыть панели инструментов / Специальные символы ).
  • Две следующие команды InvisibleTimes и ApplyFunction используются для ввода соответствующих невидимые персонажи. Смотрите специальные символы раздел.

Следующие пункты подменю Insert/Math позволяют вам создавать новые конструкции в формуле.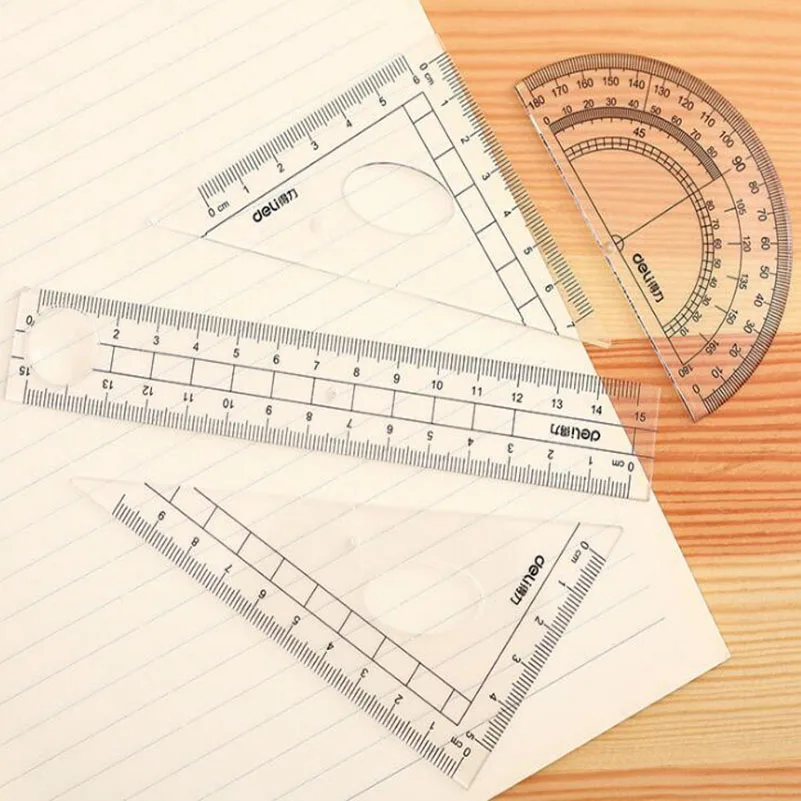 Если точка вставки находится не в Формула Amaya сначала создает математический элемент для принятия нового построить. Доступны следующие конструкции:

Математическая палитра

При нажатии кнопки на математической палитре вставляется математическая конструкция представлен на его значке. Детали черного цвета действительно вставлены, детали красного цвета представляют собой заполнитель, части, выделенные синим цветом, запрашиваются в определенном диалоговом окне. Зеленые части — это просто дополнительная информация, которая не вставляется.

Палитра содержит все конструкции, описанные в Content MathML (но полученный код является эквивалентом в Presentation MathML, см. раздел известных проблем) и даже больше. Вы также можете сохранить свой собственные конструкции в файле mml, чтобы использовать их последними. 6 вкладок:

    • отношения эквивалентности и порядки
      • равенства, приближенные, конгрю, изоморфные
      • неравенства
      • инф, доп, макс и мин
    • логика
      • Правда и Ложь
      • эквивалент
      • универсальные и экзистенциальные кванторы
      • not, and, or, xor, подразумевает эквивалент
    • теория множеств
      • набор/список, созданный расширением/разделением, nuple
        • элемент
      • , подмножество
      • пустой комплект, powerset
      • дополнение, разность, симметричная разность
      • пересечение, объединение, декартово произведение
      • кардинал, омега, алеф, диагональное пересечение
    • функции и карты
      • лямбда-конструкция
      • определение карты, стрелки
      • домен, изображение (диапазон), кодовый домен
      • тождество, составление, инверсия
    • арифметика
      • сумма, товар
      • факториал, комбинация, кардинальное число
      • коэффициент
      • лкм, НОД
      • напоминание, частное
    • операций
      • элементарные операции: плюс, минус, умножение, деление, дробь
        • мощность
      • , корень
      • пол, потолок
    • комплексы
      • абс, арг, конъюгат
      • декартово, полярно
      • действительная и мнимая часть
    • константы: ⅇ, ⅈ, π, γ, NaN (не число)
    • анализ
      • дифференциал, частичный дифференциал
      • интегралы: простой/двойной/тройной, нормальный/контурный, msub/msupsub
      • эквивалент
        • предел
      • , стремится к
      • супминус (1-) или супплюс (0+)
      • бесконечность
      • О и О
    • линейная алгебра
      • прямая сумма
      • векторная строка, векторный столбец, матрица
      • транспонирование, определитель
      • завиток, деление, град, лапласиан
      • векторное произведение, скалярное произведение, внешнее произведение
      • ортогональное, параллельное, ортогональное дополнение, норма
    • статистика: среднее, sdev, дисперсия, медиана, мода, момент
  6. классические элементарные функции (тригонометрические, обратные. ..)
Ввод математических конструкций с помощью клавиатуры

Вы не обязаны использовать подменю Math или Математическая палитра для создания и редактирования математических выражений. Ты можно вводить математические конструкции прямо с клавиатуры, потому что каждый ввод подменю Math имеет клавиатурный эквивалент. Эти ярлыки перечислены в меню. См. список текущих ярлыков для Linux, Mac OS X и Windows.

Вы также можете использовать клавиши со стрелками на клавиатуре для перемещения точки вставки из одну математическую конструкцию к другой. Стрелки вправо и влево перемещают вставку точку в соответствии со структурой математического выражения. Например, в дроби, когда точка вставки стоит в конце числителя, справа Клавиша со стрелкой перемещает точку вставки в начало знаменателя. Кроме того, если вы используете правую стрелку для конструкции, которая еще не завершена, точка вставки перемещается непосредственно к ближайшему местозаполнителю.

Дополнительные функции редактирования

Ввод математических символов

Когда вы вводите строку символов в элементе MathML, Amaya анализирует строка и автоматически генерирует элементы mo (оператор), мн (номер), ми (идентификатор) и мтекст .

Например, чтобы ввести формулу x=2a+b

  1. Если вы не находитесь в математическом выражении, выберите Вставить формулу из Вставка/Математика подменю.
  2. Введите последовательность из 6 символов: x=2a+b

Используйте представление структуры или исходного кода для отображения следующей структуры сгенерировано Amaya:

x=2a+ b

Если результат не совсем то, что вы хотите, выберите символы, которые были неправильно истолкованы и изменить их тип с помощью одной из команд, таких как Простой текст (mtext) , Идентификатор (mi) , Номер (мн) , Оператор (мн) или Пробел (м пробел) .

Конструкция строки

Конструкция строки из палитры эквивалентна фигурные скобки в LaTeX: это позволяет вам давать информацию о том, как различные части формулы группируются вместе. Он не появляется на экране, но косвенно влияет на визуализацию.

Например, при вводе квадратных скобок в следующем выражении:

f⁡(x)=1x

ввод последовательности f(x)= ... приведет к:

f⁡(x)=1x

Здесь (x) должно содержаться в элементе mrow . Вы можете исправить проблему, выбрав эту часть формулы, а затем нажав на конструкцию строки. Вы также можете напрямую получить ожидаемый mrow если выбрать Скобки из Insert/Math подменю или выберите кнопку в Math палитра .

Интервал

Amaya заботится о интервалах в математических выражениях, но в некоторых случаях вы возможно, потребуется добавить дополнительное пространство. Переместите курсор в положение, где вы хотите вставить пробел и выберите Space (mspace) из Подменю Вставка/Математика . Это создает горизонтальное пространство по умолчанию. Затем вы можете изменить его атрибут width , чтобы настроить его размер, или вы можно добавить другие атрибуты ( высота , глубина , разрыв строки ), чтобы изменить интервал по вертикали. Обратитесь к MathML Спецификация для более подробной информации.

Специальные символы

Вы можете использовать команду Символ из подменю Insert/Math для ввода математических символов и символы, которых нет на клавиатуре. Введите название символ, как определено в MathML Технические характеристики. Вы можете ввести значение Unicode символа вместо. Для ввода этого значения в десятичном виде начните с «#». Для входа в значение в шестнадцатеричном формате, начинающееся с ‘#x’. Чтобы печатать быстрее, вы также можете ввести шестнадцатеричное значение без ведущего ‘#x’, но обратите внимание, что это может быть двусмысленным (например, «аф»). В случае неоднозначности строка интерпретируется как название характера.

Вы также можете использовать инструмент Специальные символы . В этом инструменте раскрывающееся меню позволяет выбрать группу символов, которые затем доступны в таблице ниже. Щелкните символ в этой таблице, чтобы вставить его в формуле или где-либо еще в документе.

Также спецификация MathML рекомендует добавлять невидимые символы в чтобы облегчить синтезатору речи чтение формулы. Эти символы автоматически вставляются из палитры, но иногда у вас сделать это самостоятельно. Затем вы можете использовать Вставка/Математика подменю или ярлыки. Три невидимых персонажа являются:

  1. невидимые времена: a⁢b
  2. применить функцию: f⁡(x)
  3. невидимая запятая: ai⁣j
Изменение структуры

Вы можете изменить структуру существующего выражения, например добавление надстрочного индекса, заключение выражения в круглые скобки или поворот выражение в числителе дроби. Для этого выберите выражение и введите новую конструкцию с Math палитра, подменю Insert/Math или клавиатуру.

Вы также можете использовать Преобразование из Инструменты меню. Выберите выражение, которое хотите преобразовать, и Transform отобразит меню со всеми возможными изменениями. За конструкции, не являющиеся частью разметки Presentation MathML, т.е. только доступны из палитры — нажатие на кнопку поместит выбранный выражение в самом естественном заполнителе.

Изменение выражения полезно для сохранения рекурсивной структуры, даже если вы введите формулу линейно. Например, чтобы войти х2≤925⇒x≤35 можно,

  • либо ввести «рекурсивно» (быстрее, но менее естественно для длинных выражений) :
    • ⇒
      • .
    • ≤⇒
    • ≤⇒
    • х≤⇒
    • x2≤⇒
    • x2≤⇒
    • x2≤9⇒
    • …
  • или вводите «линейно» (пишете как читаете, но нужно подбирать несколько раз) :
    • х
    • х
    • x2
    • x2≤
    • x2≤9
    • x2≤9
    • . ..

Обычно используются оба метода.

Просмотр структуры в MathML

Структуру MathML в документе можно просмотреть, выбрав Показать Структура из меню Views . Выбор этого варианта открывает представление «Структура», которое показывает основную структуру документа, математические элементы и их содержимое.

Математические выражения можно редактировать в основном виде или в виде структуры.

Представление структуры особенно полезно для избежания двусмысленности. Например, в уравнение ниже, поместив курсор после символа б, неясно, хотите ли вы что-то добавить в квадрате корень или после него.

x=a+b+1

Выбор (или проверка) в представлении структуры позволяет избежать ошибочного выбора. Ты также можно проверить строку состояния в нижней части окна.

Связывание в MathML

Вы можете создавать и использовать ссылки в математических выражениях. Эти ссылки представлен с помощью XML Linking Язык (XLink).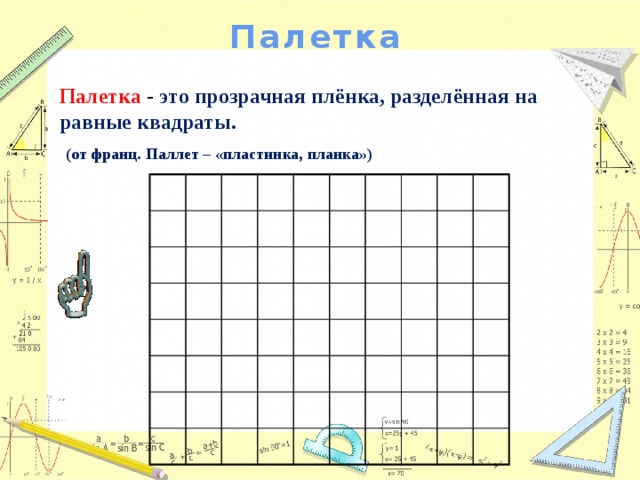 Только простые однонаправленные гиперссылки доступны в Amaya, но вы можете связать ссылку с любой частью формулы. Например, дробь в приведенной ниже формуле является ссылкой на домашнюю страницу W3C:

y=1×2+1

Двойной щелчок или щелчок правой кнопкой мыши по любому символу внутри дробной загрузки Домашняя страница W3C.

Чтобы создать такую ​​ссылку, выберите математическое выражение (дробь в приведенном выше например, нажав на дробную полосу), нажмите кнопку в инструменте Elements или выберите Создать или изменить ссылку из меню Ссылки , и щелкните нужную цель.

Если целью является выражение в формуле, необходимо сначала включить выражение в цель. Выберите выражение и выберите Создать target из меню Links для создания Атрибут id для целевого выражения.

Подробнее о MathML

Совместимость с браузерами

Некоторые браузеры поддерживают MathML:

  • Internet Explorer с подключаемым модулем MathPlayer
  • Firefox и другие браузеры на базе Gecko
  • Opera начиная с версии 9. 5

Необходимо использовать суффикс .xml , чтобы убедиться, что XHTML документы управляются как XML. Без этого суффикса некоторые браузеры не отображают правильно документировать, содержащие математические выражения. Это также рекомендуется использовать utf-8 кодировка для всех документов XML.

По умолчанию Amaya добавляет тип документа XHTML 1.1 плюс MathML 2.0 в начало документа. Этот тип документа не является обязательным, но полезен:

  • для проверки документа,
  • для создания буквенно-цифровых объектов (таких как ∫) для математических символов в исходном коде. В противном случае математические символы кодируются как любой другой символ Юникода.

К сожалению, этот тип документа не поддерживается многими браузерами. Так что это могло необходимо удалить этот тип документа с помощью команды Amaya: Инструменты/Изменить тип документа/Удалить тип документа .

IE использует таблицу стилей преобразования pmathml. xsl и подключаемый модуль для отображения кода MathML, включенного в документы XHTML. Амайя добавляет автоматически ссылка на эту таблицу стилей преобразования, но автор должен сохраните копию этой таблицы стилей (pmathml.xsl) в локальном каталог документа.

Известные проблемы
  • Amaya реализует только презентационную часть MathML 2.0, а не Часть разметки контента.
  • Некоторые теги презентации не полностью доступны: mglyph , действие
  • Доступны все элементы и атрибуты презентации, но только на экран выводятся следующие атрибуты: display, alttext, mathvariant, mathsize, mathcolor, mathbackground, размер шрифта, вес шрифта, стиль шрифта, семейство шрифтов, цвет, толщина линии, numalign, denomalign, скошенный, обозначение, lquote, rquote, lspace, rspace, largeop, movablelimits, subscriptshift, superscriptshift, форма, ширина (только mspace), высота (только mspace), глубина (только mspace), выравнивание, выравнивание строк, выравнивание столбцов, фрейм, интервал между кадрами, стиль отображения, сторона, rowspan, columnspan, rowspan, columnspace, rowlines, столбцы .
  • Класс , id и Доступны атрибуты стиля с той же семантикой, что и в (X)HTML: вы можете связать стили CSS с элементами MathML ( класс и 9атрибуты 0044 стиля ) и элемент MathML может быть целью ссылки (атрибут id ).
  • Amaya использует шрифты STIX для отображения математических символов, но в настоящее время поддерживаются не все символы.

Расширение математической палитры для формирования модели развития: пегий

. 2019 май;81(5):1461-1478.

doi: 10.1007/s11538-019-00569-1. Эпаб 201928 января.

Микаэль Дугу 1 , Кристиан Мацца 1 , Бит Шваллер 2 , Ласло Пече 3

Принадлежности

  • 1 Факультет математики, Университет Фрибурга, Chemin du Musée 23, 17:00, Фрибур, Швейцария.
  • 2 Анатомия, отделение медицины, Университет Фрибурга, Route Albert-Gockel 1, 1700, Фрибург, Швейцария.
  • 3 Анатомия, отделение медицины, Университет Фрибурга, Route Albert-Gockel 1, 1700, Фрибург, Швейцария. [email protected].
  • PMID: 30689102
  • DOI: 10.1007/с11538-019-00569-1

Майкл Дугу и др. Бык Математика Биол. 2019 май.

. 2019 май;81(5):1461-1478.

doi: 10.1007/s11538-019-00569-1. Epub 2019 28 января.

Авторы

Микаэль Дугу 1 , Кристиан Мацца 1 , Бит Шваллер 2 , Ласло Пече 3

Принадлежности

  • 1 Факультет математики, Университет Фрибурга, Chemin du Musée 23, 17:00, Фрибур, Швейцария.
  • 2 Анатомия, отделение медицины, Университет Фрибурга, Route Albert-Gockel 1, 1700, Фрибург, Швейцария.
  • 3 Анатомия, отделение медицины, Университет Фрибурга, Route Albert-Gockel 1, 1700, Фрибург, Швейцария. [email protected].
  • PMID: 30689102
  • DOI: 10. 1007/с11538-019-00569-1

Абстрактный

Здесь мы представляем теоретическое исследование с потенциальным пониманием механизмов развития. Три биологических фактора, состоящие из двух факторов диффузии и клеточно-автономного неподвижного фактора транскрипции, сочетаются с различными механизмами обратной связи. Это приводит к четырем различным ситуациям или рисункам меха. Два из них воспроизводят классические тьюринговские паттерны: (1) регулярно расположенные пятна, (2) лабиринтные паттерны или прямые линии с начальным наклоном при активации транскрипционного фактора. Третья ситуация не приводит к шаблонам, но приводит к различным однородным цветовым тонам. Наконец, четвертый проливает новый свет на возможные механизмы, ведущие к образованию пегих рисунков, примерами которых служат случайные узоры на шерсти некоторых пород коров и далматинских собак. Пьебалдизм обычно проявляется в виде белых участков меха, волос или кожи из-за отсутствия клеток, вырабатывающих пигмент, в этих областях. Распределение белых и цветных зон не отражает классические закономерности Тьюринга. Мы показываем, что эти пегие паттерны носят преходящий характер, развиваясь из случайных начальных условий и полагаясь на бистабильность системы. Численно показано, что наличие клеточно-автономного фактора не только расширяет диапазон параметров диффузии реакции, в котором может возникнуть паттерн, но и расширяет паттернообразующие способности уравнений реакции-диффузии.

Ключевые слова: пьебалдизм; Развитие рисунка кожи; Узор Тьюринга.

Похожие статьи

  • Клетки линии меланоцитов в пегой коже.

    Хаттори М., Симидзу А., Исида-Ямамото А., Вакамацу К., Исикава О. Хаттори М. и др. J Дерматол. 2019 сен; 46 (9): 816-818. дои: 10.1111/1346-8138.14999. Эпаб 201928 июня. J Дерматол. 2019. PMID: 31254302 Аннотация недоступна.

  • Двухэтапная модель Тьюринга для создания пигментных рисунков на леопарде и ягуаре.

    Liu RT, Liaw SS, Maini PK. Лю Р.Т. и др. Phys Rev E Stat Nonlin Soft Matter Phys. 2006 г., июль; 74 (1 часть 1): 011914. doi: 10.1103/PhysRevE.74.011914. Epub 2006 21 июля. Phys Rev E Stat Nonlin Soft Matter Phys. 2006. PMID: 16

    4

  • Математически управляемые подходы к различению моделей периодического формирования паттернов.

    Hiscock TW, Megason SG. Хискок Т.В. и соавт. Разработка. 2015 1 февраля; 142 (3): 409-19. дои: 10.1242/dev.107441. Разработка. 2015. PMID: 25605777 Бесплатная статья ЧВК. Обзор.

  • Чувствительность самоорганизации Тьюринга к задержкам биологической обратной связи: 2D-модели пигментации рыб.

    Гаффни Э.А., Ли С.С. Гаффни Э.А. и соавт. Математика Мед Биол. 2015 март; 32(1):56-78. doi: 10.1093/imammb/dqt017. Epub 2013 1 октября. Математика Мед Биол. 2015. PMID: 24087834

  • Пьебалдизм, синдром Ваарденбурга и связанные с ним нарушения развития меланоцитов.

    Spritz РА. Спритц РА. Семин Кутан Мед Хирург. 1997 март; 16(1):15-23. doi: 10.1016/s1085-5629(97)80031-4. Семин Кутан Мед Хирург. 1997. PMID: 9125761 Обзор.

    • Посмотреть все похожие статьи

    термины MeSH

    6

    Справка по палитре ответов

    Справка по палитре ответов

    Справка по палитре ответов

    Кнопки Зона

    Область кнопок предоставляет учащемуся с различными инструментами для создания, изменения и сброса
    своего ответа в Ответе Поле. Кнопка справки также доступна для отображения обзора функции и функции
    для студенческого представления палитры ответов.

    Область кнопок можно разбить на три категории: кнопки объекта, кнопки действий,
    и кнопка справки. Эти категории описаны ниже.

    Кнопка Тип Кнопка Описание
    Объект Кнопки

    Кнопки объектов позволяют учащемуся способность отвечать на математические вопросы, требующие более простой текстовый ответ. Для ответов на некоторые вопросы может потребоваться дроби, радикалы, показатели степени и т. д., и без доступного Объекта кнопки, учащимся будет трудно сформулировать последовательную форматированный ответ.

    Есть множество объектов Кнопки, которые вставляют математический элемент определенного типа в ответ Поле. Каждая кнопка объекта может иметь одно или несколько редактируемых полей. для заполнения студентом.

    Мощность

    		 Корень Фракция-й корень

    Научная
    Обозначение


    Интеграл

    		 Ограничение Скобка Пи

    Плюс/Минус

    		 Индекс

    Бесконечность

    		 Умножение

    Стрелка вправо

    		 Меньше
    или равно    		 Больше
    или равно    		 супер и
    индекс

    Вектор Валентность 1 Льюис
    Электрон    		 2 Льюис
    Электроны

    Помощь Кнопка Кнопка справки покажет обзор функций и функций, которые студент Просмотр математической палитры может предложить.
    Кнопка справки

     

     

    Поле ответа

    Поле ответа принадлежит учащемуся. рабочая зона для построения своего ответа на 9 математических палитр0052 соответствующий вопрос. Ответ может состоять из простого текста, объекта из области кнопок,
    или любой их комбинации.

    В зависимости от типа вопроса с которой связана палитра ответов, существует два разных состояния
    , в которых может находиться поле ответа.  Эти «состояния по умолчанию» описаны ниже:

    Ответ Тип состояния поля Описание
    Пусто

    Если поле ответа пусто, учащийся может вставлять любую комбинацию объектов из области кнопок и/или обычный текст, когда они строят свой ответ.

    Leave a Comment on Математическая палетка: Палетка для математики (3 класс): как сделать и как пользоваться?Разное

    About the Author

    admin

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    Related Posts

    © 2024 Воронежская благотворительная организация «Общие дети»