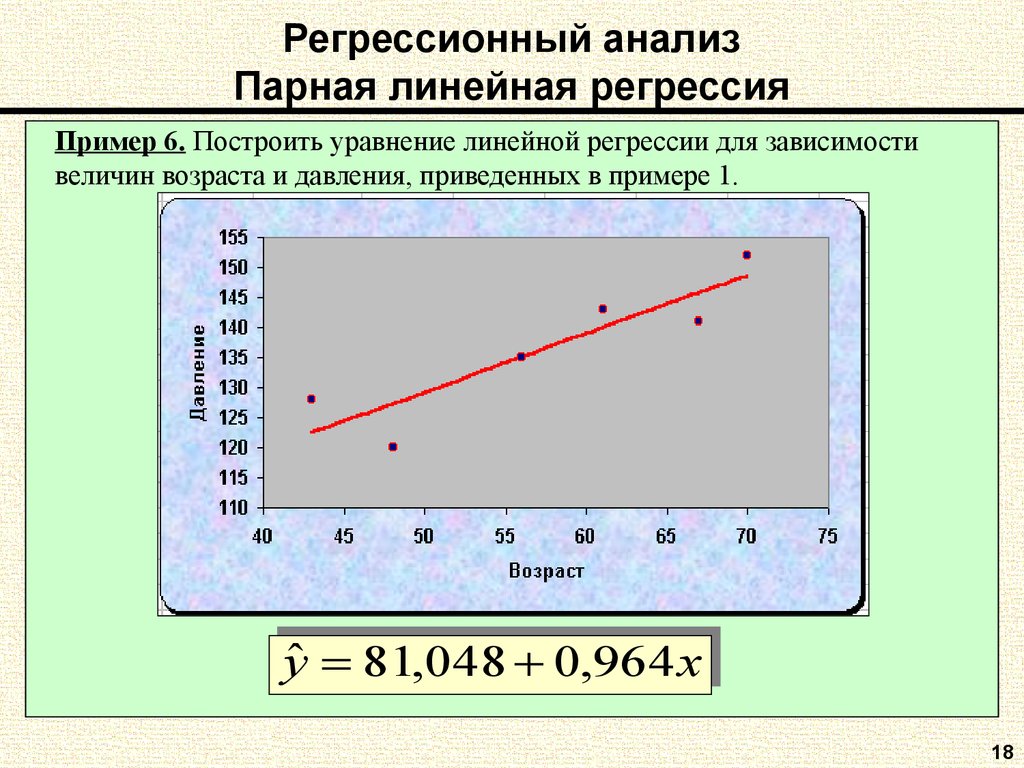
Методы регрессии — CoderLessons.com
Регрессия – это статистический метод, который помогает квалифицировать отношения между взаимосвязанными экономическими переменными. Первый шаг включает в себя оценку коэффициента независимой переменной, а затем измерение достоверности оцененного коэффициента. Это требует формулирования гипотезы, и на основе гипотезы мы можем создать функцию.
Если менеджер хочет определить взаимосвязь между рекламными расходами фирмы и доходами от продаж, он подвергнется проверке гипотезы. Предполагая, что более высокие расходы на рекламу приводят к увеличению продаж для фирмы. Менеджер собирает данные о расходах на рекламу и о выручке от продаж за определенный период времени. Эта гипотеза может быть переведена в математическую функцию, где она приводит к –
Y = A + Bx
Где Y – продажи, x – расходы на рекламу, A и B – постоянные.
После перевода гипотезы в функцию основание для этого должно найти связь между зависимой и независимой переменными.
Значение зависимой переменной имеет наибольшее значение для исследователей и зависит от значения других переменных. Независимая переменная используется для объяснения изменения зависимой переменной. Это может быть классифицировано в два типа –
Простая регрессия – одна независимая переменная
Множественная регрессия – несколько независимых переменных
Простая регрессия
Ниже приведены шаги для построения регрессионного анализа –
- Укажите модель регрессии
- Получить данные о переменных
- Оценить количественные отношения
- Проверьте статистическую значимость результатов
- Использование результатов в принятии решений
Формула для простой регрессии –
Y = a + bX + u
Y = зависимая переменная
X = независимая переменная
а = перехват
б = уклон
и = случайный фактор
Данные поперечного сечения предоставляют информацию о группе объектов в данный момент времени, тогда как данные временных рядов предоставляют информацию об одном объекте с течением времени.
Когда мы оцениваем уравнение регрессии, оно включает в себя процесс определения наилучшей линейной зависимости между зависимой и независимой переменными.
Метод обыкновенных наименьших квадратов (OLS)
Обычный метод наименьших квадратов предназначен для подгонки линии через разброс точек таким образом, чтобы сумма квадратов отклонений точек от линии сводилась к минимуму. Это статистический метод. Обычно программные пакеты выполняют оценку OLS.
Y = a + bX
Коэффициент определения (R
2 )Коэффициент детерминации – это мера, которая показывает процент изменения зависимой переменной из-за изменений в независимых переменных. R 2 является показателем качества модели соответствия. Ниже приведены методы –
Общая сумма квадратов (TSS)
Сумма квадратов отклонений значений выборки Y от среднего значения Y.
TSS = SUM (Y i – Y) 2
Y i = зависимые переменные
Y = среднее значение зависимых переменных
я = количество наблюдений
Регрессия Сумма квадратов (RSS)
Сумма квадратов отклонений расчетных значений Y от среднего значения Y.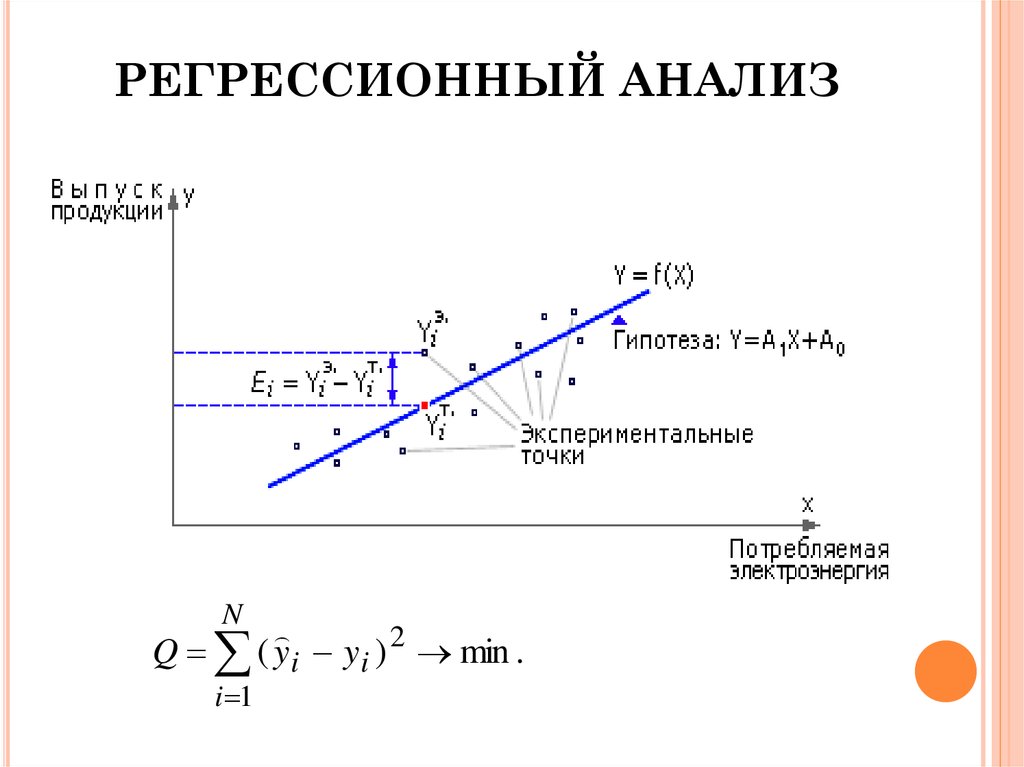
RSS = СУММА (Ỷ i – uY) 2
Ỷ i = оценочное значение Y
Y = среднее значение зависимых переменных
я = количество вариантов
Ошибка суммы квадратов (ESS)
Сумма квадратов отклонений выборочных значений Y от расчетных значений Y.
ESS = СУММА (Y i – Ỷ i ) 2
Ỷ i = оценочное значение Y
Y i = зависимые переменные
я = количество наблюдений
R2 =
RSS / TSS
= 1 –
ESS / TSS
R 2 измеряет долю общего отклонения Y от его среднего значения, что объясняется регрессионной моделью. Чем ближе R 2 к единице, тем больше объясняющая сила уравнения регрессии. Значение R 2, близкое к 0, указывает на то, что уравнение регрессии будет иметь очень мало объяснительной силы.
Для оценки коэффициентов регрессии используется выборка из совокупности, а не всей совокупности.
Оценка коэффициентов регрессии
Каждая выборка из населения генерирует свой собственный перехват. Для расчета статистической разницы можно использовать следующие методы:
Двуххвостый тест –
Нулевая гипотеза: H 0 : b = 0
Альтернативная гипотеза: H a : b ≠ 0
Один хвостатый тест –
Нулевая гипотеза: H 0 : b> 0 (или b <0)
Альтернативная гипотеза: H a : b <0 (или b> 0)
Статистический тест –
т =
(b – E (b)) / SE b
б = расчетный коэффициент
E (b) = b = 0 (нулевая гипотеза)
SE b = стандартная ошибка коэффициента
,
Значение t зависит от степени свободы, одного или двух неудачных испытаний и уровня значимости.
Множественный регрессионный анализ
В отличие от простой регрессии в множественном регрессионном анализе, коэффициенты указывают на изменение зависимых переменных, предполагая, что значения других переменных постоянны.
Тест статистической значимости называется F-тестом . F-тест полезен, поскольку он измеряет статистическую значимость всего уравнения регрессии, а не только для отдельного человека. Здесь В нулевой гипотезе нет никакой связи между зависимой переменной и независимыми переменными совокупности.
Формула – H 0 : b1 = b2 = b3 =…. = bk = 0
Не существует никакой связи между зависимой переменной и k независимыми переменными для совокупности.
F-тест статический –
F= frac left( fracR2K right) frac(1−R2)(nk−1)
Критическое значение F зависит от числителя и знаменателя, степени свободы и уровня значимости. F-таблица может быть использована для определения критического значения F. По сравнению с F – значением с критическим значением (F *) –
Если F> F *, нам нужно отвергнуть нулевую гипотезу.
Если F <F *, не отклоняйте нулевую гипотезу, так как нет существенной связи между зависимой переменной и всеми независимыми переменными.
Регрессия – что это такое простыми словами
Содержание статьи:
- 1 Регрессия в психологии
- 2 Регрессия в математике
- 3 Регрессия в статистике
- 4 Морская регрессия
Часто в математике, экономике и других отраслях деятельности можно встретить такой термин, как «регрессия». В переводе с латинского это слово означает «отступление», «возвращение».
В зависимости от контекста регрессия означает немного разные явления, однако есть общее сходство – практически всегда имеется в виду переход от прогресса в обратную сторону.
Это спуск вниз, с верхней ступени развития к нижней.
Регрессия в психологии
В психоанализе применяется термин «регрессия», где таким образом маркируют возврат от более высокой ступени психологической организации к низкой. Например, в ходе психоаналитической сессии пациент может вернуться к предыдущим этапам своего эмоционального, сексуального развития, к более примитивным и упрощенным вариантам поведения, мышления, реагирования.
Регрессией называют и сам процесс движения психики пациента в новый формат. Иногда регрессия необходима как один из этапов преодоления комплексов, зависимости, раскрытия причин психотравм и душевных ран. Это необходимо для адаптации человека к переменам во внутреннем мире и внешней среде.
Психологическая регрессия
Наблюдается также регрессия поведения – это одна из форм защиты, когда человек внутренне уходит от реальности и неблагоприятных событий в действительности.
Это временный, как правило, переходный вариант поведения, необходимый для адаптации. Так работает универсальный механизм встроенной защиты.
Это временный, как правило, переходный вариант поведения, необходимый для адаптации. Так работает универсальный механизм встроенной защиты. Человек возвращается на прошедшую стадию развития, чтобы облегчить собственное состояние, перенести разные по силе переживания.
Регрессия в математике
В математических науках регрессия применяется как относительная величина, отражающая зависимость среднего показателя
какой-то величины от другой или нескольких величин. Такой может быть «множественная регрессия».Линейной регрессией называют статистическую модель, отражающую зависимость одной переменной у от различных факторов – одного или нескольких. Такие факторы – независимые переменные – называются регрессорами. Через линейную регрессию можно восстановить зависимость между двумя любыми переменными.
Существует также криволинейная регрессия, где в уравнении прописываются изменения одной переменной у в качестве функции t для изменения в другой переменной – х. Это квадратное уравнение, бывает также кубическое или уравнение другого, более высокого порядка. В криволинейной регрессии отсутствуют постоянные коэффициенты, отражающие изменения между переменными.
В математических расчетах также применяются другие типы регрессий: одномерная, полиномиальная, логистическая, множественная.
Логистическая регрессия рассматривает случаи связей между разными двумя классами, позволяет вывести обоснования и минимизировать эмпирический риск. Этот метод применяется в так называемой байесовской классификации, в методах настройки весов.
При помощи логистической регрессии (она же логит-регрессия, логит-модель) предсказывают степень вероятности наступления разных событий. Результат подгоняется к логистической кривой с использованием полученных модельных данных.
Регрессия в статистике
Для точности результатов в статистике важна корректная постановка задачи – таким путем можно правильно восстановить структуру логит-модели. Выработка правильного алгоритма обеспечит отыскание правильных параметров.
В статистике применяется линейный дискриминант Фишера на основе логистической регрессии. Он основан на байесовских правилах (байесовская сеть). Применяется принцип максимального правдоподобия, но на практике достигаются очень разные результаты.
Другой метод математической статистики – множественная регрессия, которая является расширенной версией простого варианта регрессии. Этот метод позволяет прогнозировать действия одной переменной или ее критериев (измерения переменной).
Множественная регрессия используется для многомерного анализа, где наблюдаются взаимосвязи между зависимой переменной у и совокупности предикторов – независимых переменных х, расчет делается на базе линейного уравнения.
В виде регрессии обычно также представлен исходный код в основе компьютерной программы.
Морская регрессия
Так называемая «морская регрессия» характеризует период отлива – регулярного, обусловленного положением Луны на орбите, когда морские воды отступают от берегов.
Суша поднимается, опускается океаническое дно и в случае тектонических разломов, землетрясений.
В прошедшие эпохи геологические изменения регрессивного характера затрагивали целые материки – сокращался объем воды в океанах, менялись очертания берегов в ледниковый период.
Чаще всего регрессия моря – это уменьшение количества воды в Мировом океане в целом (как следствие массивного оледенения материков). При этом опускаются большие участки морского или океанического ложа, уровень и количество воды существенно падает.
Поделитесь статьёй в социальных сетях:
Что такое регрессионный анализ? » Учебники по экономике
В эконометрике мы используем инструмент регрессионного анализа, чтобы понять экономические отношения посредством количественной оценки. Эта количественная оценка выполняется с помощью регрессии, которая является одним из наиболее частых и важных инструментов, используемых для понимания экономических теорий. Следовательно, легко описать зависимость в теоретической форме, но было бы трудно записать ее в виде уравнения и оценить теорию по заданным данным. Кроме того, мы находим не только взаимосвязь переменных, но и направление и величину изменения переменных, используемых в теории. Таким образом, чтобы предсказать оба фактора: 1) количество изменений 2) направление изменений, а также значимость взаимосвязи между переменными, мы используем регрессионный анализ.
Определение регрессионного анализа
Регрессионный анализ — это статистический метод, который фактически объясняет изменение зависимой переменной вследствие движения других независимых переменных.
Это метод предсказания неизвестной переменной через известные переменные.
Зависимая переменная, независимая переменная и причинно-следственная связь в регрессионном анализе:
Зависимая переменная — это переменная, которая зависит от действия независимой переменной. Любые изменения, сделанные в независимой переменной, приведут к изменению зависимой переменной. Это причинно-следственная связь между переменными.
Важный момент: Другие имена зависимой и независимой переменной.
Зависимая переменная = Независимая переменная = Регрессия
Независимая переменная = Переменная-причина = Регрессор
Чтобы понять взаимосвязь зависимой и независимой переменных в регрессионном анализе: Поясним это на примере:
Q=ƒ(P,Ps,Yd)
Где Q есть величина спроса и зависимая переменная, на которую влияет независимая переменная P= Цена, Ps= Цена заменителей и Yd= Доход
Это уравнение объясняет, что объем спроса является функцией всех этих переменных.
Любое изменение этих переменных изменит требуемое количество (при сохранении других параметров постоянными).
Причина использования слова «сохранение других вещей постоянными» заключается в том, что мы не сможем понять влияние одной независимой переменной на независимую переменную, если все переменные и их влияние проверяются одновременно. Вот почему мы оцениваем переменную таким образом, чтобы другие вещи оставались постоянными при анализе влияния одной переменной на зависимую переменную.
Обратите внимание, что большая часть эконометрического анализа связана с причинно-следственными связями. Тем не менее, вы должны помнить, что регрессионный анализ заключается не только в доказательстве связи между случаем и следствием. это скорее понимание силы и направления эффекта при условии, что переменная действительно имеет значимую связь или нет.
Простая регрессионная модель
Простая регрессионная модель представляет собой линейную модель с одним уравнением, которую можно объяснить следующим образом:
Y=β* + β¹X
Приведенные выше уравнения утверждают, что Y является зависимой переменной и представляет собой линейную функцию одного уравнения от независимой переменной X.
Почему мы называем это линейным?
Модель является линейной по следующим причинам:
- Если мы построим уравнения, это будет прямая линия.
- Это простое линейное уравнение с одной переменной, поскольку оно включает только один коэффициент переменной β1 . Это будет многомерная регрессионная модель, если она включает более одного коэффициента переменной.
- Это будет не кривая, а прямая линия, а прямая линия показывает постоянный наклон или скорость изменения в каждой точке.
- Коэффициент наклона показывает, что Y изменится, когда X увеличится на одну единицу.
График простой линейной регрессии
Источник: Studenmund, Книга по эконометрике, глава 2, Простой регрессионный анализ .
Также обратите внимание, что в регрессионном анализе упор делается больше на коэффициенты наклона, такие как β1. В приведенной выше прямолинейной регрессии наклон постоянен на протяжении всей функции. а постоянный наклон означает, что изменение X на одну единицу приведет к такому же изменению Y.
Всякий раз, когда вы запускаете регрессию в любом программном обеспечении, суть всего уравнения заключается в том, что оно должно быть линейным. И если это не линейно, то вы должны сделать его линейным, прежде чем запускать регрессионный анализ.
Линейное уравнение против нелинейного уравнения
Линейное уравнение:
Y= β 0 +β 1 X
где :
3
Нелинейное уравнение может выглядеть примерно так:
Y= β 0 +β 1 X 2
Приведенное выше уравнение является нелинейным, а скорее квадратным уравнением, по которому мы можем провести регрессию в любом доступном программном обеспечении. Чтобы упростить нам выполнение регрессионного анализа, мы сначала попытаемся сделать уравнение линейным.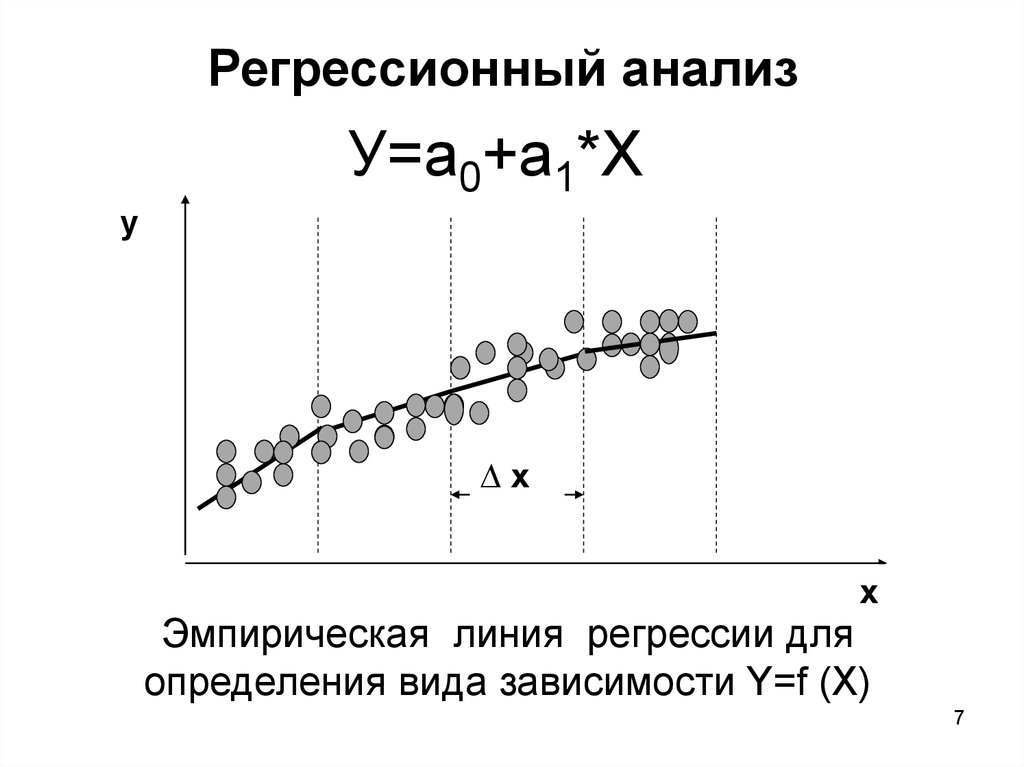
Для этого мы создаем новую переменную, которая равна квадрату X.
Z=X 2
Теперь уравнение принимает следующий вид:
Уравнение теперь можно оценить с помощью регрессионного анализа, так как оно имеет линейную форму.
страница не найдена — Колледж Уильямс
| ’62 Центр театра и танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий/помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр изучения карьеры, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Приемная, Weston Hall | 597-2211 | 597-4052 факс |
| Позитивные действия, Хопкинс-холл | 597-4376 | |
| Африканские исследования, Холландер | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Сойер | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art/Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Студия фотографии, Spencer Studio Art | 597-2030 | |
| Студия гравюры, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео/фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Голландия | 597-2391 | 597-3028 факс |
| Астрономия/астрофизика, Физика Томпсона | 597-2482 | 597-3200 факс |
| Отделение легкой атлетики, физического воспитания, отдыха, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочная пристань, озеро Онота | 443-9851 | |
| Вагоны | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Ледовая линия хоккейного катка, Lansing Chapman | 597-2433 | |
| Очные занятия, Спортивный центр Чендлера | 597-3321 | |
| Физкультура | 597-2141 | |
| Мокрая линия бассейна, Спортивный центр Чендлера | 597-2419 | |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Корты для сквоша | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Биология Томпсона | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Томпсон Биология | 597-2126 | 597-3495 факс |
| Безопасность и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа/Системы сигнализации | 597-4970/4033 | |
| Служба сопровождения, Хопкинс-холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Распределительный щит | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, выпуск 1966 г. About the Author Related Posts |