Образ Я, Я-концепция — Психологос
Фильм «Итальянский для начинающих»
Я-концепция — сложившееся представление человека о самом себе, как о человеке и личности.
Американский психолог У. Джеймс («Принципы психологии», 1890 г.) первым предложил идею Я-концепции и внес существенный вклад в ее разработку. Согласно Джеймсу, «глобальное Я» (личность) содержит в себе два аспекта: эмпирический объект (Ме), познаваемый субъективным оценивающим сознанием (I). Я как объект состоит из четырех аспектов: духовное Я, материальное Я, социальное Я и телесное Я, которые и образуют для каждого человека уникальный образ или совокупность представлений о себе как личности. Кроме этого, Джеймс предложил формулу оценивания личностью самого себя. Формула самооценки выражается в сравнении достигнутых успехов с уровнем притязаний:
самооценка = успехи/притязания
Фильм «Облачно, возможны осадки в виде фрикаделек»
Позже «я-концепция» разрабатывала в необихеворизме (теория социального научения А.
Из чего состоит Я-концепция
Есть понятие «внутренняя картина болезни» — то, как человек воспринимает свое заболевание. А «я-концепция» — внутренняя картина себя, то, что известно индивиду о самом себе, каким он видит, чувствует и представляет себя сам. Это
- Образ Я — представление человека о самом себе: о своем уме, теле, способностях, чертах характера
- Субъективное отношение человека к самому себе: принятие или нет, та или иная самооценка, высокое или не очень самоуважение
- Действия и реакции, которые человек считает «присущими ему», «достойными себя», выражающими его Я
Позитивная Я-концепция — это позитивное отношение к себе, самоуважение и принятие себя, ощущение собственной ценности. Негативная Я-концепция — негативное отношение к себе, неприятие себя, ощущение своей неполноценности.
Устойчивость и изменение Я-концепции
Я-концепция — обычно очень устойчивая конструкция. Представления человека о самом себе, как правило, кажутся ему убедительными независимо от того, основываются ли они на объективном знании или субъективном мнении, являются ли они истинными или ложными.
Это больше похоже на школьное сочинение, которое рождается часто случайно, неизвестно откуда, и при этом сочиняется под определенную задачу.
Несмотря на устойчивость, «я-концепция» — меняться может и меняется. На ее изменение обычно влияют:
- контакты со «значимыми другими».
Как ведут себя «значимые другие», обычно оказывается образцом или хотя бы ориентиром. Образ жизни родителей — впитывается ребенком.
То, что значимые люди о нас думают, как правило, сильно влияет на наши представления о себе и отношение к самому себе.
- общий эмоциональный фон.
Общий уровень эмоционального тона, ситуативное настроение, состояние здоровье и психосоматические обстоятельства.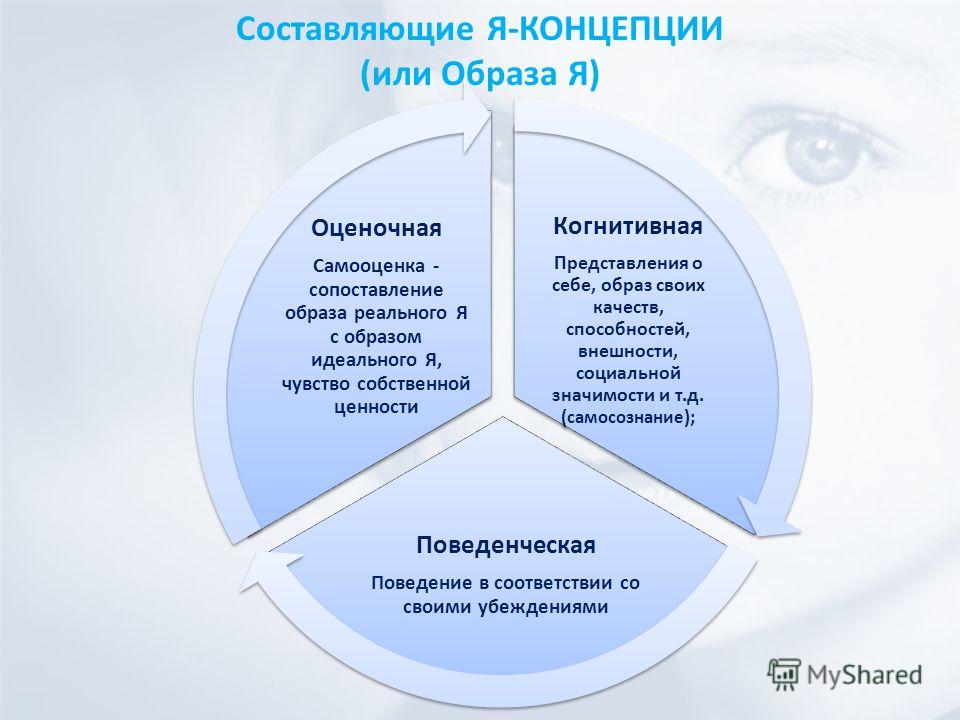
- сопоставление имеющегося и желаемого.
Например, сопоставление Я-реального и Я-идеального, сопоставление что я хотел сделать и что на самом деле не сделал.
- внутренние выгоды.
Самооценка во многом меняется не «потому что», а «для того, чтобы», в рамках тех или иных ситуативных или личностных выгод.
Я — образ – Мир Знаний
Психология
На протяжении своей жизни человек мало задумывается над единством и деталями своего «я», что, впрочем, не мешает ему всеми силами (большей частью подсознательными и бессознательными процессами) защищать целостность и сохранность данного образования.
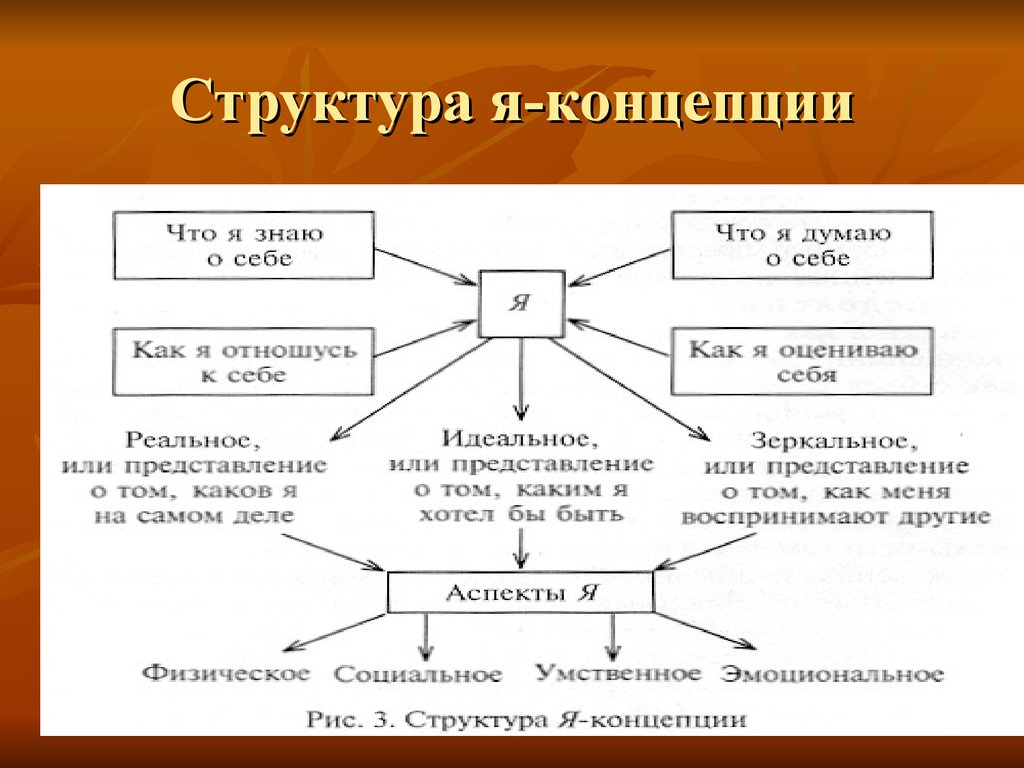
В попытках уточнить и как-то структурировать сложное понятие «я» ряд психологов выделили в нем ряд образований: «я»-образ, «я»-концепция, «эго». В научной психологии это впервые сделал У. Джеймс, разделив «я» на «я»-познающее и «я»-познаваемое. Бытуют и другие, во многом схожие между собой понятия: «я»-глубинное, «я»-реальное и «я»-идеальное, «я»-высшее и «я»-низшее, «я»-внутреннее и «я»-внешнее, «я»-потенциальное и «я»-актуальное. Уже сам перечень терминов наводит на мысль об отсутствии единого понимания этого вопроса.
Уже сам перечень терминов наводит на мысль об отсутствии единого понимания этого вопроса.
То, как индивид видит, представляет себе самого себя, свое поведение и свои внутренние переживания, можно объединить понятием «я»-образ», или «я»-концепция». «я»-образ — это попытка осознания себя как бы со стороны, и этим данное понятие отличается от целостного и гораздо более монолитного понятия «я». Надо понимать, что, выделяя понятие «я»-образа, психолог получает лишь отдаленное представление об истинных образованиях психики, отраженных в понятии «я».
В норме «я»-образ представляет целостное образование. Вместе с тем, имея достаточно четкие характеристики, «я»-образ не есть нечто законченное и неизменное, поскольку в разные периоды своей жизни, более того, если говорить точно, то в каждое мгновение, представление индивида о самом себе меняется. Иными словами, «я»-образ тесно привязан к временному параметру и временной динамике; вне временных рамок характеристика «я»-образа относительна.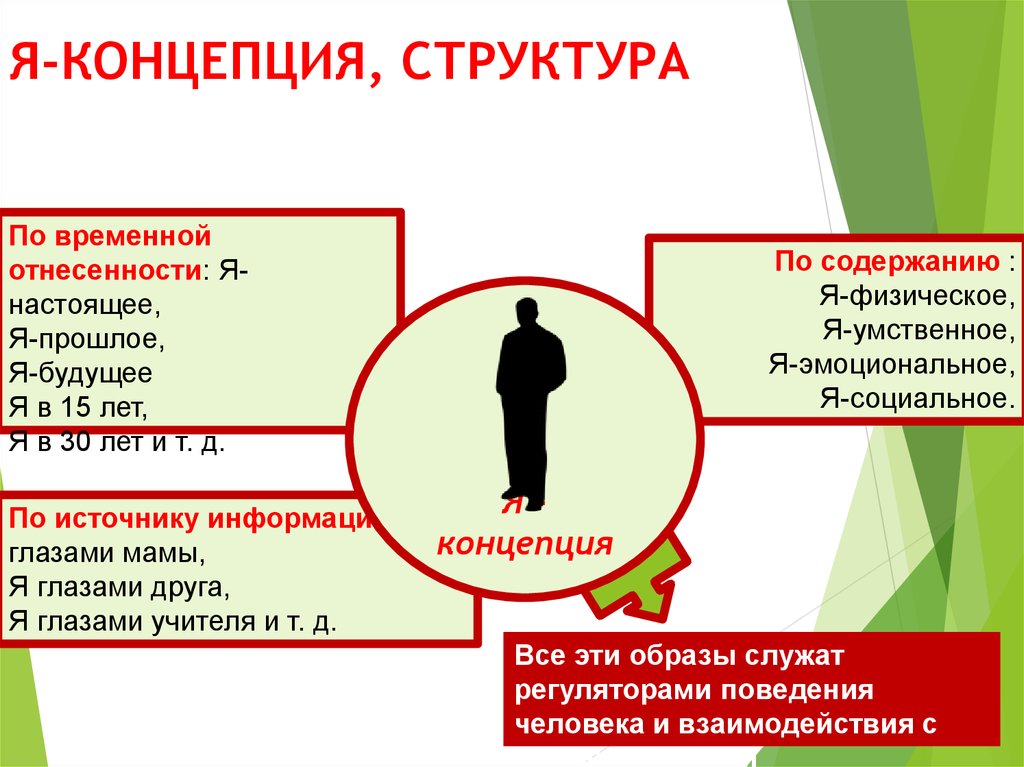
В переводной литературе нередко используется термин «я»-концепция», аналогичный «я»-образу». Это понятие прижилось, хотя представляется не самым удачным. Ведь понимание концепции изначально предполагает сколько-нибудь стройную и строгую систему взглядов, а самооценка себя — вещь достаточно переменчивая.
В «я»-образе можно выделить элементы «я»-реального и «я»-идеального. Под «я»-реальным понимается представление о самом себе, как сформированном, состоявшемся индивиде; под «я»-идеальным — то, к чему индивид стремится, каким ему хотелось бы видеть себя в идеале. «Я»-образ выступает как устоявшаяся система взглядов по отношению к самому себе, установка (см. ниже «Установка личности»), со всеми вытекающими позитивными и негативными последствиями. В рассматриваемом контексте «я»-образа более удачной (и логичной) видится модель «я»-актуального и «я»-потенциального (А.
По внешним признакам понятия «я»-актуального («я»-реального) и «эго» во многом схожи; действительно, представления о самом себе всегда в чем-то отражают «эго». Критерием различия служит факт контроля со стороны «эго». По форме больше всего подходит к «эго» понятие «я»-низшее — то, что заставляет окунаться в мир чувственных (материальных) наслаждений, забывая о внутреннем познании, и отворачивает от разбирательств самого себя.
Критерием различия служит факт контроля со стороны «эго». По форме больше всего подходит к «эго» понятие «я»-низшее — то, что заставляет окунаться в мир чувственных (материальных) наслаждений, забывая о внутреннем познании, и отворачивает от разбирательств самого себя.
Концепция изображений в обработке изображений
Воплотить этот проект в жизнь
Запустить градиент
Чтобы правильно понять процессы или концепции компьютерного зрения или обработки изображений в целом, необходимо понимать саму природу цифровых изображений. . В этой статье мы рассмотрим, что именно представляют собой изображения в цифровом пространстве, чтобы попытаться лучше понять и обработать их.
Оптическое и цифровое восприятие
В оптическом смысле, когда свет, отражающийся от объекта, попадает в человеческий глаз, в мозг посылаются сигналы, позволяющие нам воспринимать форму и цвет объекта. С другой стороны, в цифровой среде компьютер не способен воспринимать формы и цвета, а воспринимает изображение как набор чисел в пространственной плоскости.
Свойства цифровых изображений
Говоря об изображениях в цифровом контексте, на ум часто приходят три основных свойства. Это размерность, пиксель и канал. В этом разделе мы рассмотрим каждый из них.
Измерение
Измерение, также известное как координата или ось, представляет форму отсчета на пространственной плоскости (отсюда и термин пространственное измерение). Представьте себе плоский лист бумаги, поставленный на один из его краев лицом к вам. Представьте, что мы находимся в произвольной точке на этой плоскости, мы могли бы двигаться только вертикально (вверх и вниз), горизонтально (влево и вправо) или в какой-то комбинации из двух (под углом). Поскольку все ваши движения на этой плоскости можно суммировать, используя эти два направления, для того, чтобы перемещаться каким-либо осмысленным образом, нам потребуются две опорные линии, одна горизонтальная, называемая «x», а другая вертикальная, называемая «y», как показано ниже. Чтобы быть более точным, горизонтальную привязку можно назвать размером x, а вертикальную привязку размером y. Поскольку этих двух измерений достаточно, чтобы описать любое движение или фигуру на этом листе бумаги, мы можем сказать, что это двумерное (двухмерное) представление.
Поскольку этих двух измерений достаточно, чтобы описать любое движение или фигуру на этом листе бумаги, мы можем сказать, что это двумерное (двухмерное) представление.
А теперь представьте, если бы этот лист бумаги был лишь одной из шести поверхностей куба. Все это время мы двигались по этой поверхности, горизонтальный и вертикальный края поверхности представляют x и y соответственно. Так что, если мы хотим, например, попасть в центр куба, нам понадобится еще одна опорная линия, перпендикулярная (90 градусов) к поверхности, на которой мы сейчас находимся. Назовем этот размер опорной линии z. Внезапно мы теперь можем двигаться куда угодно внутри этого воображаемого куба, используя все 3 измерения, поэтому говорят, что куб является трехмерным (трехмерным) представлением.
Как мы упоминали ранее, все 3 опорные линии, которые мы упомянули, называются измерениями. Если у нас есть какие-то математические знания, мы обнаружим, что термины x, y и z являются контекстуально точными описаниями осей/размеров в декартовой системе координат (просто еще одно причудливое название трехмерной пространственной структуры). В более геометрическом смысле они назывались бы шириной, длиной и глубиной, в географии — долготой, широтой и высотой. Однако при обработке изображений (с использованием языка программирования Python) они называются размер/ось 1, размер/ось 0 и размер/ось 2 соответственно.
В более геометрическом смысле они назывались бы шириной, длиной и глубиной, в географии — долготой, широтой и высотой. Однако при обработке изображений (с использованием языка программирования Python) они называются размер/ось 1, размер/ось 0 и размер/ось 2 соответственно.
Измерения и номенклатура положений
Любая точка на пространственной плоскости может быть обнаружена путем обращения к ее положению во всех существующих измерениях. Рассмотрим точку k на двумерной плоскости в позиции (3, 5). Это означает, что точка расположена в 3 единицах от начала координат по оси x и в 5 единицах от начала координат по оси y. В целях номенклатуры точки в пространственной структуре называются (положение x, положение y), если они присутствуют в двумерном представлении, и (положение x, положение y, положение z), если они находятся на трехмерном изображении. представления Д.
Пиксели
Пиксели — это числовые представления, составляющие цифровое изображение. Их значения могут варьироваться от 0 (нет интенсивности) до 1 (максимальная интенсивность) при работе со значениями с плавающей запятой или от 0 (нет интенсивности) до 255 (максимальная интенсивность) при работе с целыми значениями. Эти пиксели объединяются, чтобы сформировать сетку (строки и столбцы) с размерами, упомянутыми в предыдущем разделе, чтобы сформировать 2-мерную фигуру.
Их значения могут варьироваться от 0 (нет интенсивности) до 1 (максимальная интенсивность) при работе со значениями с плавающей запятой или от 0 (нет интенсивности) до 255 (максимальная интенсивность) при работе с целыми значениями. Эти пиксели объединяются, чтобы сформировать сетку (строки и столбцы) с размерами, упомянутыми в предыдущем разделе, чтобы сформировать 2-мерную фигуру.
Рассмотрим двухмерную плоскость, которую мы использовали для иллюстрации в предыдущем разделе. Представьте, что оси закрыты, чтобы сформировать квадрат, как показано на изображении выше, тогда он по существу становится сеткой из 9столбцы и 9 строк. Когда эта сетка заполнена пикселями (обозначенными зелеными звездами только для удобства), она становится изображением из 9 строк на 9 столбцов, что означает, что имеется 9 столбцов и 9 рядов пикселей. Говоря более кратко, это становится (9, 9) пиксельным изображением. Чтобы определить общее количество пикселей, присутствующих в этом изображении, мы просто умножаем количество единиц, присутствующих в обоих измерениях, в данном случае 9*9 = 81 пиксель.
Пиксели и номенклатура позиций
В контексте обработки изображений с использованием языка программирования Python будет небольшая модификация двумерной плоскости, с которой мы работали. Во-первых, начало плоскости теперь должно располагаться в левом верхнем углу, а не в левом нижнем углу. Во-вторых, ось-y переименовывается в измерение-0/ось-0, а ось-x переименовывается в измерение-1/ось-1. Наконец, нумерация начинается с 0, то есть первый такт после начала координат равен 0 вместо 1.
После внесения всех этих изменений у нас теперь есть стандартный массив Python. Номенклатура пикселей в этом изображении в основном представляет собой индекс элементов в массиве. Пиксель в правом верхнем углу расположен с индексом [0, 8] , поскольку он расположен в первой строке (строка 0) и девятом столбце (столбец 8). В том же флюгере пиксели в пятой строке индексируются как [4] (строка 4). Любой пиксель изображения может быть расположен с помощью индексации массива в виде [номер строки, номер столбца] .
Создание простых изображений
В математике существует математическая формулировка, состоящая из строк и столбцов, эта формулировка называется матрицей. Как и в образце (9, 9) выше, матрица заполняется строками и столбцами числовых типов. В Python матрица может быть создана как массив с помощью библиотеки NumPy, поэтому разумно говорить, что цифровое изображение воспринимается компьютером как массив пикселей.
Чтобы доказать это, мы могли бы просто создать (9, 9) массив нулей и попытайтесь визуализировать его, как показано ниже. Как мы видим, поскольку все элементы (пиксели) в массиве равны 0 (нет интенсивности), при визуализации массив выглядит как затемненное изображение. Разрешить пока использование параметра ‘cmap’ в методе imshow(), это станет яснее позже.
# импортировать эти зависимости импортировать numpy как np import matplotlib.pyplot as plt
# создание (9, 9) массива нулей изображение = np.zeros ((9, 9)) # пытаемся визуализировать массив plt.Изображение создается при визуализации массива.imshow(изображение, cmap='серый')
Что произойдет, если не все элементы массива равны нулю? Помните в предыдущих разделах, где упоминалось, что при работе с целыми числами значения пикселей могут варьироваться от 0 (нет интенсивности) до 255 (максимальная интенсивность). Таким образом, теоретически, если мы создадим массив, заполненный диапазоном постепенно увеличивающихся целочисленных значений, мы должны получить изображение, в котором пиксели становятся все ярче. Давайте посмотрим, так ли это на практике.
# создание одномерного массива (вектора) элементов в диапазоне от 0 до 80 изображение = np.arange(81) # преобразование вектора в двумерный массив изображение = изображение.изменить((9, 9)) # пытаемся визуализировать массив plt.imshow(image, cmap='grey')Пиксели постепенно становятся ярче.
В приведенном выше кодовом блоке создается «одномерный массив» (фактически называемый вектором) с элементами в диапазоне от 0 до 80 (всего 81 элемент).
изображение
массив([[ 0, 1, 2, 3, 4, 5, 6, 7, 8],
[9, 10, 11, 12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23, 24, 25, 26],
[27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44],
[45, 46, 47, 48, 49, 50, 51, 52, 53],
[54, 55, 56, 57, 58, 59, 60, 61, 62],
[63, 64, 65, 66, 67, 68, 69, 70, 71],
[72, 73, 74, 75, 76, 77, 78, 79, 80]]) Массив, созданный с использованием приведенного выше блока кода.Дисперсия и относительная интенсивность пикселей
При работе с пикселями изображения интенсивность или яркость каждого пикселя зависит от общей природы всех пикселей. Другими словами, должны быть разные значения пикселей, чтобы интенсивность вступила в игру. Например, массив со всеми элементами со значением 100 будет отображаться как затемненное изображение (аналогично массиву нулей), поскольку дисперсия его элементов равна 0.
Например, массив со всеми элементами со значением 100 будет отображаться как затемненное изображение (аналогично массиву нулей), поскольку дисперсия его элементов равна 0.
Кроме того, при работе с целочисленными значениями пикселей, если все пиксели находятся в диапазоне от 0 до 10, яркость пикселей будет прогрессивно масштабироваться между этими значениями, при этом 0 соответствует самому темному, 10 — максимальной яркости и 5 — 5/11 яркости. максимальная яркость. Однако, если значения находятся в диапазоне от 1 до 100, пиксели со значением 1 будут казаться самыми тусклыми, пиксели со значением 100 — самыми яркими, а пиксели со значением 10 будут иметь яркость 1/10 от максимальной.
Создание осмысленных изображений
Становится все яснее, что, соединяя пиксели разной интенсивности, можно получить желаемую фигуру. По-прежнему используя наш (9, 9) пиксельный «холст», давайте попробуем создать массив, показанный ниже.
Этот массив состоит из набора нулей и единиц, причем единицы, по-видимому, выделяют контур буквы «J».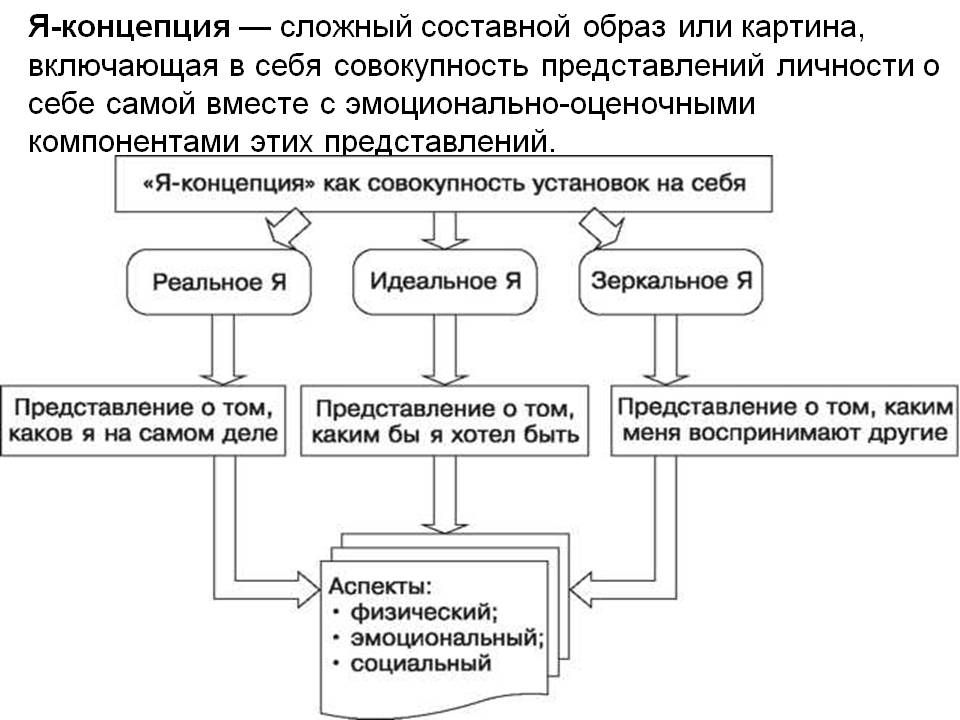 Основываясь на наших знаниях об интенсивности пикселей, мы знаем, что «нулевые» пиксели не имеют интенсивности (нет яркости), поэтому они будут казаться черными; мы также знаем, что «один» пиксель будет иметь максимальную интенсивность — в данном случае максимальную интенсивность, поскольку 1 — это максимальное значение. Само собой разумеется, что этот массив будет давать фигуру буквы «J» при визуализации.
Основываясь на наших знаниях об интенсивности пикселей, мы знаем, что «нулевые» пиксели не имеют интенсивности (нет яркости), поэтому они будут казаться черными; мы также знаем, что «один» пиксель будет иметь максимальную интенсивность — в данном случае максимальную интенсивность, поскольку 1 — это максимальное значение. Само собой разумеется, что этот массив будет давать фигуру буквы «J» при визуализации.
# создание массива изображение = np.zeros ((9, 9)) изображение[1, 2:-2] = 1 изображение[1:-1, 4] = 1 изображение[-2, 2:4] = 1 plt.imshow(image)
Так что да, объединение пикселей с различной интенсивностью даст желаемые цифры, если делать это достаточно осознанно. Следующий вопрос теперь будет заключаться в том, можно ли объединять пиксели для формирования более сложных изображений, таких как, например, изображение человеческого лица? Ответ на этот вопрос – решительное да! Конечно, нам понадобится больше 81 пикселя, поскольку человеческое лицо содержит множество деталей, но мастерское объединение пикселей для формирования сложных и реалистичных изображений — это в основном то, чем занимаются генеративные модели, такие как автоэнкодеры, генеративно-состязательные сети и DALL-E.
Воплотить этот проект в жизнь
Запустить градиент
Основные операции с изображениями
С осознанием того, что изображения, по сути, являются массивами, появилась возможность манипулировать ими, просто взаимодействуя с их представлениями в виде массивов. Любая математическая операция, применимая к матрицам, применима и к цифровым изображениям. Точно так же любая операция, применимая к массивам Python, может применяться и к цифровым изображениям.
Одной из очень простых операций с массивами, которая оказывает существенное влияние на работу с изображениями, является индексирование и нарезка массива. Просто разрезая массивы, можно было повернуть изображение под прямым углом. Следующий код демонстрирует этот процесс.
поворот по умолчанию (путь_изображения, угол):
"""
Эта функция поворачивает изображения под прямым углом
по часовой стрелке.
"""
если угол % 90 != 0:
print('может вращаться только под прямым углом (90, 180, 270, 360)')
проходить
еще:
# чтение изображения
изображение = cv2. imread(image_path, cv2.IMREAD_GRAYSCALE)
# вращающееся изображение
если угол == 90:
image = np.transpose(image) # транспонирующий массив
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 180:
image = image[::-1, :] # переворачивание строк
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 270:
image = np.transpose(image) # транспонирующий массив
image = image[::-1, :] # переворачивание строк
plt.imshow(изображение, cmap='серый')
еще:
изображение = изображение
plt.imshow(изображение, cmap='серый')
пройти
imread(image_path, cv2.IMREAD_GRAYSCALE)
# вращающееся изображение
если угол == 90:
image = np.transpose(image) # транспонирующий массив
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 180:
image = image[::-1, :] # переворачивание строк
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 270:
image = np.transpose(image) # транспонирующий массив
image = image[::-1, :] # переворачивание строк
plt.imshow(изображение, cmap='серый')
еще:
изображение = изображение
plt.imshow(изображение, cmap='серый')
пройти Используя описанную выше функцию, массивы изображений можно манипулировать таким образом, что их пиксели перестраиваются, чтобы получить повернутые версии исходного изображения.
Результаты, полученные при использовании вышеуказанной функции. Можно также явно изменить значение пикселей в изображении, проиндексировав их и присвоив им новые значения.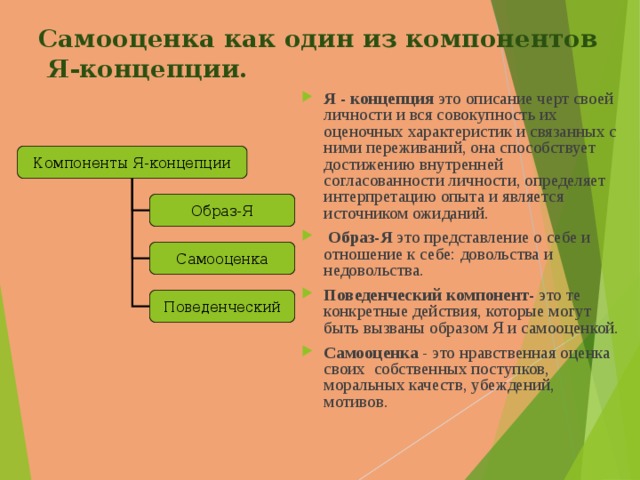 Например, предположим, что мы хотим создать фигуру «Т» из нашей фигуры «J». Это вопрос простого исключения хвоста буквы «J», который формируется пикселями в строке 7, столбцах 2 и 3. Мы можем сделать это, проиндексировав эти пиксели и присвоив им нулевое значение, чтобы они не имели интенсивности.
Например, предположим, что мы хотим создать фигуру «Т» из нашей фигуры «J». Это вопрос простого исключения хвоста буквы «J», который формируется пикселями в строке 7, столбцах 2 и 3. Мы можем сделать это, проиндексировав эти пиксели и присвоив им нулевое значение, чтобы они не имели интенсивности.
# индексация и присвоение image[7, 2:4] = 0
Каналы
Каналы — это свойство изображений, определяющее их цвет. Возвращаясь к трехмерному пространственному представлению, представленному в разделе измерений, для правильного представления изображения необходимо также учитывать ось z. Оказывается, изображение может состоять не только из одного массива, но и из стека массивов. Каждый массив в стеке называется каналом.
Изображения в градациях серого состоят только из одного массива, поэтому они имеют только один канал, как и все массивы, с которыми мы имели дело в предыдущем разделе. С другой стороны, цветные изображения состоят из 3 массивов, наложенных друг на друга, поэтому они имеют 3 канала (9).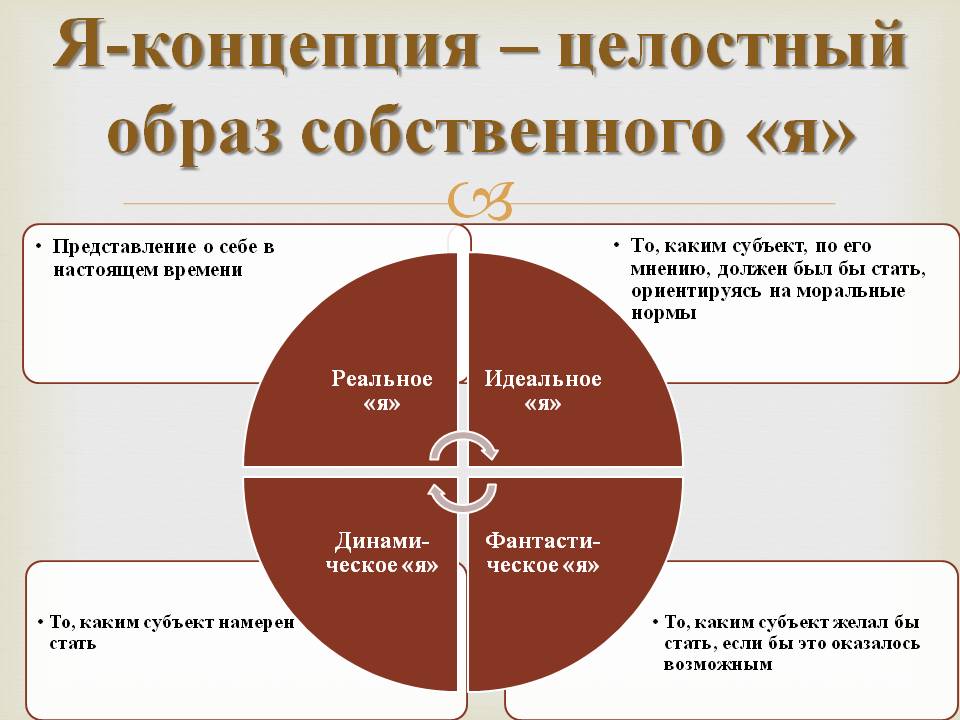 0023 думайте об этих каналах как о листах бумаги, наложенных друг на друга ).
0023 думайте об этих каналах как о листах бумаги, наложенных друг на друга ).
Каналы в цветных изображениях
Каждый канал в цветном изображении представляет собой массив пикселей, которые могут воспроизводить только один из 3 цветов: красный, зеленый, синий (RGB). В каждом цветном изображении эти каналы всегда расположены одинаково: первый — красный, второй — зеленый, а третий — синий.
На основе интенсивности соответствующих пикселей по этим 3 каналам можно сформировать любой цвет. Давайте проверим это, используя фигуру, используя нашу фигуру «J». Мы попробуем создать разные его варианты, каждый вариант будет иметь свой цвет.
J красного цвета поверх черного холста Как сказано в теме, мы пытаемся создать изображение красной фигуры ‘J’ на черном фоне. Чтобы сгенерировать черный фон, нам по существу нужно, чтобы все пиксели фона не имели интенсивности, поэтому значение пикселя равно нулю. Поскольку мы пытаемся создать красную фигуру, только пиксели, очерчивающие фигуру в красном канале, «включаются», пропуская только красный цвет, как показано выше.
# создание изображения размером 9x9 пикселей с 3 каналами изображение = np.zeros((9,9,3)).astype(np.uint8) # включение пикселей, очерчивающих фигуру j в красном канале (канал 0) изображение[1, 2:-2, 0] = 255 изображение[1:-1, 4, 0] = 255 изображение[-2, 2:4, 0] = 255 plt.imshow(image)Зеленый цвет J поверх черного холста
Подобно красной фигуре, полученной выше, для создания зеленой фигуры нам нужно только включить ее очерчивающие пиксели в зеленом канале.
# создание 9изображение x9 пикселей с 3 каналами изображение = np.zeros((9,9,3)).astype(np.uint8) # включение пикселей, очерчивающих фигуру j в зеленом канале (канал 1) изображение[1, 2:-2, 1] = 255 изображение[1:-1, 4, 1] = 255 изображение[-2, 2:4, 1] = 255 plt.imshow(image)Blue Colored J поверх A Black Canvas
Аналогичным образом, для создания синей фигуры на черном фоне включаются только контурные пиксели в синем канале, как показано выше.
# создание изображения 9x9 пикселей с 3 каналами изображение = np.Бирюзовый J поверх бордового холстаzeros((9,9,3)).astype(np.uint8) # включение пикселей, очерчивающих фигуру j в синем канале (канал 2) изображение[1, 2:-2, 2] = 255 изображение[1:-1, 4, 2] = 255 изображение[-2, 2:4, 2] = 255 plt.imshow(image)
Теперь кое-что посложнее. Цель состоит в том, чтобы создать изображение фигуры «J» бирюзового цвета на бордовом фоне. Чтобы создать бордовый фон, бордовые значения RGB (128, 0, 32) должны быть реплицированы по соответствующим каналам для пикселей, составляющих фон.
В том же флюгере для создания бирюзового цвета фигуры «J» бирюзовые значения RGB (0, 128, 128) должны быть назначены контурным пикселям в соответствующих каналах, как показано на изображении выше и воспроизведены в кодовом блоке. ниже.
# создание массива изображение = np.zeros((9,9,3)).astype(np.uint8) # назначение цвета фона в каждом канале изображение[:,:,0] = 128 изображение[:,:,1] = 0 изображение[:,:,2] = 32 # выделение фигуры j в каждом канале изображение[1, 2:-2, 0] = 0 изображение[1, 2:-2, 1] = 128 изображение[1, 2:-2, 2] = 128 изображение[1:-1, 4, 0] = 0 изображение[1:-1, 4, 1] = 128 изображение[1:-1, 4, 2] = 128 изображение[-2, 2:4, 0] = 0 изображение[-2, 2:4, 1] = 128 изображение[-2, 2:4, 2] = 128 plt.imshow(изображение)
Цвет в оттенки серого
Поскольку единственное, что отличает цветные изображения от изображений в градациях серого в цифровом контексте, — это количество каналов, теоретически, если мы сможем найти способ сжать все 3 канала цветного изображения в один канал, мы сможем преобразовать цветные изображения в изображения в градациях серого. Теория работает.
Для этого существует несколько методов, однако самый простой способ — просто взять среднее значение соответствующих пикселей по каналам.
# вычисление среднего значения пикселей по каналам изображение = изображение.среднее (ось = 2)
Изображения в градациях серого В Matplotlib
Как указывалось ранее, изображения в градациях серого (черно-белые) имеют только один канал, подобно одиночным массивам, использованным в предыдущих разделах. Однако при визуализации этих одиночных массивов нам пришлось использовать параметр cmap в Matplotlib. Причина этого заключается в том, что Matplotlib неявно не распознает одноканальные массивы как данные изображения, поэтому они не визуализируются как оттенки серого, а визуализируются как карты цветов.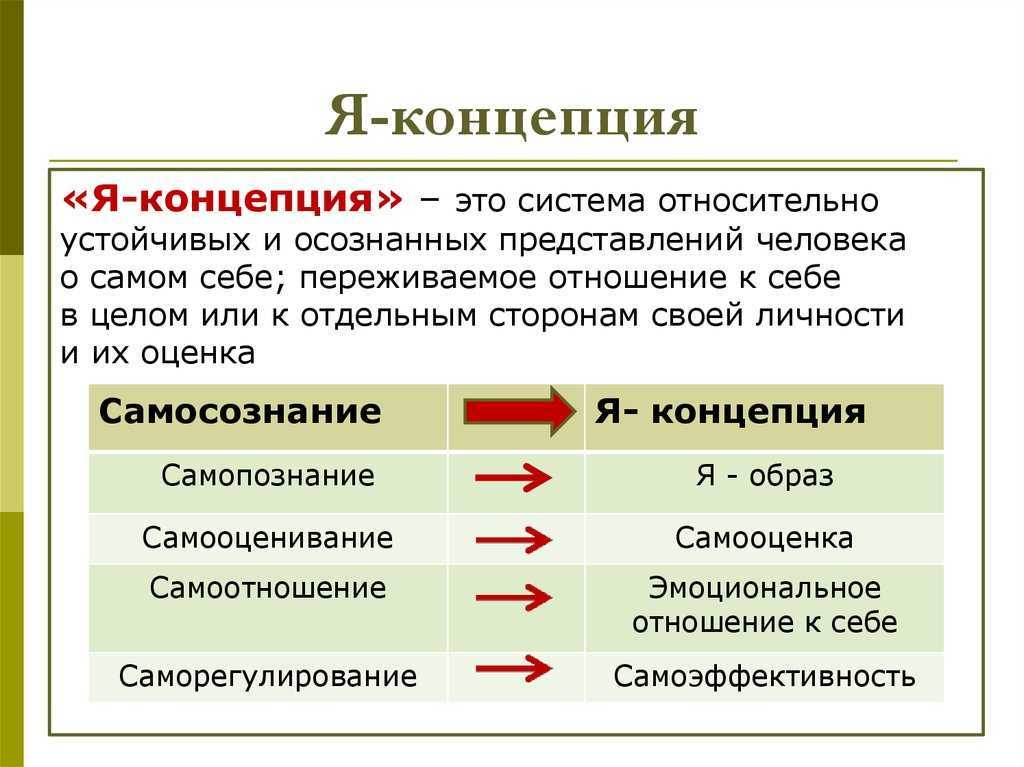
Однако, чтобы создать версию приведенного выше изображения в градациях серого (которое было заархивировано путем установки cmap=’gray’), нам нужно создать трехканальный массив, установить нулевые фоновые пиксели и включить контурные пиксели на каждом канале, чтобы полная интенсивность (255), так как это создаст черный фон и белую фигуру (255, 255, 255).
# создание массива изображение = np.zeros ((9,9,3)) # настройка контура изображение[1, 2:-2,:] = 255 изображение[1:-1, 4,:] = 255 изображение[-2, 2:4,:] = 255 plt.imshow(изображение)
В этой статье мы смогли развить интуитивное представление об основных элементах, составляющих цифровое изображение. Мы перешли от обсуждения измерений, которые служат опорными точками в пространственной структуре, к пикселям, числовым типам, которые формируют изображения, используя их яркость, и, наконец, к каналам, которые помогают формировать цвет, комбинируя различные интенсивности красного, синего и зеленого.
Начало работы
Focus Concept Stok Fotograf, Resimler ve Görseller
Görsel
- Görsel
- Fotoğraf
- İllüstrasyon
- Vektörler
- Video
5.077.359
focus concept stok fotoğraf ve görselini inceleyin veya daha fazla stok fotoğraf ve görsel keşfetmek için yeni bir arama başlatın.Сирала:
En popüler
koyu mavi gökyüzü arka plan üzerinde hedef merkezinde çekim kırmızı dart okları kapatın. i̇ş hedefi veya hedef başarı ve kazanan kavramı. — концепция фокуса сток фото и дизайнKoyu mavi gökyüzü arka plan üzerinde hedef merkezinde çekim kırmız
gün doğumunda halk dürbünü ve dağ siluetleri.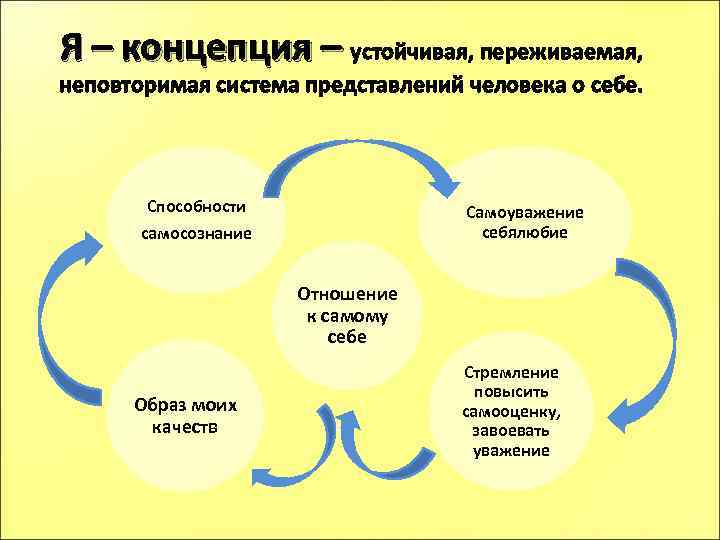 yeni iş kavramları ve yaratıcı fikirler için öngörü ve vizyon. альплер, альгау, бавьера, альманья. — концепция фокуса сток фотографлар ве resimler
yeni iş kavramları ve yaratıcı fikirler için öngörü ve vizyon. альплер, альгау, бавьера, альманья. — концепция фокуса сток фотографлар ве resimlerGün doğumunda halk dürbünü ве Dag Siluetleri. Yeni iş kavramları…
bokeh arka plan ile sanal hedef tahtası ve ok tutan el. i̇ş yatırımı konseptiiçin hedeflerin ve hedeflerin tutulması ve kurulumu. — концепция фокуса сток фото и дизайнBokeh arka plan ile sanal hedef tahtası ve ok tutan el. İş yatırım
mavi arka plan ve kopyalama alanı üzerinde odak iş hedefi için büyüteç camı içinde hedef tahtası. — Концепция фокусировки Stok Fotoğraflar Ve ResimlerMavi Arka Plan Ve Kopyalama alanı üzerinde Odak Iş Hedefi Isicin Büy
OK Birleştirme Odak Arka Planı — Концепция Focus ocloseOK Birleştirme Odak Arka Planı
Ok Hedefe gidior -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor -Fotor. hedefe gidiyor soyut renkli cam arka plan — focus concept сток фото и дизайн
hedefe gidiyor soyut renkli cam arka plan — focus concept сток фото и дизайнSoyut renkli cam arka plan
объектив — концепция фокуса сток фотографлар ве resimlerok hedefe gidiyor — концепт фокус сток фотографлар ве resimlerOk hedefe gidiyor
ofiste toplantı genç yaratıcı iş adamları. — фокус концепции сток фото и resimlerOfiste toplantı genç yaratıcı iş adamları.
i̇zlerken kapatın — focus concept stok fotograflar ve resimlerİzlerken kapatın
tarayın arama konsepti ve fütüristik elektronik teknoloji arka planı ile büyuteç, şeffaf vektör concept stockstrasyon — 9 focus illüteç0002 tarayın arama konsepti ve fütüristik elektronik teknoloji arka… kırmızı dart tahtası ile modern şehir ve gun batımı arka plan hedef ortasına ok isabet. хэдеф иш, элде этмек ве зафер каврамы. — Концепция фокусировки Stok Fotoğraflar Ve ResimlerKırmızı Dart Tahtası Ile Modern şehir ve Gün Batımı Arka Plan …
Gün Başarı Yapmaya Odaklanın — Концепция фокуса Сток Фотогфлар VE -RESIMLER Gün Başryı I.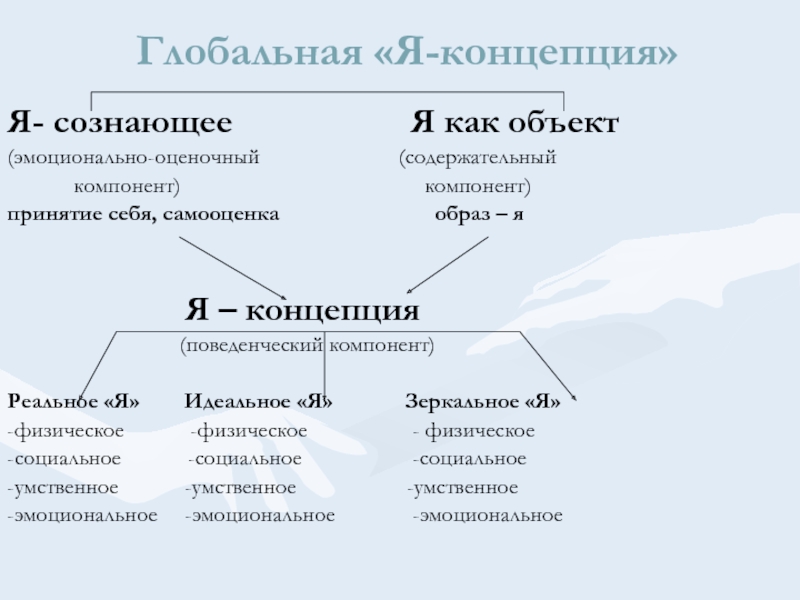

 imshow(изображение, cmap='серый')
imshow(изображение, cmap='серый') 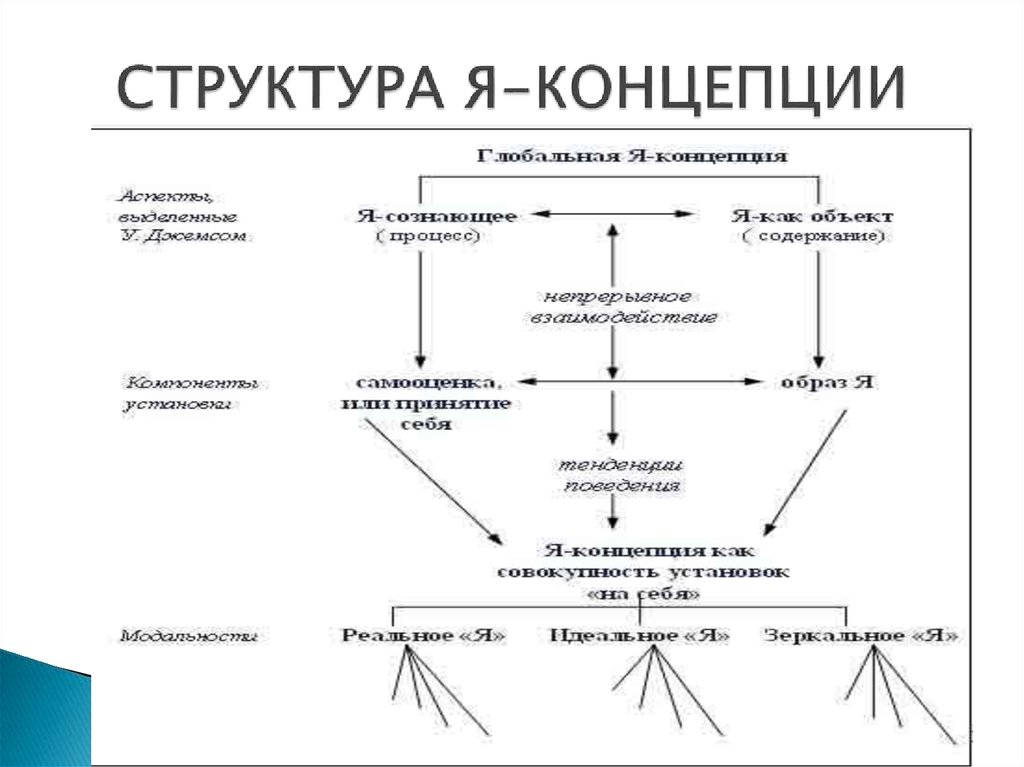 imread(image_path, cv2.IMREAD_GRAYSCALE)
# вращающееся изображение
если угол == 90:
image = np.transpose(image) # транспонирующий массив
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 180:
image = image[::-1, :] # переворачивание строк
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 270:
image = np.transpose(image) # транспонирующий массив
image = image[::-1, :] # переворачивание строк
plt.imshow(изображение, cmap='серый')
еще:
изображение = изображение
plt.imshow(изображение, cmap='серый')
пройти
imread(image_path, cv2.IMREAD_GRAYSCALE)
# вращающееся изображение
если угол == 90:
image = np.transpose(image) # транспонирующий массив
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 180:
image = image[::-1, :] # переворачивание строк
image = image[:, ::-1] # перестановка столбцов
plt.imshow(изображение, cmap='серый')
Элиф угол == 270:
image = np.transpose(image) # транспонирующий массив
image = image[::-1, :] # переворачивание строк
plt.imshow(изображение, cmap='серый')
еще:
изображение = изображение
plt.imshow(изображение, cmap='серый')
пройти  zeros((9,9,3)).astype(np.uint8)
# включение пикселей, очерчивающих фигуру j в синем канале (канал 2)
изображение[1, 2:-2, 2] = 255
изображение[1:-1, 4, 2] = 255
изображение[-2, 2:4, 2] = 255
plt.imshow(image)
zeros((9,9,3)).astype(np.uint8)
# включение пикселей, очерчивающих фигуру j в синем канале (канал 2)
изображение[1, 2:-2, 2] = 255
изображение[1:-1, 4, 2] = 255
изображение[-2, 2:4, 2] = 255
plt.imshow(image)  imshow(изображение)
imshow(изображение)